Unlocking State-Tracking in Linear RNNs Through Negative Eigenvalues

Overview

• Research explores how negative eigenvalues enhance state tracking in Linear RNNs
• Demonstrates LRNNs can maintain oscillatory patterns through negative eigenvalues
• Challenges conventional wisdom about restricting RNNs to positive eigenvalues
• Shows improved performance on sequence modeling tasks

Plain English Explanation

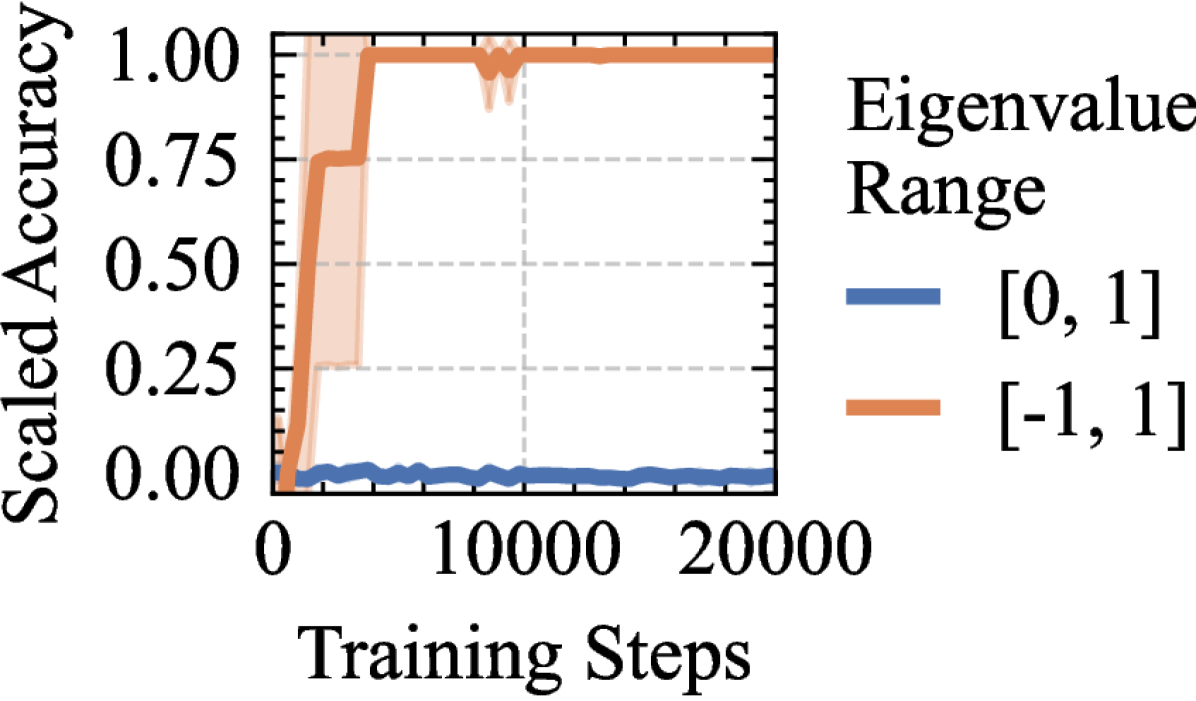
Linear Recurrent Neural Networks (LRNNs) are simple but powerful systems for processing sequences of information. Think of them like a person trying to remember and update information over time. Traditional wisdom suggested these networks work best when they gradually forget information (positive eigenvalues).

This research reveals that allowing LRNNs to have negative patterns of memory (negative eigenvalues) helps them track changing states much better. It's similar to how a pendulum swings back and forth - this oscillating pattern can help the network maintain and process information more effectively.

The team discovered that these oscillating patterns let LRNNs handle complex tasks like keeping track of multiple pieces of information or recognizing patterns in sequences. It's like giving the network the ability to juggle multiple balls instead of just holding onto one.

Key Findings

State tracking capabilities improve significantly when negative eigenvalues are used. The networks showed:

• Better performance on sequence modeling tasks
• Improved ability to maintain multiple state patterns
• More stable long-term memory capabilities
• Enhanced pattern recognition in complex sequences

Technical Explanation

The research implements oscillatory patterns in LRNNs through carefully controlled negative eigenvalues in the recurrent weight matrix. The architecture maintains stability while allowing for periodic state changes.

The experiments tested the networks on various sequence modeling tasks, comparing performance between traditional positive-only eigenvalue systems and those allowing negative values. The results demonstrate that negative eigenvalues enable more sophisticated state tracking mechanisms.

Regular language processing capabilities showed marked improvement, particularly in tasks requiring maintenance of multiple state variables.

Critical Analysis

While the results are promising, several limitations exist:

• The relationship between eigenvalue patterns and specific tasks needs further exploration
• Scaling properties for very long sequences remain unclear
• The impact on training stability requires additional investigation
• Potential trade-offs between oscillatory behavior and memory persistence

Conclusion

This work fundamentally changes our understanding of how LRNNs can process information. The inclusion of negative eigenvalues opens new possibilities for sequence modeling applications and suggests that simpler architectures might be more capable than previously thought. This could lead to more efficient and effective neural network designs for sequence processing tasks.