diff --git "a/markdown/unit1/01_introduction_to_diffusers_CN.md" "b/markdown/unit1/01_introduction_to_diffusers_CN.md"
new file mode 100644--- /dev/null
+++ "b/markdown/unit1/01_introduction_to_diffusers_CN.md"
@@ -0,0 +1,882 @@
+# 🤗 Diffusers 介绍
+
+
+
+在这个 Notebook 里,你将训练你的第一个扩散模型来 **生成美丽的蝴蝶的图片 🦋**。在此过程中,你将了解 🤗 Diffuers 库,它将为我们稍后将在课程中介绍的更高级的应用程序提供良好的基础
+
+让我们开始吧!
+
+## 你将学习到
+
+在这个 Notebook 中,你将:
+
+- 看到一个强大的自定义扩散模型管道 (并了解到如何制作一个自己的版本)
+- 通过以下方式创建你自己的迷你管道:
+- 回顾扩散模型背后的核心思想
+- 从 Hub 中加载数据进行训练
+- 探索如何使用 scheduler 将噪声添加到数据中
+- 创建和训练一个 UNet 模型
+- 将各个组件拼装在一起来形成一个工作管道 (working pipelines)
+- 编辑并运行一个脚本,用于初始化一个较长的训练,该脚本将处理
+- 使用 Accelerate 来进行多 GPU 加速训练
+- 实验日志记录以跟踪关键统计数据
+- 将最终的模型上传到 Hugging Face Hub
+
+❓如果你有任何问题,请发布在 Hugging Face 的 Discord 服务器`#diffusion-models-class`频道中。你可以在这里完成注册: https://huggingface.co/join/discord
+
+## 预备知识
+
+在进入 Notebook 之前,你需要:
+
+* 📖 阅读第一单元的材料
+* 🤗 在 Hugging Face Hub 上创建一个账户。你可以在这里完成注册: https://huggingface.co/join
+
+## 步骤 1: 设置
+
+运行以下单元以安装 diffusers 库以及一些其他要求:
+
+
+```python
+%pip install -qq -U diffusers datasets transformers accelerate ftfy pyarrow
+```
+
+接下来,请前往 https://huggingface.co/settings/tokens 创建具有写权限的访问令牌:
+
+
+
+你可以使用命令行来通过此令牌登录 (`huggingface-cli login`) 或者运行以下单元来登录:
+
+
+```python
+from huggingface_hub import notebook_login
+
+notebook_login()
+```
+
+ Login successful
+ Your token has been saved to /root/.huggingface/token
+
+
+然后你需要安装 Git LFS 来上传模型检查点:
+
+
+```python
+%%capture
+!sudo apt -qq install git-lfs
+!git config --global credential.helper store
+```
+
+最后,让我们导入将要使用的库,并定义一些方便函数,稍后我们将会在 Notebook 中使用这些函数:
+
+
+```python
+import numpy as np
+import torch
+import torch.nn.functional as F
+from matplotlib import pyplot as plt
+from PIL import Image
+
+
+def show_images(x):
+ """Given a batch of images x, make a grid and convert to PIL"""
+ x = x * 0.5 + 0.5 # Map from (-1, 1) back to (0, 1)
+ grid = torchvision.utils.make_grid(x)
+ grid_im = grid.detach().cpu().permute(1, 2, 0).clip(0, 1) * 255
+ grid_im = Image.fromarray(np.array(grid_im).astype(np.uint8))
+ return grid_im
+
+
+def make_grid(images, size=64):
+ """Given a list of PIL images, stack them together into a line for easy viewing"""
+ output_im = Image.new("RGB", (size * len(images), size))
+ for i, im in enumerate(images):
+ output_im.paste(im.resize((size, size)), (i * size, 0))
+ return output_im
+
+
+# Mac users may need device = 'mps' (untested)
+device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
+```
+
+好了,我们都准备好了!
+
+## Dreambooth:即将到来的巅峰
+
+如果你在过去几个月里看过人工智能相关的社交媒体,你就会听说过 Stable Diffusion 模型。这是一个强大的文本条件隐式扩散模型(别担心,我们将会学习这些概念)。但它有一个缺点:它不知道你或我长什么样,除非我们足够出名以至于互联网上发布我们的照片。
+
+Dreambooth 允许我们创建自己的模型变体,并对特定的面部、对象或样式有一些额外的了解。Corridor Crew 制作了一段出色的视频,用一致的任务形象来讲故事,这是一个很好的说明了这种技术的能力的例子:
+
+
+```python
+from IPython.display import YouTubeVideo
+
+YouTubeVideo("W4Mcuh38wyM")
+```
+
+
+
+
+
+
+
+
+
+
+这是一个使用了 [这个模型](https://huggingface.co/sd-dreambooth-library/mr-potato-head) 的例子。该模型的训练使用了 5 张著名的儿童玩具 "Mr Potato Head"的照片。
+
+首先,让我们来加载这个管道。这些代码会自动从 Hub 下载模型权重等需要的文件。由于这个只有一行的 demo 需要下载数 GB 的数据,因此你可以跳过此单元格,只需欣赏样例输出即可!
+
+
+```python
+from diffusers import StableDiffusionPipeline
+
+# Check out https://huggingface.co/sd-dreambooth-library for loads of models from the community
+model_id = "sd-dreambooth-library/mr-potato-head"
+
+# Load the pipeline
+pipe = StableDiffusionPipeline.from_pretrained(model_id, torch_dtype=torch.float16).to(
+ device
+)
+```
+
+
+ Fetching 15 files: 0%| | 0/15 [00:00
+
+$q (\mathbf {x}_t \vert \mathbf {x}_{t-1}) = \mathcal {N}(\mathbf {x}_t; \sqrt {1 - \beta_t} \mathbf {x}_{t-1}, \beta_t\mathbf {I}) \quad
+q (\mathbf {x}_{1:T} \vert \mathbf {x}_0) = \prod^T_{t=1} q (\mathbf {x}_t \vert \mathbf {x}_{t-1})$
+
+
+这就是说,我们取 $x_{t-1}$, 给他一个 $\sqrt {1 - \beta_t}$ 的系数,然后加上带有 $\beta_t$ 系数的噪声。 这里 $\beta$ 是根据一些管理器来为每一个 t 设定的,来决定每一个迭代周期中添加多少噪声。 现在,我们不想把这个推演进行 500 次来得到 $x_{500}$,所以我们用另一个公式来���据给出的 $x_0$ 计算得到任意 t 时刻的 $x_t$:
+
+$\begin {aligned}
+q (\mathbf {x}_t \vert \mathbf {x}_0) &= \mathcal {N}(\mathbf {x}_t; \sqrt {\bar {\alpha}_t} \mathbf {x}_0, {(1 - \bar {\alpha}_t)} \mathbf {I})
+\end {aligned}$ where $\bar {\alpha}_t = \prod_{i=1}^T \alpha_i$ and $\alpha_i = 1-\beta_i$
+
+数学符号看起来总是很可怕!好在有管理器来为我们完成这些运算。我们可以画出 $\sqrt {\bar {\alpha}_t}$ (标记为`sqrt_alpha_prod`) 和 $\sqrt {(1 - \bar {\alpha}_t)}$ (标记为`sqrt_one_minus_alpha_prod`) 来看一下输入 (x) 与噪声是如何在不同迭代周期中量化和叠加的:
+
+
+```python
+plt.plot(noise_scheduler.alphas_cumprod.cpu() ** 0.5, label=r"${\sqrt{\bar{\alpha}_t}}$")
+plt.plot((1 - noise_scheduler.alphas_cumprod.cpu()) ** 0.5, label=r"$\sqrt{(1 - \bar{\alpha}_t)}$")
+plt.legend(fontsize="x-large");
+```
+
+**练习:** 你可以探索一下使用不同的 beta_start 时曲线是如何变化的,beta_end 与 beta_schedule 可以通过以下注释内容来修改:
+
+
+```python
+# One with too little noise added:
+# noise_scheduler = DDPMScheduler(num_train_timesteps=1000, beta_start=0.001, beta_end=0.004)
+# The 'cosine' schedule, which may be better for small image sizes:
+# noise_scheduler = DDPMScheduler(num_train_timesteps=1000, beta_schedule='squaredcos_cap_v2')
+```
+
+不论你选择了哪一个管理器 (调度器),我们现在都可以使用`noise_scheduler.add_noise`功能来添加不同程度的噪声,就像这样:
+
+
+```python
+timesteps = torch.linspace(0, 999, 8).long().to(device)
+noise = torch.randn_like(xb)
+noisy_xb = noise_scheduler.add_noise(xb, noise, timesteps)
+print("Noisy X shape", noisy_xb.shape)
+show_images(noisy_xb).resize((8 * 64, 64), resample=Image.NEAREST)
+```
+
+ Noisy X shape torch.Size ([8, 3, 32, 32])
+
+
+
+
+
+
+
+
+
+
+
+再来,在这里探索使用这里不同噪声管理器和预设参数带来的效果。 [This video](https://www.youtube.com/watch?v=fbLgFrlTnGU) 这个视频很好的解释了一些上述数学运算的细节,同时也是对此类概念的一个很好引入介绍。
+
+## 步骤 4:定义模型
+
+现在我们来到了核心部分:模型本身。
+
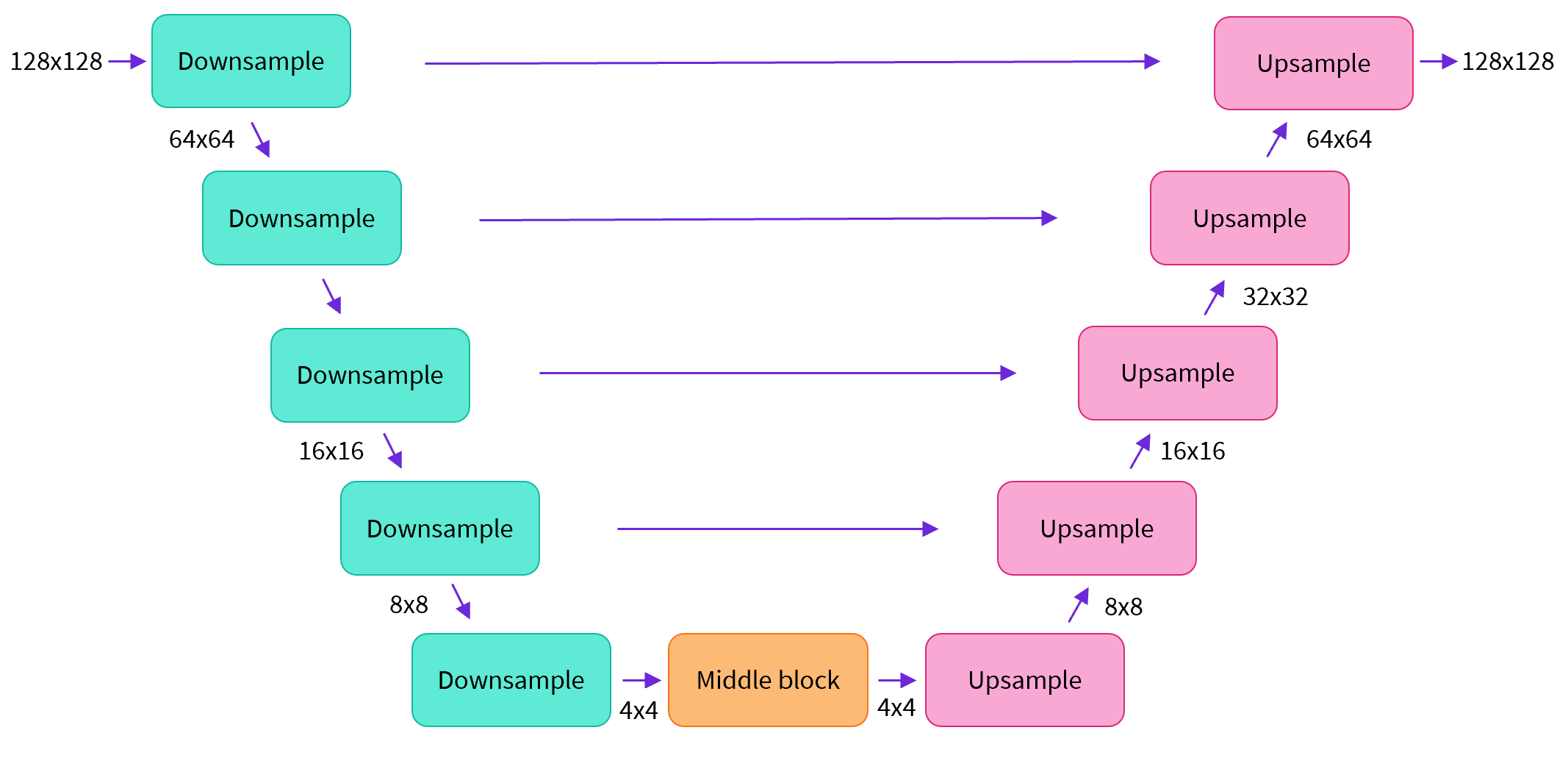
+大多数扩散模型使用的模型结构都是一些 [U-net] 的变形 (https://arxiv.org/abs/1505.04597) 也是我们在这里会用到的结构。
+
+
+
+概括来说:
+- 输入模型中的图片经过几个由 ResNetLayer 构成的层,其中每层都使图片尺寸减半。
+- 之后在经过同样数量的层把图片升采样。
+- 其中还有对特征在相同位置的上、下采样层残差连接模块。
+
+模型一个关键特征既是,输出图片尺寸与输入图片相同,这正是我们这里需要的。
+
+Diffusers 为我们提供了一个易用的`UNet2DModel`类,用来在 PyTorch 创建所需要的结构。
+
+我们来使用 U-net 为我们生成目标大小的图片吧。
+注意这里`down_block_types`对应下采样模块 (上图中绿色部分), 而`up_block_types`对应上采样模块 (上图中红色部分):
+
+
+```python
+from diffusers import UNet2DModel
+
+# Create a model
+model = UNet2DModel(
+ sample_size=image_size, # the target image resolution
+ in_channels=3, # the number of input channels, 3 for RGB images
+ out_channels=3, # the number of output channels
+ layers_per_block=2, # how many ResNet layers to use per UNet block
+ block_out_channels=(64, 128, 128, 256), # More channels -> more parameters
+ down_block_types=(
+ "DownBlock2D", # a regular ResNet downsampling block
+ "DownBlock2D",
+ "AttnDownBlock2D", # a ResNet downsampling block with spatial self-attention
+ "AttnDownBlock2D",
+ ),
+ up_block_types=(
+ "AttnUpBlock2D",
+ "AttnUpBlock2D", # a ResNet upsampling block with spatial self-attention
+ "UpBlock2D",
+ "UpBlock2D", # a regular ResNet upsampling block
+ ),
+)
+model.to(device);
+```
+
+当在处理更高分辨率的输入时,你可能想用更多层的下、上采样模块,让注意力层只聚焦在最低分辨率(最底)层来减少内存消耗。我们在之后会讨论该如何实验来找到最适用与你手头场景的配置方法。
+
+我们可以通过输入一批数据和随机的迭代周期数来看输出是否与输入尺寸相同:
+
+
+```python
+with torch.no_grad():
+ model_prediction = model(noisy_xb, timesteps).sample
+model_prediction.shape
+```
+
+
+
+
+ torch.Size ([8, 3, 32, 32])
+
+
+
+在下一步中,我们来看如何训练这个模型。
+
+## 步骤 5:创建训练循环
+
+终于可以训练了!下面这是 PyTorch 中经典的优化迭代循环,在这里一批一批的送入数据然后通过优化器来一步步更新模型参数 - 在这个样例中我们使用学习率为 0.0004 的 AdamW 优化器。
+
+对于每一批的数据,我们要
+- 随机取样几个迭代周期
+- 根据预设为数据加入噪声
+- 把带噪数据送入模型
+- 使用 MSE 作为损失函数来比较目标结果与模型预测结果(在这里是加入噪声的场景)
+- 通过`loss.backward ()`与`optimizer.step ()`来更新模型参数
+
+在这个过程中我们记录 Loss 值用来后续的绘图。
+
+NB: 这段代码大概需 10 分钟来运行 - 你也可以跳过以下两块操作直接使用预训练好的模型。供你选择,你可以探索下通过缩小模型层中的通道数会对运行速度有多少提升。
+
+官方扩散模型示例 [official diffusers training example](https://colab.research.google.com/github/huggingface/notebooks/blob/main/diffusers/training_example.ipynb) 训练了在更高分辨率数据集上的一个更大的模型,这也是一个极为精简训练循环的优秀示例:
+
+
+```python
+# Set the noise scheduler
+noise_scheduler = DDPMScheduler(
+ num_train_timesteps=1000, beta_schedule="squaredcos_cap_v2"
+)
+
+# Training loop
+optimizer = torch.optim.AdamW(model.parameters(), lr=4e-4)
+
+losses = []
+
+for epoch in range(30):
+ for step, batch in enumerate(train_dataloader):
+ clean_images = batch["images"].to(device)
+ # Sample noise to add to the images
+ noise = torch.randn(clean_images.shape).to(clean_images.device)
+ bs = clean_images.shape[0]
+
+ # Sample a random timestep for each image
+ timesteps = torch.randint(
+ 0, noise_scheduler.num_train_timesteps, (bs,), device=clean_images.device
+ ).long()
+
+ # Add noise to the clean images according to the noise magnitude at each timestep
+ noisy_images = noise_scheduler.add_noise(clean_images, noise, timesteps)
+
+ # Get the model prediction
+ noise_pred = model(noisy_images, timesteps, return_dict=False)[0]
+
+ # Calculate the loss
+ loss = F.mse_loss(noise_pred, noise)
+ loss.backward(loss)
+ losses.append(loss.item())
+
+ # Update the model parameters with the optimizer
+ optimizer.step()
+ optimizer.zero_grad()
+
+ if (epoch + 1) % 5 == 0:
+ loss_last_epoch = sum(losses[-len(train_dataloader) :]) / len(train_dataloader)
+ print(f"Epoch:{epoch+1}, loss: {loss_last_epoch}")
+```
+
+ Epoch:5, loss: 0.16273280512541533
+ Epoch:10, loss: 0.11161588924005628
+ Epoch:15, loss: 0.10206522420048714
+ Epoch:20, loss: 0.08302505919709802
+ Epoch:25, loss: 0.07805309211835265
+ Epoch:30, loss: 0.07474562455900013
+
+
+绘制 loss 曲线,我们能看到模型在一开始快速的收敛,接下来以一个较慢的速度持续优化(我们用右边 log 坐标轴的视图可以看的更清楚):
+
+
+```python
+fig, axs = plt.subplots(1, 2, figsize=(12, 4))
+axs[0].plot(losses)
+axs[1].plot(np.log(losses))
+plt.show()
+```
+
+
+
+
+ []
+
+
+
+
+
+
+
+
+
+你可以选择运行上面的代码,也可以这样通过管道来调用模型:
+
+
+```python
+# Uncomment to instead load the model I trained earlier:
+# model = butterfly_pipeline.unet
+```
+
+## 步骤 6:生成图像
+
+我们怎么从这个模型中得到图像呢?
+
+### 方法 1:建立一个管道:
+
+
+```python
+from diffusers import DDPMPipeline
+
+image_pipe = DDPMPipeline(unet=model, scheduler=noise_scheduler)
+```
+
+
+```python
+pipeline_output = image_pipe()
+pipeline_output.images[0]
+```
+
+
+ 0%| | 0/1000 [00:00