repo
stringlengths 26
115
| file
stringlengths 54
212
| language
stringclasses 2
values | license
stringclasses 16
values | content
stringlengths 19
1.07M
|
|---|---|---|---|---|
https://github.com/ohmycloud/computer-science-notes | https://raw.githubusercontent.com/ohmycloud/computer-science-notes/main/Misc/iec104-DLT634.5101.typ | typst | #import "@preview/tablex:0.0.7": tablex, cellx, rowspanx, colspanx
== 7.3.1 在监视方向过程信息的应用服务数据单元
== 7.3.1.1 类型标识 1 : M_SP_NA_1
不带时标的单点信息
信息对象序列(SQ = 0)
#tablex(
columns: 10,
align: center + horizon,
stroke: (thickness: 0.3pt, paint: black),
[0], [0], [0], [0], [0], [0], [0], [1], [类型标识 (TYP)], rowspanx(4)[数据单元标识符#linebreak()在 7.1 中定义],
[0], colspanx(7)[信息元素数 i], [可变结构限定词 (VSQ)], (),
colspanx(8)[在 7.2.3 中定义], [传送原因 (COT)], (),
colspanx(8)[在 7.2.4 中定义], [应用服务数据单元公共地址], (),
colspanx(8)[在 7.2.5 中定义], [信息对象地址], rowspanx(2)[信息对象 1],
[IV], [NT], [SB], [BL], [0], [0], [0], [SP1], [SIQ=带品质描述词的单点信息(在 7.2.6.1 中定义)], (),
colspanx(8)[…], […], [],
colspanx(8)[在 7.2.5 中定义], [信息对象地址], rowspanx(2)[信息对象 i],
[IV], [NT], [SB], [BL], [0], [0], [0], [SP1], [SIQ=带品质描述词的单点信息(在 7.2.6.1 中定义)], ()
)
单个信息对象中顺序的信息元素(SQ = 1)
#tablex(
columns: 10,
align: center + horizon,
stroke: (thickness: 0.3pt, paint: black),
[0], [0], [0], [0], [0], [0], [0], [1], [类型标识 (TYP)], rowspanx(4)[数据单元标识符#linebreak()在 7.1 中定义],
[1], colspanx(7)[信息元素数 j], [可变结构限定词 (VSQ)], (),
colspanx(8)[在 7.2.3 中定义], [传送原因 (COT)], (),
colspanx(8)[在 7.2.4 中定义], [应用服务数据单元公共地址], (),
colspanx(8)[在 7.2.5 中定义], [信息对象地址 A], rowspanx(4)[信息对象],
[IV], [NT], [SB], [BL], [0], [0], [0], [SP1], [SIQ=带品质描述词的单点信息(在 7.2.6.1 中定义)#linebreak()属于信息对象地址 A], (),
colspanx(8)[…], […], (),
[IV], [NT], [SB], [BL], [0], [0], [0], [SP1], [SIQ=带品质描述词的单点信息(在 7.2.6.1 中定义)#linebreak()属于信息对象地址 A+j-1], ()
)
== 7.3.1.2 类型标识 2 : M_SP_TA_1
带时标的单点信息
信息对象序列(SQ = 0)
#tablex(
columns: 10,
align: center + horizon,
stroke: (thickness: 0.3pt, paint: black),
[0], [0], [0], [0], [0], [0], [1], [0], [类型标识 (TYP)], rowspanx(4)[数据单元标识符#linebreak()在 7.1 中定义],
[0], colspanx(7)[信息对象数 i], [可变结构限定词 (VSQ)], (),
colspanx(8)[在 7.2.3 中定义], [传送原因 (COT)], (),
colspanx(8)[在 7.2.4 中定义], [应用服务数据单元公共地址], (),
colspanx(8)[在 7.2.5 中定义], [信息对象地址], rowspanx(3)[信息对象 1],
[IV], [NT], [SB], [BL], [0], [0], [0], [SP1], [SIQ=带品质描述词的单点信息(在 7.2.6.1 中定义)], (),
colspanx(8)[CP24Time2a 在 7.2.6.19 中定义], [三个八位位组二进制时间], (),
colspanx(8)[...], [...], [],
colspanx(8)[在 7.2.5 中定义], [信息对象地址], rowspanx(3)[信息对象 i],
[IV], [NT], [SB], [BL], [0], [0], [0], [SP1], [SIQ=带品质描述词的单点信息(在 7.2.6.1 中定义)], (),
colspanx(8)[CP24Time2a 在 7.2.6.19 中定义], [三个八位位组二进制时间], (),
)
=== 7.3.1.3 类型标识 3 : M_DP_NA_1
不带时标的双点信息
信息对象序列(SQ = 0)
#tablex(
columns: 10,
align: center + horizon,
stroke: (thickness: 0.3pt, paint: black),
[0], [0], [0], [0], [0], [0], [1], [1], [类型标识 (TYP)], rowspanx(4)[数据单元标识符#linebreak()在 7.1 中定义],
[0], colspanx(7)[信息对象数 i], [可变结构限定词 (VSQ)], (),
colspanx(8)[在 7.2.3 中定义], [传送原因 (COT)], (),
colspanx(8)[在 7.2.4 中定义], [应用服务数据单元公共地址], (),
colspanx(8)[在 7.2.5 中定义], [信息对象地址], rowspanx(2)[信息对象 1],
[IV], [NT], [SB], [BL], [0], [0], [], [DPI], [SIQ=带品质描述词的双点信息(在 7.2.6.2 中定义)], (),
colspanx(8)[...], [...], [],
colspanx(8)[在 7.2.5 中定义], [信息对象地址], rowspanx(2)[信息对象 i],
[IV], [NT], [SB], [BL], [0], [0], [], [DPI], [DIQ=带品质描述词的双点信息(在 7.2.6.2 中定义)], ()
)
单个信息对象中顺序的信息元素(SQ = 1)
#tablex(
columns: 10,
align: center + horizon,
stroke: (thickness: 0.3pt, paint: black),
[0], [0], [0], [0], [0], [0], [1], [1], [类型标识 (TYP)], rowspanx(4)[数据单元标识符#linebreak()在 7.1 中定义],
[1], colspanx(7)[信息对象数 i], [可变结构限定词 (VSQ)], (),
colspanx(8)[在 7.2.3 中定义], [传送原因 (COT)], (),
colspanx(8)[在 7.2.4 中定义], [应用服务数据单元公共地址], (),
colspanx(8)[在 7.2.5 中定义], [信息对象地址], rowspanx(4)[信息对象],
[IV], [NT], [SB], [BL], [0], [0], [], [DPI], [1 DIQ=带品质描述词的双点信息(在 7.2.6.2 中定义)#linebreak()属于信息对象地址 A], (),
colspanx(8)[...], [...], (),
[IV], [NT], [SB], [BL], [0], [0], [], [DPI], [j DIQ=带品质描述词的双点信息(在 7.2.6.2 中定义)#linebreak()属于信息对象地址 A+j-1], ()
)
== 7.3.1.4 类型标识 4 : M_DP_TA_1
带时标的双点信息(SQ = 0)
信息对象序列(SQ = 0)
#tablex(
columns: 10,
align: center + horizon,
stroke: (thickness: 0.3pt, paint: black),
[0], [0], [0], [0], [0], [1], [0], [0], [类型标识 (TYP)], rowspanx(4)[数据单元标识符#linebreak()在 7.1 中定义],
[0], colspanx(7)[信息对象数 i], [可变结构限定词 (VSQ)], (),
colspanx(8)[在 7.2.3 中定义], [传送原因 (COT)], (),
colspanx(8)[在 7.2.4 中定义], [应用服务数据单元公共地址], (),
colspanx(8)[在 7.2.5 中定义], [信息对象地址], rowspanx(2)[信息对象 1],
[IV], [NT], [SB], [BL], [0], [0], [], [DPI], [DIQ=带品质描述词的双点信息(在 7.2.6.2 中定义)], (),
colspanx(8)[CP24Time2a 在 7.2.6.19 中定义], [三个八位位组二进制时间], [],
colspanx(8)[...], [...], [],
colspanx(8)[在 7.2.5 中定义], [信息对象地址], rowspanx(3)[信息对象 i],
[IV], [NT], [SB], [BL], [0], [0], [], [DPI], [DIQ=带品质描述词的双点信息(在 7.2.6.2 中定义)], (),
colspanx(8)[CP24Time2a 在 7.2.6.19 中定义], [三个八位位组二进制时间], ()
)
== 7.3.1.5 类型标识 5 : M_ST_NA_1
不带时标的步位置信息
信息对象序列(SQ = 0)
== 7.3.2 在控制方向过程信息的应用服务数据单元
== 7.3.2.1 类型标识 45 : C_SC_NA_1
单命令
单个信息对象(SQ = 0)
#tablex(
columns: 10,
align: center + horizon,
stroke: (thickness: 0.3pt, paint: black),
[0], [0], [1], [0], [1], [1], [0], [1], [类型标识 (TYP)], rowspanx(4)[数据单元标识符#linebreak()在 7.1 中定义],
[0], [0], [0], [0], [0], [0], [0], [1], [可变结构限定词 (VSQ)], (),
colspanx(8)[在 7.2.3 中定义], [传送原因 (COT)], (),
colspanx(8)[在 7.2.4 中定义], [应用服务数据单元公共地址], (),
colspanx(8)[在 7.2.5 中定义], [信息对象地址], rowspanx(2)[信息对象],
colspanx(2)[S/E], colspanx(4)[QU], [0], [SCS], [SCO=单命令(在 7.2.6.15 中定义)], ()
)
== 7.3.2.2 类型标识 46 : C_DC_NA_1
双命令
单个信息对象(SQ = 0)
#tablex(
columns: 10,
align: center + horizon,
stroke: (thickness: 0.3pt, paint: black),
[0], [0], [1], [0], [1], [1], [1], [0], [类型标识 (TYP)], rowspanx(4)[数据单元标识符#linebreak()在 7.1 中定义],
[0], [0], [0], [0], [0], [0], [0], [1], [可变结构限定词 (VSQ)], (),
colspanx(8)[在 7.2.3 中定义], [传送原因 (COT)], (),
colspanx(8)[在 7.2.4 中定义], [应用服务数据单元公共地址], (),
colspanx(8)[在 7.2.5 中定义], [信息对象地址], rowspanx(2)[信息对象],
colspanx(2)[S/E], colspanx(4)[QU], [0], [DCS], [DCO=双命令(在 7.2.6.16 中定义)], ()
)
== 7.3.2.3 类型标识 47 : C_RC_NA_1
步调节命令
单个信息对象(SQ = 0)
#tablex(
columns: 10,
align: center + horizon,
stroke: (thickness: 0.3pt, paint: black),
[0], [0], [1], [0], [1], [1], [1], [1], [类型标识 (TYP)], rowspanx(4)[数据单元标识符#linebreak()在 7.1 中定义],
[0], [0], [0], [0], [0], [0], [0], [1], [可变结构限定词 (VSQ)], (),
colspanx(8)[在 7.2.3 中定义], [传送原因 (COT)], (),
colspanx(8)[在 7.2.4 中定义], [应用服务数据单元公共地址], (),
colspanx(8)[在 7.2.5 中定义], [信息对象地址], rowspanx(2)[信息对象],
colspanx(2)[S/E], colspanx(4)[QU], colspanx(2)[RCS], [RCO=步调节命令(在 7.2.6.17 中定义)], ()
)
== 7.3.2.4 类型标识 48 : C_SE_NA_1
设定命令, 归一化值
单个信息对象(SQ = 0)
#tablex(
columns: 10,
align: center + horizon,
stroke: (thickness: 0.3pt, paint: black),
[0], [0], [1], [1], [0], [0], [0], [0], [类型标识 (TYP)], rowspanx(4)[数据单元标识符#linebreak()在 7.1 中定义],
[0], [0], [0], [0], [0], [0], [0], [1], [可变结构限定词 (VSQ)], (),
colspanx(8)[在 7.2.3 中定义], [传送原因 (COT)], (),
colspanx(8)[在 7.2.4 中定义], [应用服务数据单元公共地址], (),
colspanx(8)[在 7.2.5 中定义], [信息对象地址], rowspanx(4)[信息对象],
colspanx(8)[值], rowspanx(2)[NVA=标度化值(在 7.2.6.6 中定义)], (),
[S], colspanx(7)[值], (), (),
[S/E], colspanx(7)[QL], [QOS=设定命令限定词(在 7.2.6.39 中定义)], ()
)
== 7.3.2.5 类型标识 49 : C_SE_NB_1
设定命令, 标度化值
单个信息对象(SQ = 0)
#tablex(
columns: 10,
align: center + horizon,
stroke: (thickness: 0.3pt, paint: black),
[0], [0], [1], [1], [0], [0], [0], [1], [类型标识 (TYP)], rowspanx(4)[数据单元标识符#linebreak()在 7.1 中定义],
[0], [0], [0], [0], [0], [0], [0], [1], [可变结构限定词 (VSQ)], (),
colspanx(8)[在 7.2.3 中定义], [传送原因 (COT)], (),
colspanx(8)[在 7.2.4 中定义], [应用服务数据单元公共地址], (),
colspanx(8)[在 7.2.5 中定义], [信息对象地址], rowspanx(4)[信息对象],
colspanx(8)[值], rowspanx(2)[SVA=标度化值(在 7.2.6.7 中定义)], (),
[S], colspanx(7)[值], (), (),
[S/E], colspanx(7)[QL], [QOS=设定命令限定词(在 7.2.6.39 中定义)], ()
)
== 7.3.2.6 类型标识 50 : C_SE_NC_1
设定命令, 短浮点数
单个信息对象(SQ = 0)
#tablex(
columns: 10,
align: center + horizon,
stroke: (thickness: 0.3pt, paint: black),
[0], [0], [1], [1], [0], [0], [1], [0], [类型标识 (TYP)], rowspanx(4)[数据单元标识符#linebreak()在 7.1 中定义],
[0], [0], [0], [0], [0], [0], [0], [1], [可变结构限定词 (VSQ)], (),
colspanx(8)[在 7.2.3 中定义], [传送原因 (COT)], (),
colspanx(8)[在 7.2.4 中定义], [应用服务数据单元公共地址], (),
colspanx(8)[在 7.2.5 中定义], [信息对象地址], rowspanx(5)[信息对象],
colspanx(8)[小数], rowspanx(4)[IEEE STD 754 短浮点数(在 7.2.6.8 中定义)], (),
colspanx(8)[小数], (), (),
[E], colspanx(7)[小数], (), (),
[S], colspanx(7)[指数], (), (),
[S/E], colspanx(7)[QL], [QOS=设定命令限定词(在 7.2.6.39 中定义)], ()
)
== 7.3.2.7 类型标识 51 : C_BO_NA_1
32 比特串
单个信息对象(SQ = 0)
#tablex(
columns: 10,
align: center + horizon,
stroke: (thickness: 0.3pt, paint: black),
[0], [0], [1], [1], [0], [0], [1], [1], [类型标识 (TYP)], rowspanx(4)[数据单元标识符#linebreak()在 7.1 中定义],
[0], [0], [0], [0], [0], [0], [0], [1], [可变结构限定词 (VSQ)], (),
colspanx(8)[在 7.2.3 中定义], [传送原因 (COT)], (),
colspanx(8)[在 7.2.4 中定义], [应用服务数据单元公共地址], (),
colspanx(8)[在 7.2.5 中定义], [信息对象地址], rowspanx(5)[信息对象],
colspanx(8)[比特串], rowspanx(4)[BSI=二进制状态信息, 32bit(在 7.2.6.13 中定义)], (),
colspanx(8)[比特串], (), (),
colspanx(8)[比特串], (), (),
colspanx(8)[比特串], (), ()
)
== 7.3.3 在监视方向系统信息的应用服务数据单元
类型标识 70 : M_EI_NA_1
初始化结束
单个信息对象(SQ = 0)
#tablex(
columns: 10,
align: center + horizon,
stroke: (thickness: 0.3pt, paint: black),
[0], [1], [0], [0], [0], [1], [1], [0], [类型标识 (TYP)], rowspanx(4)[数据单元标识符#linebreak()在 7.1 中定义],
[0], [0], [0], [0], [0], [0], [0], [1], [可变结构限定词 (VSQ)], (),
colspanx(8)[在 7.2.3 中定义], [传送原因 (COT)], (),
colspanx(8)[在 7.2.4 中定义], [应用服务数据单元公共地址], (),
colspanx(8)[在 7.2.5 中定义], [信息对象地址=0], rowspanx(2)[信息对象],
colspanx(8)[CP8], [COI=初始化原因(在 7.2.6.21 中定义)], ()
)
== 7.3.4 在控制方向系统信息的应用服务数据单元
== 7.3.4.1 类型标识 100 : C_IC_NA_1
召唤命令
单个信息对象(SQ = 0)
#tablex(
columns: 10,
align: center + horizon,
stroke: (thickness: 0.3pt, paint: black),
[0], [1], [1], [0], [0], [1], [0], [0], [类型标识 (TYP)], rowspanx(4)[数据单元标识符#linebreak()在 7.1 中定义],
[0], [0], [0], [0], [0], [0], [0], [1], [可变结构限定词 (VSQ)], (),
colspanx(8)[在 7.2.3 中定义], [传送原因 (COT)], (),
colspanx(8)[在 7.2.4 中定义], [应用服务数据单元公共地址], (),
colspanx(8)[在 7.2.5 中定义], [信息对象地址=0], rowspanx(2)[信息对象],
colspanx(8)[CP8], [QOI=召唤限定词(在 7.2.6.22 中定义)], ()
)
== 7.3.4.2 类型标识 101 : C_CI_NA_1
计数量召唤命令
单个信息对象(SQ = 0)
#tablex(
columns: 10,
align: center + horizon,
stroke: (thickness: 0.3pt, paint: black),
[0], [1], [1], [0], [0], [1], [0], [1], [类型标识(TYP)], rowspanx(4)[数据单元标识符#linebreak()在 7.1 中定义],
[0], [0], [0], [0], [0], [0], [0], [1], [可变结构限定词(VSQ)], (),
colspanx(8)[在 7.2.3 中定义], [传送原因(COT)], (),
colspanx(8)[在 7.2.4 中定义], [应用服务数据单元公共地址], (),
colspanx(8)[在 7.2.5 中定义], [信息对象地址=0], rowspanx(2)[信息对象],
colspanx(8)[CP8], [QCC=计数量召唤命令限定词(在 7.2.6.23 中定义)], (),
)
== 类型标识 102 : C_RD_NA_1
读命令
单个信息对象(SQ = 0)
#tablex(
columns: 10,
align: center + horizon,
stroke: (thickness: 0.3pt, paint: black),
[0], [1], [1], [0], [0], [1], [1], [0], [类型标识(TYP)], rowspanx(4)[数据单元标识符#linebreak()在 7.1 中定义],
[0], [0], [0], [0], [0], [0], [0], [1], [可变结构限定词(VSQ)], (),
colspanx(8)[在 7.2.3 中定义], [传送原因(COT)], (),
colspanx(8)[在 7.2.4 中定义], [应用服务数据单元公共地址], (),
colspanx(8)[在 7.2.5 中定义], [信息对象地址=0], [信息对象],
)
== 7.3.4.4 类型标识 103 : C_CS_NA_1
时钟同步命令
单个信息对象(SQ = 0)
#tablex(
columns: 10,
align: center + horizon,
stroke: (thickness: 0.3pt, paint: black),
[0], [1], [1], [0], [0], [1], [1], [1], [类型标识(TYP)], rowspanx(4)[数据单元标识符#linebreak()在 7.1 中定义],
[0], [0], [0], [0], [0], [0], [0], [1], [可变结构限定词(VSQ)], (),
colspanx(8)[在 7.2.3 中定义], [传送原因(COT)], (),
colspanx(8)[在 7.2.4 中定义], [应用服务数据单元公共地址], (),
colspanx(8)[在 7.2.5 中定义], [信息对象地址=0], rowspanx(2)[信息对象],
colspanx(8)[CP56Time2a 在 7.2.6.18 中定义], [七个八位位组二进制时间(从毫秒至年的日期和时钟时间)], ()
)
== 7.3.4.5 类型标识 104 : C_TS_NA_1
测试命令
单个信息对象(SQ = 0)
#tablex(
columns: 10,
align: center + horizon,
stroke: (thickness: 0.3pt, paint: black),
[0], [1], [1], [0], [1], [0], [0], [0], [类型标识(TYP)], rowspanx(4)[数据单元标识符#linebreak()在 7.1 中定义],
[0], [0], [0], [0], [0], [0], [0], [1], [可变结构限定词(VSQ)], (),
colspanx(8)[在 7.2.3 中定义], [传送原因(COT)], (),
colspanx(8)[在 7.2.4 中定义], [应用服务数据单元公共地址], (),
colspanx(8)[在 7.2.5 中定义], [信息对象地址=0], rowspanx(3)[信息对象],
[1], [0], [1], [0], [1], [0], [1], [0], rowspanx(2)[FBP=固定测试字(在 7.2.6.14 中定义)], (),
[0], [1], [0], [1], [0], [1], [0], [1], (), (),
)
== 7.3.4.6 类型标识 105 : C_RP_NA_1
复位进程命令
单个信息对象(SQ = 0)
#tablex(
columns: 10,
align: center + horizon,
stroke: (thickness: 0.3pt, paint: black),
[0], [1], [1], [0], [1], [0], [0], [1], [类型标识 (TYP)], rowspanx(4)[数据单元标识符#linebreak()在 7.1 中定义],
[0], [0], [0], [0], [0], [0], [0], [1], [可变结构限定词 (VSQ)], (),
colspanx(8)[在 7.2.3 中定义], [传送原因 (COT)], (),
colspanx(8)[在 7.2.4 中定义], [应用服务数据单元公共地址], (),
colspanx(8)[在 7.2.5 中定义], [信息对象地址=0], rowspanx(2)[信息对象],
colspanx(8)[UI8], [GRP=复位进程命令限定词(在 172.16.31.10 中定义)], ()
)
== 7.3.4.7 类型标识 106 : C_CD_NA_1
延时获得命令
单个信息对象(SQ = 0)
#tablex(
columns: 10,
align: center + horizon,
stroke: (thickness: 0.3pt, paint: black),
[0], [1], [1], [0], [1], [0], [1], [0], [类型标识(TYP)], rowspanx(4)[数据单元标识符#linebreak()在 7.1 中定义],
[0], [0], [0], [0], [0], [0], [0], [1], [可变结构限定词(VSQ)], (),
colspanx(8)[在 7.2.3 中定义], [传送原因(COT)], (),
colspanx(8)[在 7.2.4 中定义], [应用服务数据单元公共地址], (),
colspanx(8)[在 7.2.5 中定义], [信息对象地址=0], rowspanx(2)[信息对象],
colspanx(8)[CP16Time2a 在 7.2.6.20 中定义], [两个八位位组二进制时间(毫秒至秒)], ()
)
== 在控制方向参数的应用服务数据单元
== 7.3.5.1 类型标识 110 : P_ME_NA_1
测量值参数, 归一化值
单个信息对象(SQ = 0)
#tablex(
columns: 10,
align: center + horizon,
stroke: (thickness: 0.3pt, paint: black),
[0], [1], [1], [0], [1], [1], [1], [0], [类型标识(TYP)], rowspanx(4)[数据单元标识符#linebreak()在 7.1 中定义],
[0], [0], [0], [0], [0], [0], [0], [1], [可变结构限定词(VSQ)], (),
colspanx(8)[在 7.2.3 中定义], [传送原因(COT)], (),
colspanx(8)[在 7.2.4 中定义], [应用服务数据单元公共地址], (),
colspanx(8)[在 7.2.5 中定义], [信息对象地址], rowspanx(4)[信息对象],
colspanx(8)[值], rowspanx(2)[NVA=归一化值(在 7.2.6.6 中定义)], (),
[S], colspanx(7)[值], (), (),
colspanx(8)[CP8], [QPM=测量值参数限定词(在 7.2.6.24 中定义)], ()
)
== 7.3.5.2 类型标识 111 : P_ME_NB_1
测量值参数, 标度化值
单个信息对象(SQ = 0)
#tablex(
columns: 10,
align: center + horizon,
stroke: (thickness: 0.3pt, paint: black),
[0], [1], [1], [0], [1], [1], [1], [1], [类型标识(TYP)], rowspanx(4)[数据单元标识符#linebreak()在 7.1 中定义],
[0], [0], [0], [0], [0], [0], [0], [1], [可变结构限定词(VSQ)], (),
colspanx(8)[在 7.2.3 中定义], [传送原因(COT)], (),
colspanx(8)[在 7.2.4 中定义], [应用服务数据单元公共地址], (),
colspanx(8)[在 7.2.5 中定义], [信息对象地址=0], rowspanx(4)[信息对象],
colspanx(8)[值], rowspanx(2)[SVA=标度化值(在 7.2.6.7 中定义)], (),
[S], colspanx(7)[值], (), (),
colspanx(8)[CP8], [QPM=测量值参数限定词(在 7.2.6.24 中定义)], ()
)
== 7.3.5.3 类型标识 112 : P_ME_NC_1
测量值参数, 短浮点数
单个信息对象(SQ = 0)
#tablex(
columns: 10,
align: center + horizon,
stroke: (thickness: 0.3pt, paint: black),
[0], [1], [1], [1], [0], [0], [0], [0], [类型标识(TYP)], rowspanx(4)[数据单元标识符#linebreak()在 7.1 中定义],
[0], [0], [0], [0], [0], [0], [0], [1], [可变结构限定词(VSQ)], (),
colspanx(8)[在 7.2.3 中定义], [传送原因(COT)], (),
colspanx(8)[在 7.2.4 中定义], [应用服务数据单元公共地址], (),
colspanx(8)[在 7.2.5 中定义], [信息对象地址], rowspanx(6)[信息对象],
colspanx(8)[小数], rowspanx(4)[SVA=标度化值(在 7.2.6.7 中定义)], (),
colspanx(8)[小数], (), (),
[E], colspanx(7)[小数], (), (),
[S], colspanx(7)[指数], (), (),
colspanx(8)[UI8], [QPM=测量值参数限定词(在 7.2.6.24 中定义)], ()
)
== 7.3.5.4 类型标识 113 : P_AC_NA_1
参数激活
单个信息对象(SQ = 0)
#tablex(
columns: 10,
align: center + horizon,
stroke: (thickness: 0.3pt, paint: black),
[0], [1], [1], [1], [0], [0], [0], [1], [类型标识(TYP)], rowspanx(4)[数据单元标识符#linebreak()在 7.1 中定义],
[0], [0], [0], [0], [0], [0], [0], [1], [可变结构限定词(VSQ)], (),
colspanx(8)[在 7.2.3 中定义], [传送原因(COT)], (),
colspanx(8)[在 7.2.4 中定义], [应用服务数据单元公共地址], (),
colspanx(8)[在 7.2.5 中定义], [信息对象地址], rowspanx(2)[信息对象],
colspanx(8)[UI8], [QPA=参数激活限定词(在 7.2.6.25 中定义)], ()
)
|
|
https://github.com/JakMobius/courses | https://raw.githubusercontent.com/JakMobius/courses/main/mipt-os-basic-2024/sem07/main.typ | typst |
#import "@preview/polylux:0.3.1": *
#import "@preview/cetz:0.2.2"
#import "../theme/theme.typ": *
#import "../theme/asm.typ": *
#import "./utils.typ": *
#import "./bubbles.typ": *
#show: theme
#title-slide[
#align(horizon + center)[
= Процессы и потоки
АКОС, МФТИ
24 октября, 2024
]
]
#show: enable-handout
#let draw-core(x, y, size: 2, legs: 6, content: none) = {
let offset = 0.4
let leg-start = 0.2
let leg-end = 0.3
cetz.draw.content((x, y), {
box(
width: 1cm * size,
height: 1cm * size,
stroke: 5pt + black,
radius: 5pt,
content
)
})
cetz.draw.set-style(stroke: 4pt + luma(60), radius: 5pt);
for leg-x in range(legs) {
let x = x - size / 2 + offset + leg-x * (size - offset * 2) / (legs - 1)
let y = y - size / 2
cetz.draw.line((x, y - leg-start), (x, y - leg-end))
cetz.draw.line((x, y + leg-start + size), (x, y + size + leg-end))
}
for leg-y in range(legs) {
let x = x - size / 2
let y = y - size / 2 + offset + leg-y * (size - offset * 2) / (legs - 1)
cetz.draw.line((x - leg-start, y), (x - leg-end, y))
cetz.draw.line((x + size + leg-start, y), (x + size + leg-end, y))
}
}
#slide(background-image: none)[
#place(horizon + center)[
#cetz.canvas(length: 1cm, {
cetz.draw.content((0, 0), (28, -20), []);
let bubble-width = 8
let bubble-height = -6.5
draw-core(2.5, -10, legs: 10, size: 3, content: [
#set align(horizon + center)
= CPU
]);
cetz.draw.bezier((4, -7.5), (5.3, -6), (4, -6), fill: none, stroke: none, name: "bubbles")
draw-small-bubbles("bubbles", count: 3)
draw-bubble(7, -6, bubble-width, bubble-height);
cetz.draw.content((7, -3), (rel: (bubble-width, bubble-height)), padding: 0cm, [
#set align(center)
#set text(size: 30pt, weight: "bold")
Программа 1:
])
cetz.draw.content((18, -5), (rel: (bubble-width, bubble-height)), padding: 0cm, [
#set align(center)
#set text(size: 30pt, weight: "bold")
Программа 2:
])
cetz.draw.content((7, -6), (rel: (bubble-width, bubble-height)), padding: 0cm, [
#place(horizon + center)[
#set text(size: 30pt)
#lightasmtable(
```asm
mov rdi, 1
mov rdi, rax
mov rax, 0x4
syscall
...
```
)
]
]);
cetz.draw.content((18, -6), (rel: (bubble-width, bubble-height)), padding: 0cm, [
#place(horizon + center)[
#set text(size: 30pt)
#lightasmtable(
```asm
mov r10, 1
push r10
mov rdi, r10
call 0x10c90
```
)
]
]);
cetz.draw.line((7.3, -7), (7.3, -11), mark: (end: ">", width: 0.2cm, length: 0.3cm), stroke: (dash: "dashed", paint: gray, thickness: 4pt));
cetz.draw.bezier((22.5, -16.2), (22.5, -12.5), (24, -16.2), (22.5, -14.5), mark: (end: ">"), stroke: 5pt + black)
})
]
#place(bottom + center, dy: -1cm)[
= Как запустить вторую программу?
]
]
#slide(background-image: none)[
#place(center + top, dy: 1cm)[
#cetz.canvas(length: 1cm, {
cetz.draw.content((0, -4.5), (28, -4.5), []);
let bubble-width = 8
let bubble-height = -6
let left-fill = cell-color(blue).background-color
let right-fill = cell-color(red).background-color
let left-stroke-color = cell-color(blue).stroke-color
let right-stroke-color = cell-color(red).stroke-color
let left-stroke = 3pt + left-stroke-color
let right-stroke = 3pt + right-stroke-color
draw-core(3, -15.5, content: [
#set align(horizon + center)
= 1
]);
cetz.draw.bezier((1.1, -13.9), (2.3, -12), (1.1, -12), fill: none, stroke: none, name: "bubbles")
draw-small-bubbles("bubbles", count: 3, fill: left-fill, stroke: left-stroke)
draw-bubble(4, -6, bubble-width, bubble-height, fill: left-fill, stroke: left-stroke);
draw-core(16.7, -15.5, content: [
#set align(horizon + center)
= 2
]);
cetz.draw.bezier((14.7, -13.9), (15.9, -12), (14.7, -12), fill: none, stroke: none, name: "bubbles2")
draw-small-bubbles("bubbles2", count: 3, fill: right-fill, stroke: right-stroke)
draw-bubble(17.5, -6, bubble-width, bubble-height, fill: right-fill, stroke: right-stroke);
cetz.draw.content((4, -6), (rel: (bubble-width, bubble-height)), padding: 0cm, [
#place(horizon + center)[
#set text(size: 30pt)
#lightasmtable(
```asm
mov rdi, 1
mov rdi, rax
mov rax, 0x4
syscall
...
```
)
]
]);
cetz.draw.content((4.9, -14.6), (rel: (11, 3)), padding: 0cm, [
#set align(left)
#set text(size: 20pt)
#set block(spacing: 12pt)
== Первое ядро
Работает с программой 1
])
cetz.draw.content((18.7, -14.6), (rel: (11, 3)), padding: 0cm, [
#set align(left)
#set text(size: 20pt)
#set block(spacing: 12pt)
== Второе ядро
Работает с программой 2
])
cetz.draw.content((17.5, -6), (rel: (bubble-width, bubble-height)), padding: 0cm, [
#place(horizon + center)[
#set text(size: 30pt)
#lightasmtable(
```asm
mov r10, 1
push r10
mov rdi, r10
call 0x10c90
...
```
)
]
]);
cetz.draw.line((4.3, -7), (4.3, -11),
mark: (end: ">", width: 0.2cm, length: 0.3cm),
stroke: (
dash: "dashed",
paint: left-stroke-color.transparentize(50%),
thickness: 4pt
));
cetz.draw.line((17.8, -7), (17.8, -11),
mark: (end: ">", width: 0.2cm, length: 0.3cm),
stroke: (
dash: "dashed",
paint: right-stroke-color.transparentize(50%),
thickness: 4pt
));
})
]
#place(top + center)[
#set text(weight: "bold", size: 30pt)
Можно использовать несколько ядер!
]
#place(bottom + center, dy: -0.3cm)[
#set text(weight: "bold", size: 25pt)
#uncover((beginning: 2))[
Но ядер мало...
]
]
]
#slide(background-image: none)[
#align(center)[
= Можно ли выполнять две программы на одном ядре?
]
#place(horizon + center)[
#cetz.canvas(length: 1cm, {
cetz.draw.content((0, 0), (28, -15), []);
cetz.draw.content((12, -2.5), (rel: (4, 3)), [
#set align(center)
*Чередуя инструкции:*
])
let bubble-width = 8
let bubble-height = -6
let left-fill = cell-color(blue).background-color
let right-fill = cell-color(red).background-color
let left-stroke-color = cell-color(blue).stroke-color
let right-stroke-color = cell-color(red).stroke-color
let left-stroke = 3pt + left-stroke-color
let right-stroke = 3pt + right-stroke-color
let interp(a, b, k) = {
return a.enumerate().map(((i, x)) => (x * (1 - k) + b.at(i) * k))
}
cetz.draw.set-style(
stroke: (
dash: "dotted",
paint: luma(30),
thickness: 3pt
)
)
for i in range(0, 4) {
let base-y = -4.75
let line-height = 1.14
let y = base-y - i * line-height
let y2 = y + line-height
let a = (12, y)
let b = (16, y)
let b2 = (16, y2)
cetz.draw.circle(interp(a, b, 0.1), fill: left-fill, stroke: left-stroke, radius: 0.15)
cetz.draw.circle(interp(a, b, 0.9), fill: right-fill, stroke: right-stroke, radius: 0.15)
cetz.draw.line(interp(a, b, 0.2), interp(a, b, 0.8), mark: (end: ">"))
if i != 0 {
cetz.draw.line(interp(b2, a, 0.2), interp(b2, a, 0.8), mark: (end: ">"))
}
}
cetz.draw.set-style(mark: (:))
draw-core(14, -11.5, content: [
#set align(horizon + center)
= 1
]);
cetz.draw.bezier((12, -11.5), (9, -11.6), (10, -12.5), fill: none, stroke: none, name: "bubbles")
draw-small-bubbles("bubbles", count: 4, fill: left-fill, stroke: left-stroke)
draw-bubble(2, -4, bubble-width, bubble-height, fill: left-fill, stroke: left-stroke);
cetz.draw.bezier((16, -11.5), (18.9, -11.3), (18, -12.5), fill: none, stroke: none, name: "bubbles2")
draw-small-bubbles("bubbles2", count: 4, fill: right-fill, stroke: right-stroke)
draw-bubble(18, -4, bubble-width, bubble-height, fill: right-fill, stroke: right-stroke);
cetz.draw.content((2, -4), (rel: (bubble-width, bubble-height)), padding: 0cm, [
#place(horizon + center)[
#set text(size: 30pt)
#lightasmtable(
```asm
mov rdi, 1
mov rdi, rax
mov rax, 0x4
syscall
...
```
)
]
]);
cetz.draw.content((18, -4), (rel: (bubble-width, bubble-height)), padding: 0cm, [
#place(horizon + center)[
#set text(size: 30pt)
#lightasmtable(
```asm
mov r10, 1
push r10
mov rdi, r10
call 0x10c90
...
```
)
]
]);
})
]
#place(bottom + center, dy: -0.5cm)[
#set text(weight: "bold", size: 25pt)
Что пойдет не так?
]
]
#slide[
#place(horizon + center)[
#box[
#set text(size: 20pt)
#set align(left)
= Что пойдет не так?
#v(1em)
- Программы будут портить друг другу *регистры*;
#v(0.8em)
#uncover((beginning: 2))[
- ...И *память* (вспомним про адресные пространства).
]
#uncover((beginning: 3))[
= Как это починить?
]
#v(1em)
#uncover((beginning: 4))[
- Возложить на ядро ответственность за *разделение ресурсов*.
]
]
]
]
#slide(background-image: none)[
#place(horizon + center, dy: -0.5cm)[
#cetz.canvas(length: 1cm, {
cetz.draw.content((0, 0), (30, -15), []);
let x0 = 0
let x1 = 20
let jitter = 0.1
let jagged-border(x1, x2, y, peak-freq: 4) = {
let points = ()
let peaks = calc.floor((x2 - x1) * peak-freq)
for i in range(0, peaks) {
let x = x1 + i * (x2 - x1) / peaks
let y = y + if calc.rem(i, 2) == 0 { jitter } else { -jitter }
points.push((x, y))
}
if calc.rem(peaks, 2) == 0 {
points.push((x2, y + jitter))
} else {
points.push((x2, y - jitter))
}
points
}
let draw-background(y1, y2, color, content) = {
y1 += jitter
y2 -= jitter
let bg = cell-color(color).background-color
let stroke = cell-color(color).stroke-color
cetz.draw.rect((x0, y1), (x1, y2), fill: bg, stroke: none)
cetz.draw.content((x0, y1), (x1, y2), [
#set text(fill: stroke)
#content
])
}
let draw-ripped-section(y1, y2, content) = {
let path1 = jagged-border(x0, x1, y1)
// let path2 = jagged-border(0, 30, y2).rev()
let path2 = ((x1, y2), (x0, y2))
let path = path1 + path2
let bg = cell-color(black).background-color
let stroke = cell-color(black).stroke-color
cetz.draw.line(..path1, stroke: 5pt + stroke)
cetz.draw.line(..path2, stroke: (thickness: 5pt, paint: stroke, dash: "solid"))
cetz.draw.line(..path, close: true, fill: bg, stroke: none)
cetz.draw.content((x0, y1), (x1, y2), content)
}
let row(left-content, right-content) = {
grid(
columns: (40%, 60%),
rows: 100%,
align: horizon + left,
inset: (x, y) => {
if x == 0 { (x: 20pt, y: 20pt) }
else { (:) }
},
stroke: none,
[
#set text(size: 25pt, weight: "semibold")
#left-content
],
right-content)
}
let userspace-height = 4
let kernelspace-height = 2.5
let y = 0
let kernel-row = row([
Код ядра ОС
], [
#box(inset: (x: 15pt))[
#set text(size: 20pt)
_Переключение контекста_
]
])
let userspace-row(header, asm) = {
row(header, [
#set text(size: 30pt)
#lightasmtable(asm)
])
}
let rows = (
("userspace", blue, [
#userspace-row([Контекст 1],
```asm
mov rdi, 1
mov rsi, rax
```
)
]),
("kernel",),
("userspace", red, [
#userspace-row([Контекст 2],
```asm
mov r10, 1
push r10
```
)
]),
("kernel",),
("userspace", blue, [
#userspace-row([Контекст 1],
```asm
mov rax, 0x4
syscall
```
)
])
)
let y = 0;
for row in rows {
if row.at(0) == "userspace" {
draw-background(y, y - userspace-height, row.at(1), row.at(2))
y -= userspace-height
} else {
y -= kernelspace-height
}
}
y = 0
for row in rows {
if row.at(0) == "kernel" {
draw-ripped-section(y, y - kernelspace-height, kernel-row)
y -= kernelspace-height
} else {
y -= userspace-height
}
}
let bubbles = generate-bubble-wall(x1 - 1.5, 0, x1 - 1.5, -20, 17)
for (x, y, r) in bubbles {
// cetz.draw.circle((x, y), radius: r, fill: white, stroke: 3pt + black)
}
let points = bubbles-to-path(bubbles)
let gradient = gradient.radial(white, rgb(91%, 91.3%, 91.35%))
cetz.draw.merge-path(close: true, fill: gradient, stroke: 3pt + black, {
cetz.draw.hobby(..points, stroke: 3pt + black)
cetz.draw.line((), (x1, -22), (30, -22), (30, 5))
})
draw-core(26, -15, size: 3, legs: 10, content: [
#set align(horizon + center)
#image("img/struggling-face.png", width: 80%, height: 80%)
])
cetz.draw.bezier((23.5, -14.5), (20.2, -14), (20.2, -14.5), fill: none, stroke: none, name: "bubbles")
draw-small-bubbles("bubbles", count: 4, fill: white)
let y-int = -3
let y-usr = -5.5
cetz.draw.content((22, y-int), (rel: (6, 2)), name: "interrupts", [
#set align(horizon + left)
#set block(spacing: 10pt)
#set text(fill: luma(50), size: 20pt, weight: "semibold")
#box(inset: 10pt)[
Прерывания по~таймеру
#v(0.1em)
#text(size: 14pt)[
_60 - 1000 раз / сек._
]
]
])
cetz.draw.content((23, y-usr), (rel: (6, 2)), name: "userspace", [
#set align(horizon + left)
#set text(fill: luma(50), size: 20pt, weight: "semibold")
#box(inset: 10pt)[
Переходы в Userspace
]
])
let draw-bezier(x0, y0, x1, y1, xd: 0) = {
cetz.draw.merge-path({
cetz.draw.bezier((x1, y1), (x0, y0), (x0, y1), (x1, y0))
if xd != 0 {
cetz.draw.line((), (x0 + xd, y0))
}
}, stroke: (dash: "dashed", paint: luma(100), thickness: 3pt))
}
draw-bezier(20, -4, 22, y-int - 1)
draw-bezier(20, -10.5, 22, y-int - 1)
draw-bezier(21, -6.5, 23, y-usr - 1, xd: -1)
draw-bezier(21, -13, 23, y-usr - 1, xd: -1)
})
]
]
#slide(place-location: horizon + center)[
#box[
#text(size: 25pt)[
= Как переключить контекст
]
#v(2em)
#set align(left)
*1.* *Сохранить* в память контекст текущей программы;
*2.* *Восстановить* из памяти контекст новой программы;
*3.* Перейти в Userspace и *продолжить исполнение* новой программы.
#align(center)[
#v(0.5em)
#line(length: 80%)
#v(0.5em)
]
- Происходит по прерыванию таймера;
- *Позволяет одновременно запустить много программ на одном ядре*.
]
]
#slide[
#place(horizon + center, dy: -0.5cm)[
== Переходим к правильным терминам:
#v(0.5em)
#box(
stroke: 3pt + cell-color(blue).stroke-color,
fill: cell-color(blue).background-color,
radius: 20pt,
inset: (x: 40pt, top: 18pt, bottom: 40pt)
)[
#set text(size: 30pt, weight: "bold")
Программа $arrow.r$ #colbox(
inset: 15pt,
color: rgb(60, 60, 60),
baseline: 15pt,
[
Процесс
])
#set align(left)
#set text(size: 20pt, weight: "regular")
- Имеет свой *номер* (PID)
- Имеет свой *контекст выполнения*
- Имеет своё *адресное пространство*
- Имеет свой *набор дескрипторов*
- Знает своего *родителя* и *пользователя*
- _И еще много чего..._
]
]
]
#slide(background-image: none)[
= Создаём процессы, как это делали наши отцы
== #codebox(lang: "c", "fork()")
- *Дублирует* текущий процесс, включая указатель на текущую инструкцию;
- *Возвращается дважды*:
- В созданном процессе возвращает #codebox(lang: "c", "0") ;
- В родительском процессе возвращает номер (PID) созданного процесса.
== #codebox(lang: "c", "exec(...)")
- *Заменяет* текущий процесс на новый процесс по командной строке;
- Имеет много вариаций: #codebox(lang: "c", "execl(...)"), #codebox(lang: "c", "execv(...)"), #codebox(lang: "c", "execve(...)") и т.д;
- *Наследует настройки* родительского процесса: открытые дескрипторы, переменные окружения, рабочую директорию, маски сигналов и т.д.
]
#slide(background-image: none, place-location: horizon + center)[
#text(weight: "bold", size: 25pt)[
#set align(center)
== #codebox(lang: "c", "fork()") + #codebox(lang: "c", "exec()")
#box(width: 20cm, stroke: 3pt + black, inset: 20pt, radius: 20pt, fill: white)[
#code(numbers: true,
```c
if (fork() == 0) {
// Здесь можно закрыть всё лишнее
// И заместить себя другим процессом
execl("/bin/bash", NULL);
}
// Здесь полезная работа родителя
wait(NULL); // Ждём завершения потомка
```
)
]
...или как написать свой #bash("bash") в 9 строк.
]
]
#slide[
#set text(weight: "bold", size: 25pt)
#place(horizon + center, dy: -5cm)[
= А что, если...
]
#place(horizon + center)[
#box(width: 13cm, stroke: 3pt + black, inset: (x: 20pt, y: 40pt), radius: 20pt, fill: white)[
#code(numbers: true,
```c
while (true) {
fork();
}
```
)
]
]
#place(horizon + center, dy: 4.5cm)[
=== ...и отбежать на безопасное расстояние?
]
]
#slide(background-image: none)[
= Создаём процессы модно
== #codebox(lang: "c", "posix_spawn(pid_t* pid, char* file, /* whole lot of arguments */)")
#v(0.5em)
- Умно-хитро *создаёт новый процесс* по командной строке и исполняемому файлу.
- Даёт *широкий набор настроек* для создаваемого процесса, например:
#table(
columns: 2,
inset: (left: 20pt, right: 20pt, y: 0pt),
stroke: (x, y) => {
if x == 0 {
(right: 3pt + gray)
} else {
none
}
},
row-gutter: 10pt,
align: horizon,
codebox(lang: "c", "posix_spawnattr_setsigmask(...)"), [Настройка маски сигналов;],
codebox(lang: "c", "posix_spawnattr_getpgroup(...)"), [Настройка группы процессов;],
codebox(lang: "c", "posix_spawnattr_setschedparam(...)"), [Настройка параметров планирования;],
codebox(lang: "c", "posix_spawn_file_actions_xxxxxx(...)"), [Открытие и закрытие дескрипторов.],
)
- *Быстрее, чем #codebox(lang: "c", "fork()") + #codebox(lang: "c", "exec()")* .
]
#slide(background-image: none)[
= Дожидаемся процессов
== #codebox(lang: "c", "waitpid(pid_t pid, int* status, int options)")
*Ждёт завершения процесса* и возвращает статус завершения.
#table(columns: 2,
align: horizon,
inset: (x, y) => {
if x == 0 { (left: 10pt, right: 20pt)}
else {(left: 20pt, right: 20pt, y: 0pt)}
},
stroke: (x, y) => {
if x == 0 and y != 2 {
(right: 3pt + gray)
} else {
none
}
},
row-gutter: (8pt,) * 2 + (4pt,) * 3,
codebox(lang: "c", "pid_t pid"), [*Процесс*, которого нужно дождаться. #codebox(lang: "c", "-1") = любой дочерний;],
codebox(lang: "c", "int* status"), [Куда вернуть *статус завершения* процесса. Может быть #codebox(lang: "c", "NULL");],
[#codebox(lang: "c", "int options") :], [],
[#raw("|= ")#codebox(lang: "c", "WNOHANG")], [*Не ждать* дочерний процесс, если он ещё работает;],
[#raw("|= ")#codebox(lang: "c", "WUNTRACED")], [Сработать на *остановку* процесса (#codebox("SIGSTOP")).],
[#raw("|= ")#codebox(lang: "c", "WCONTINUED")], [Сработать на *возобновление* процесса (#codebox("SIGCONT")).]
)
#line(length: 100%)
#set block(below: 10pt, above: 15pt)
#codebox(lang: "c", "wait(status)") $equiv$ #codebox(lang: "c", "waitpid(-1, status, 0)") . И то, и то под капотом -- #codebox(lang: "c", "wait4(...)").
#colbox(color: red)[⚠️] : *Ждать нужно каждого дочернего процесса*, иначе они станут зомби.
]
#slide(place-location: horizon + center, background-image: none)[
#image("img/zombie.jpg")
]
#slide[
= Статусы #codebox(lang: "c", "waitpid(...)")
#colbox(color: gray)[⚠️] : Статус, который передаёт #codebox(lang: "c", "waitpid(...)") -- это *не код завершения процесса.*
*Это битовая маска*, которую можно декодировать библиотечными функциями:
#table(
columns: 2,
align: horizon,
inset: (x, y) => {
if x == 0 {
(left: 20pt, right: 20pt)
} else {
(left: 20pt, right: 20pt, y: 0pt)
}
},
stroke: (x, y) => {
if x == 0 {
(right: 3pt + gray)
} else {
none
}
},
row-gutter: 10pt,
codebox(lang: "c", "WIFEXITED(status)"), [Процесс завершился *нормально*;],
codebox(lang: "c", "WIFSTOPPED(status)"), [Процесс *приостановлен*;],
codebox(lang: "c", "WIFCONTINUED(status)"), [Процесс *возобновлен*;],
codebox(lang: "c", "WIFSIGNALED(status)"), [Процесс завершился *сигналом*;],
codebox(lang: "c", "WEXITSTATUS(status)"), [Какой *код завершения* вернул процесс;],
codebox(lang: "c", "WSTOPSIG(status)"), [Какой *сигнал* приостановил процесс;],
codebox(lang: "c", "WTERMSIG(status)"), [Какой *сигнал* завершил процесс;],
)
]
#focus-slide[
#text(size: 30pt)[
*Как использовать несколько ядер в одном процессе?*
]
]
#slide[
#place(horizon + center, dy: -0.5cm)[
#box(
stroke: 3pt + cell-color(yellow).stroke-color,
fill: cell-color(yellow).background-color,
radius: 20pt,
inset: (x: 40pt, top: 18pt, bottom: 40pt)
)[
#v(1em)
#set text(size: 40pt, weight: "bold")
Поток
#set align(left)
#set text(size: 20pt, weight: "regular")
- Имеет свой *номер* (TID)
- Имеет свой *контекст выполнения*
- Имеет свой *стек*
#line(length: 50%)
- Является *частью процесса*
- Почти всё *делит с другими потоками*
- *Общее адресное пространство*
- *Общий набор дескрипторов*
]
]
]
#slide(background-image: none)[
= Зачем нужны потоки?
#table(
columns: (40%, 60%),
align: left + horizon,
stroke: (x, y) => {
if x == 1 {
return (left: 3pt + gray)
}
},
inset: (x, y) => {
if x == 1 {
return (left: 20pt, top: 20pt)
}
return (top: 20pt)
},
[
#align(center)[
#cetz.canvas(length: 1cm, {
cetz.draw.content((0, 0), (rel: (8, 8)), [
#image("img/render.png")
])
cetz.draw.content((0, 0), (rel: (8, 8)), [
#grid(
columns: (50%, 50%),
rows: (50%, 50%),
stroke: 5pt + black.transparentize(50%),
align: horizon + center,
..range(4).map(i => [
#set text(size: 50pt, fill: black.transparentize(50%), weight: "bold")
#(i + 1)
])
)
])
})
]
], [
*Потоки позволяют осуществлять параллельные вычисления внутри процесса.*
- Например, для софтверного рендеринга:
- Разделить картинку на несколько частей;
- Каждую часть рендерить в своём потоке.
#colbox(color: red)[⚠️] : *Потоки и процессы - не одно и то же!*
]
)
= #codebox(lang: "c", "pthread")
- *Ваш инструмент* для создания потоков и контроля над ними.
- Подключается через #codebox(lang: "c", "#include <pthread.h>") и флаг #codebox("-pthread") .
]
#slide(background-image: none)[
== #codebox(lang: "c", "pthread_create(pthread_t*, pthread_attr_t*, f* function, void* arg);")
*Конструктор структуры #codebox(lang: "c", "pthread_t")*
#table(columns: 2,
align: horizon,
inset: (x, y) => {
if x == 0 { (left: 10pt, right: 20pt)}
else {(left: 20pt, right: 20pt, y: 0pt)}
},
stroke: (x, y) => {
if x == 0 {
(right: 3pt + gray)
} else {
none
}
},
row-gutter: 8pt,
codebox(lang: "c", "pthread_t thread"), [*Структура*, которую нужно инициализировать],
codebox(lang: "c", "const pthread_attr_t* attr"), [*Атрибуты* потока],
codebox(lang: "c", "(void*)(*function)(void*)"), [*Entrypoint* потока],
[#codebox(lang: "c", "void* arg") :], [*Аргумент* для entrypoint],
)
#line(length: 100%)
#colbox(color: gray)[⚠️] : *Деструктора у #codebox(lang: "c", "pthread_t") нет,* только у атрибутов.
- Поток уничтожится сам, когда выполнятся определённые условия.
]
#slide(background-image: none)[
= Атрибуты потока -- #codebox(lang: "c", "pthread_attr_t")
#table(columns: 2,
align: horizon,
inset: (x, y) => {
if x == 0 { (left: 10pt, right: 20pt)}
else {(left: 20pt, right: 20pt, y: 0pt)}
},
stroke: (x, y) => {
if x == 0 and y != 6 {
(right: 3pt + gray)
} else {
none
}
},
row-gutter: 8pt,
codebox(lang: "c", "pthread_attr_init(...)"), [*Конструктор*;],
codebox(lang: "c", "pthread_attr_destroy(...)"), [*Деструктор* (да, у атрибутов он есть);],
codebox(lang: "c", "pthread_attr_setstacksize(...)"), [Запросить другой *размер стека*;],
codebox(lang: "c", "pthread_attr_setguardsize(...)"), [Запросить другой *размер guard-секции*;],
codebox(lang: "c", "pthread_attr_setstack(...)"), [Установить *собственный стек*;],
codebox(lang: "c", "pthread_attr_setaffinity_np(...)"), [Настроить набор процессорных ядер;],
box(inset: (y: 10pt))[_И еще много чего..._], []
)
#line(length: 100%)
Если вас устраивают *атрибуты по умолчанию*, можно передать #codebox(lang: "c", "NULL")
Атрибуты можно освободить сразу после создания потока, либо переиспользовать.
]
#slide(background-image: none, place-location: horizon)[
#table(
columns: (50%, 50%),
align: top + center,
inset: (y: 20pt, x: 10pt),
stroke: none,
[
#box(
inset: 20pt,
radius: 20pt,
height: 8cm,
stroke: 3pt + cell-color(blue).stroke-color,
fill: cell-color(blue).background-color
)[
== Неявное завершение работы
#line(length: 100%, stroke: 3pt + cell-color(blue).stroke-color.transparentize(80%))
#set align(left)
- *Поток завершил свою работу*, вернувшись из своей функции.
]
],
[
#box(
inset: 20pt,
radius: 20pt,
stroke: 3pt + cell-color(red).stroke-color,
fill: cell-color(red).background-color,
height: 8cm,
)[
== Явное завершение работы
#line(length: 100%, stroke: 3pt + cell-color(red).stroke-color.transparentize(80%))
#set align(left)
#set block(spacing: 10pt)
- *Поток явно завершил работу*:
#h(1em) #codebox(lang: "c", "pthread_exit(...)")
#v(0.5cm)
- *Другой поток отменил его*:
#h(1em) #codebox(lang: "c", "pthread_cancel(...)")
]
]
)
*Поток освобождается*, когда он завершил свою работу и:
- Либо его *дождался* другой поток через #codebox(lang: "c", "pthread_join(...)");
- Либо его *пометили как отсоединённый* через #codebox(lang: "c", "pthread_detach(...)");
]
#let ub = (content) => {
place(bottom)[
#box(
inset: (bottom: 20pt, top: 15pt),
outset: (x: 40pt, bottom: 20pt),
width: 100%,
fill: red.desaturate(80%),
stroke: (top: 3pt + red.darken(50%))
)[
#content
]
]
}
#slide(background-image: none)[
= #codebox(lang: "c", "pthread_join(pthread_t tid, void **status)")
*Ждет завершения потока* и возвращает статус завершения.
#table(columns: 2,
align: horizon,
inset: (x, y) => {
if x == 0 { (left: 10pt, right: 20pt)}
else {(left: 20pt, right: 20pt, y: 0pt)}
},
stroke: (x, y) => {
if x == 0 and y != 2 {
(right: 3pt + gray)
} else {
none
}
},
row-gutter: (8pt,) * 2 + (4pt,) * 3,
codebox(lang: "c", "pthread_t tid"), [*Поток*, которого нужно дождаться.],
codebox(lang: "c", "void** status"), [Куда вернуть *статус завершения* процесса. Может быть #codebox(lang: "c", "NULL");],
)
#line(length: 100%)
- *#codebox(lang: "c", "pthread_join(...)") - аналог #codebox(lang: "c", "waitpid(...)") для потоков.*
- *Если поток был отменён*, то вместо кода возврата вернётся #codebox("PTHREAD_CANCELED").
- Пока вы не вызовете #codebox(lang: "c", "pthread_join(...)"), поток *не сможет освободиться*.
#ub[
== #colbox(color: red)[⚠️] Осторожно, UB!
- *После #codebox(lang: "c", "pthread_join(...)") поток уже освобождён.*
- Работа с ним - *UB*
]
]
#slide(background-image: none)[
= #codebox(lang: "c", "pthread_detach(pthread_t tid)")
*Помечает поток как отсоединённый*. Ничего не ждёт.
Отсоединенный поток освобождается из памяти *сразу по завершении работы*.
#line(length: 100%)
Если проще - #codebox(lang: "c", "pthread_detach(...)") $equiv$ #codebox(lang: "c", "pthread_join(...)") отложенного действия.
Этим можно пользоваться, когда код возврата не нужен.
#ub[
== #colbox(color: red)[⚠️] Осторожно, здесь тоже UB!
- *После #codebox(lang: "c", "pthread_detach(...)") поток может освободиться в любой момент.*
- Работа с ним - *UB*
]
]
#let ub-header = (content) => {
place(top, float: true)[
#box(
inset: (bottom: 20pt, top: 0pt),
outset: (x: 40pt, top: 30pt),
width: 100%,
fill: red.desaturate(80%),
stroke: (bottom: 3pt + red.darken(50%))
)[
#content
]
]
}
#slide(background-image: none)[
#ub-header[
= #colbox(color: red)[⚠️] Кругом UB!
]
*Не все стандартные функции любят, когда их используют многопоточно.* Например:
#align(center)[
#box(inset: 0pt)[
#table(columns: 4,
stroke: (x, y) => {
if x != 0 {
(left: 3pt + gray)
} else {
(:)
}
},
row-gutter: 5pt,
inset: (x: 15pt, y: 3pt),
align: center + horizon,
[#codebox(lang: "c", "crypt()")],
[#codebox(lang: "c", "ctime()")],
[#codebox(lang: "c", "encrypt()")],
[#codebox(lang: "c", "dirname()")],
[#codebox(lang: "c", "localtime()")],
[#codebox(lang: "c", "rand()")],
[#codebox(lang: "c", "strerror()")],
[#codebox(lang: "c", "getdate()")],
)
]
]
- *Функции могут иметь разную толерантность к многопоточности*. Например:
- Быть безопасными, *но не на первом вызове*;
- Быть безопасными, *но не на одинаковых объектах*;
- Быть безопасными, *но только если окружение не меняется*;
- И так далее.
*Об этом подробно сказано в мануалах (#link("https://man7.org/linux/man-pages/man7/attributes.7.html")[man 7 attributes], #link("https://man7.org/linux/man-pages/man7/pthreads.7.html")[man 7 pthreads])*
#place(bottom + center, dy: -0.2cm)[
_Многопоточное программирование кишит UB, но об этом в следующий раз._
]
]
#title-slide[
#place(horizon + center)[
= Спасибо за внимание!
]
#place(
bottom + center,
)[
// #qr-code("https://github.com/JakMobius/courses/tree/main/mipt-os-basic-2024", width: 5cm)
#box(
baseline: 0.2em + 4pt, inset: (x: 15pt, y: 15pt), radius: 5pt, stroke: 3pt + rgb(185, 186, 187), fill: rgb(240, 240, 240),
)[
🔗 #link(
"https://github.com/JakMobius/courses/tree/main/mipt-os-basic-2024",
)[*github.com/JakMobius/courses/tree/main/mipt-os-basic-2024*]
]
]
] |
|
https://github.com/thanhdxuan/dacn-report | https://raw.githubusercontent.com/thanhdxuan/dacn-report/master/report-week-5/contents/03-datacollection.typ | typst | = Tìm kiếm & Thu thập dữ liệu (Data collection)
== Tập dữ liệu 1 @H_2022
*Mô tả:* Tập dữ liệu được thu thập được các ngân hàng thu thập từ các khoản vay trước đây, nhằm mục đích xây dựng các mô hình dự đoán dựa trên các kỹ thuật khai phá dữ liệu, học máy. Để từ đó, phân loại các người đi vay xem họ có khả năng vỡ nợ hay không.\
*Thời gian thu thập dữ liệu:* 2019 \
*Độ lớn:* hơn 140.000 dòng, với 34 thuộc tính.\
*Nguồn:* Tập dữ liệu được giới thiệu bởi Kaggle - Một cộng đồng chia sẻ các nguồn dữ liệu đáng tin cậy, được nhiều bài báo về chủ đề dữ liệu, học máy sử dụng.\
#let attributes = (
ID: "Mã số khoản vay.",
year: "Năm dữ liệu được ghi nhận.",
loan_limit: "Giới hạn khoản vay.",
Gender: "Giới tính.",
approv_in_adv: "Đã được phê duyệt trước.",
loan_type: "Loại khoản vay.",
loan_purpose: "Mục đích vay.",
Credit_Worthiness: "Uy tín tín dụng.",
open_credit: "Tín dụng mở. (Tín dụng xoay vòng)",
business_or_commercial: "Kinh doanh hoặc thương mại",
loan_amount: "Khoản vay.",
rate_of_interest: "Lãi suất.",
Interest_rate_spread: "Chênh lệch lãi suất (lãi suất cho vay - lãi suất tiền gửi).",
Upfront_charges: "Lệ phí mà người đi vay phải trả trước khi khoản vay được chấp nhận.",
term: "Kì hạn vay",
Neg_ammortization: "Thoả thuận trả góp hàng tháng",
interest_only: "Khoản vay theo lịch trình (chỉ cần trả lãi)",
lump_sum_payment: "Khoản vay được chia thành nhiều đợt trả hay không",
property_value: "Giá trị tài sản.",
construction_type: "",
occupancy_type: "",
Secured_by: "",
total_units: "",
income: "Thu nhập của người vay.",
credit_type: "Loại tổ chức đánh giá điểm tín dụng",
Credit_Score: " Điểm tín dụng, được tính dựa trên lịch sử trả nợ và hồ sơ tín dụng của người vay.",
co-applicant_credit_type: "Thang điểm đánh giá tín dụng của người đi vay cùng (nếu có).",
age: "Tuổi",
submission_of_application: "",
LTV: "loan-to-value là tỉ lệ khoản tiền thế chấp trên giá trị thẩm định của tài sản",
Region: "Khu vực",
Security_Type: "",
Status: "Kết quả đánh giá.",
dtir1: ""
)
*Các thuộc tính:*\
#for (name, description) in attributes {
[
- _#name:_ #description
]
}
== Tập dữ liệu 2 @ItsSuru_2021
*Mô tả:* Tập dữ liệu từ LendingClub.com, tập dữ liệu được thu thập từ các khoản đầu tư trong quá khứ để phân tích, đánh giá, giúp cho các nhà đầu tư có thể có xác suất đầu tư vào các đối tượng có khả năng hoàn vốn cao mình.
*Thời gian thu thập dữ liệu:* 2007 - 2010 \
*Độ lớn:* hơn 9.578 dòng, với 14 thuộc tính.\
*Nguồn:* Tập dữ liệu được thu thập từ LendingClub.com - Nền tảng giúp kết nối những người cần vay tiền với những người có tiền để cho vay (nhà đầu tư). Đây là nền tảng cung cấp các dịch vụ tài chính có trụ sở tại Mỹ, có uy tín cao trong ngành tài chính, đầu tư.
#let attributes_2 = (
"credit.policy": "1 nếu người dùng đáp ứng các tiêu chí đánh giá của LendingClub.com, và ngược lại là 0.",
"purpose": "Mục đích của khoản vay (nhận các giá trị: credit_card, debt_consolidation, educational, major_purchase, small_business, and all_other)",
"int.rate": "Lãi suất khoản vay, người đi vay được LendingClub.com đánh giá có mức rủi ro cao sẽ có mức lãi suất cao hơn",
"installment": "Số tiền trả góp hàng tháng nếu khoản vay được chấp nhận.",
"log.annual.inc": "Nhật ký về thu nhập hàng năm tự sao kê của người đi vay.",
"dti": "debt-to-income: Tỷ lệ nợ trên thu nhập của người đi vay.",
"fico": "Điểm tín dụng FICO của người đi vay.",
"days.with.cr.line": "Số ngày người đi vay tín dụng.",
"revol.bal": "Số dư xoay vòng của người đi vay (số tiền chưa thanh toán ở mỗi kỳ thanh toán tín dụng).",
"revol.util": "Tỉ lệ sử dụng hạn mức tín dụng xoay vòng của người cho vay.",
"inq.last.6mths": "Số lượng yêu cầu vay của người đi vay trong 6 tháng vừa qua.",
"delinq.2yrs": "Số lần người đi vay quá hạn hơn 30 ngày trong vòng 2 năm qua.",
"pub.rec": "Số lượng hồ sơ công khai của người vay."
)
*Các thuộc tính:*\
#for (name, description) in attributes_2 {
[
- _#name:_ #description
]
}
|
|
https://github.com/linxuanm/math-notes | https://raw.githubusercontent.com/linxuanm/math-notes/master/topology/1-topology.typ | typst | #import "../setup.typ": *
#show: lecenv
#show: thmrules
= Basic Definitions
#definition[
A #bold[topology] $tau$ on a set $X$ is a set satisfying the following axioms:
+ $nothing in tau$ and $X in tau$.
+ $tau$ is closed under finite intersections.
+ $tau$ is closed under arbitrary unions.
]
Members of $tau$ are called #bold[open sets].
#example[
The set of open intervals $(a, b)$ on #bR forms a topology on #bR.
+ The empty set and $bb(R)$ are both open.
+ Open intervals are closed under finite intersections.
+ Open intervals are closed under arbitrary unions.
]
The set of closed intervals $[a, b]$ on $bR$ #bold[does not] form a topology on #bR. Consider the union:
$ union.big_(i in bb(N)) [-2 + 1/i, 2 - 1/i] $
This forms an open interval $[-2, 2]$, showing that the set of closed interval is not closed under arbitrary unions.
#definition[
The #bold[discrete topology] $tau$ on a set $X$ is the powerset of $X$, i.e., $tau = cal(X)$.
+ $nothing$ and $X$ are both subsets of $X$, thereby $nothing in tau$ and $X in tau$.
+ If $A, B in cal(P)(X)$, then $i in A sect B => i in A subset.eq X$, so $A sect B subset.eq X => A sect B in tau$.
+ Let $S$ be a (possibly infinite) set of subsets of $X$ so that $S subset.eq tau$. No element of $S$ can contain an element not in $X$, so $union.big S subset.eq X => union.big S in tau$.
]
#definition[
The #bold[trivial topology] on a set $X$ is the set $tau = {nothing, X}$.
+ $nothing in tau$ and $X in tau$.
+ Let $S subset.eq tau$:
- If $nothing in S$, then $sect.big S = nothing$.
- If $nothing in.not S$, then $sect.big S = X$.
+ Let $S subset.eq tau$:
- If $X in S$, then $union.big S = X$.
- If $X in.not S$, then $union.big S = nothing$.
]
#definition[
Let $(M, d)$ be a metric space. Its #bold[metric topology] is the collection of open sets (in the metric space sense) in $M$, i.e., for every element $i$ in an open set $S$, there exists $epsilon > 0$ such that all elements $j$ satisfying $d(i, j) < epsilon$ are also in $S$.
]
#definition[
Given a topology $(X, tau)$. A subset $S subset.eq X$ is a #bold[closed set] if its complement $S backslash X$ is open.
]
|
|
https://github.com/augustebaum/epfl-thesis-typst | https://raw.githubusercontent.com/augustebaum/epfl-thesis-typst/main/example/head/cover-page.typ | typst | MIT License | #page(
numbering: none, margin: (y: 6cm), {
set text(font: "Latin Modern Sans")
align(
center, [
#let v-skip = v(1em, weak: true)
#let v-space = v(2em, weak: true)
#text(size: 18pt)[
FIRST LINE OF TITLE\
SECOND LINE OF TITLE
]
#v-space
#text(fill: gray)[
THIS IS A TEMPORARY TITLE PAGE
It will be replaced for the final print by a version\
provided by the service académique.
]
#v-space
#v(1fr)
#grid(
columns: (1fr, 60%), align(horizon, image("../images/Logo_EPFL.svg", width: 75%)), align(left)[
Thèse n. 1234 2011\
présentée le 12 Mars 2011\
à la Faculté des Sciences de Base\
laboratoire SuperScience\
programme doctoral en SuperScience\
École Polytechnique Fédérale de Lausanne\
#v-skip
pour l’obtention du grade de Docteur ès Sciences\
par\
#h(2cm) Your Name\
#v-space
acceptée sur proposition du jury:\
#v-skip
Prof Name Surname, président du jury\
Prof Name Surname, directeur de thèse\
Prof Name Surname, rapporteur\
Prof Name Surname, rapporteur\
Prof Name Surname, rapporteur
#v-space
Lausanne, EPFL, 2011
],
)
],
)
},
)
|
https://github.com/longlin10086/HITSZ-PhTyp | https://raw.githubusercontent.com/longlin10086/HITSZ-PhTyp/main/utils/head_element.typ | typst | #import "../themes/theme.typ" : *
#import "image.typ" : teacher_signature
#let underline_element(
name,
body,
size
) = {
set text(font: 字体.黑体, size: 字号.五号,lang: "zh", region: "cn")
strong(name)
h(size)
underline(offset: 2pt, extent: size, evade: false, body)
}
#let head_elements_line(
class,
id,
name,
signature,
date,
preview_score,
all_scores
) = {
set align(left)
grid(
columns: (1.2fr, 1.2fr, 1.2fr, 1fr),
underline_element("班级", class, 15pt),
underline_element("学号", id, 15pt),
underline_element("姓名", name, 20pt),
teacher_signature("教师签名", signature),
)
grid(
columns: (1fr, 1fr, 1fr),
underline_element("实验日期", date, 30pt),
underline_element("预习成绩", preview_score, 30pt),
underline_element("总成绩", all_scores, 30pt),
)
}
|
|
https://github.com/typst/packages | https://raw.githubusercontent.com/typst/packages/main/packages/preview/cineca/0.1.0/README.md | markdown | Apache License 2.0 | # CINECA: A Typst Package to Create Calendars
CINECA Is Not an Electric Calendar App, but a Typst package to create calendars with events.
Example:

## Usage
`calendar(events, hour-range, minute-height, template, stroke)`
Parameters:
- `events`: An array of events. Each item is a 4-element array:
- Index of day. Start from 0.
- Float-style start time.
- Float-style end time.
- Event body. Can be anything. Passed to the template.body to show more details.
- `hour-range`: Then range of hours, affacting the range of the calendar. Default: `(8, 20)`.
- `minute-height`: Height of per minute. Each minute occupys a row. This number is to control the height of each row. Default: `0.8pt`.
- `template`: Templates for headers, times, or events. It takes a dictionary of the following entries: `header`, `time`, and `event`. Default: `(:)`.
- `stroke`: A stroke style to control the style of the default stroke, or a function taking two parameters `(x, y)` to control the stroke. The first row is the dates, and the first column is the times. Default: `none`.
> Float-style time means a number representing 24-hour time. The integer part represents the hour. The fractional part represents the minute.
## Limitations
- Page breaking may be incorrect.
- Items will overlap when they happens at the same time.
|
https://github.com/adambarla/HIV-protease-binding | https://raw.githubusercontent.com/adambarla/HIV-protease-binding/main/report/report.typ | typst | #import "template.typ" : *
#show : ieee.with(
title: [
Molecular Docking and Molecular Dynamics Simulations of Ligands Against HIV-1 Protease
],
// abstract: [
// ],
authors: (
(
name: "<NAME>",
department: [BS7107],
location: [NTU, Singapore],
email: "<EMAIL>"
),
),
// index-terms: ("A", "B", "C", "D"),
// bibliography-file: "refs.bib",
)
#show link: set text(blue)
#show link: underline
= Introduction
#figure(
placement: bottom,
pad(16pt, image("figures/saquinavir_nglview.png", width: 100%)),
caption: [Saquinavir],
) <saquinavir>
Molecular docking is a computational technique used to predict the binding mode of a ligand to a protein target.
It is a crucial step in drug discovery, as it can help identify potential drug candidates.
In this report, I describe the computational methods used to perform molecular docking and molecular dynamics simulations on a dataset of ligands against a protein target.
The ligands were docked against the #link("https://www.rcsb.org/structure/4qgi")[HIV-1 protease] variant G48T/L89M protein seen in @hiv1.
HIV-1 protease is an enzyme that plays a crucial role in the replication of the human immunodeficiency virus (HIV).
It cleaves the newly synthesized polyproteins into mature protein components of an HIV virion -- the infectious form of a virus outside the host cell.
The docking was performed using #link("https://github.com/QVina")[`QuickVina`] and the ligand with the best fit was selected for molecular dynamics simulation done using #link("https://github.com/gromacs")[`GROMACS`].
The simulation was carried out a second time, this time with #link("https://en.wikipedia.org/wiki/Saquinavir")[Saquinavir] (seen in @saquinavir), a known inhibitor of the HIV-1 protease.
Both ligands were compared in terms of their Root-Mean-Square Deviation (RMSD) and other properties to determine the quality of the fit and the potential of the new ligand as a drug candidate.
#figure(
placement: top,
image("figures/hiv1_nglview.png", width: 90%),
caption: [HIV-1 protease variant G48T/L89M]
) <hiv1>
= Methods
Before performing MD I selected the ligand with the best fit from the docking results.
I used a dataset of $2116$ ligands to dock against the HIV-1 protease.
All files and scripts used in this project can be found on `github` at #link("https://github.com/adambarla/HIV-protease-binding")[`adambarla/HIV-protease-binding`].
== Molecular Docking
I downloaded the X-ray crystal structure of HIV-1 protease variant G48T/L89M in complex with Saquinavir from #link("https://www.rcsb.org/structure/4qgi")[`rcsb`] in a single PDB file.
Before separating the ligand from the protein, I accessed the middle atoms of the Saquinavir which was positioned inside the Protease from the start. I looked at the distances to surrounding protein which can be seen in @distances in the appendix. Based on these distances, I selected an atom that was the nearest to the surrounding protein. The coordinates of this atom were used as the center of the bounding box for the docking simulation. Parameters for the docking were set as follows:
#box(
height: 3em,
columns(2)[
#set align(center)
```toml
center_x = 21.877
center_y = -0.510
center_z = 11.108
size_x = 20
size_y = 20
size_z = 20
```
]
)
I then split the molecule into two files `saquinavir.pdb` and `hiv1.pdb` and prepared them using `prepare_receptor` and `prepare_ligand` from the #link("https://ccsb.scripps.edu/adfr/")[ADFR Suite].
== Selecting a ligand with the best fit
I used a `python` code, which can be found in the `notebook.ipynb`, to parse the `qvina` output files and extract the most negative binding affinity score for each ligand out of $2116$ tested.
This involved identifying lines containing the `"REMARK VINA RESULT"` and capturing the first numerical value (the binding
affinity score).
The top $10$ best ligands selected can be seen in the @best_fits.
The two top ones (`fda_553` and `fda_554`) are just variations of Saquinavir with some additional hydrogen atoms.
I decided to select the ligand with the third lowest binding affinity score named `fda_1700` and it can be seen in @best_ligand.
I was able to find the ligand in the ZINC database by converting it to SMILES format with the following command:
```bash
obabel -ipdbqt fda_pdbqt/fda_1700.pdbqt \
-osmi -O fda_1700.smi
```
The ligand `fda_1700` corresponds to the one with the zinc id #link("https://zinc.docking.org/substances/ZINC001560410173/")[ZINC001560410173] in the database.
#figure(
placement: bottom,
pad(16pt, image("figures/best_ligand.png", width: 100%)),
caption: [
Ligand name `fda_1700` in the dataset. Ligand's ZINC ID is ZINC001560410173. It has reached the third lowest binding affinity score of $-11.1$ kcal/mol out of $2116$ ligands tested.
],
) <best_ligand>
The ligand's binding affinity score was $-11.1$ kcal/mol which is slightly less than Saquinavir's $-11.4$ kcal/mol.
#figure(
placement: top,
[
#show table.cell.where(x: 10): set text(weight: "bold",)
#set text(size: 9pt,)
#table(
stroke: none,
columns: (40pt, auto, auto, auto, auto, auto, auto, auto, auto, auto, auto),
align: (horizon, center),
table.hline(start: 0,stroke:1pt),
table.header(
table.cell(rowspan:2,[*Ligand*]), table.cell(colspan: 9, [*Model*]), table.cell(rowspan:2, [*min*]),
table.hline(start: 0,stroke:0.5pt),
[1], [2], [3], [4], [5], [6], [7], [8], [9],
),
table.hline(start: 0),
..csv("figures/best_fits.csv").flatten(),
table.hline(start: 0,stroke:1pt),
)
],
caption: [Top $10$ ligands with the lowest minimal (out of all models tested) binding affinity score],
) <best_fits>
== Molecular dynamics
In this section, I outline the sequence of computational steps taken to prepare a molecular system for dynamic simulation using `GROMACS`.
Initially, I converted the ligand's structural data from `PDBQT` to `PDB` format with _Open Babel_, separating molecules and adding hydrogen atoms.
Next, `Antechamber` was used to generate a `MOL2` file, calculating `AM1-BCC` charges and setting the net charge and multiplicity.
The `parmchk2` command then created a force field modification file for missing parameters.
With `tleap`, I prepared the system using the `ff14SB` force field, incorporating ligand parameters.
The final step involved the `parmed_amber2gmx.py` script (see `scripts` folder) to convert `AMBER` files to `GROMACS` format.
Following the successful setup of the ligand, I applied the `tleap` and `parmed_amber2gmx.py` steps to prepare the protein component.
=== Solvation of the system
I then combined the ligand and protein systems into a single `GROMACS` input file `sys.gro` while making sure that the information about atom types and molecules was correct.
I created a box around the system using the `editconf` command with a buffer of $1.0$ nm around the centered protein-ligand complex.
I solvated the system with water molecules around the molecule in the bounding box creating a `wat.gro` file.
I used `configs/spc903.gro` as the solvent configuration.
The topology file `sys.top` was updated with the number of solvent molecules added.
Next preprocessing step was to compile the system topology from `sys.top`, the solvated configuration from `wat.gro` with `gmx grompp` using minimization parameters from `configs/mini.mdp`, to generate a portable binary run file `bions.tpr`.
Then I neutralize the system with `gmx genion` command which replaces solvent molecules with ions to reach a desired ionic concentration of $0.15$ mol/l. The topology `sys.top` was again updated with the ion information, and the output configuration is saved as `ions.gro`.
I also added water molecules to the system together with Na and Cl ions to neutralize the system.
=== Energy minimization
After solvation, I combined the `ions.gro` and `sys.top` files to create a portable binary run file `mini.tpr` with `gmx grompp` using the `mini.mdp` parameters.
I performed energy minimization of the system using the `gmx mdrun` command with the `mini.tpr` created by the previous step.
=== Running the simulation
I created an index file `index.ndx` with `gmx make_ndx`.
Using `configs/pr.mdp` parameters, I created a portable binary run file `pr.tpr` with `gmx grompp` to run the position restrained simulation which was done with `gmx mdrun`.
Using `configs/md.mdp` parameters, I created a portable binary run file `md001.tpr` with `gmx grompp` to run the production simulation which was done with `gmx mdrun`.
Finally, I ran the production simulation with `gmx mdrun` using the `configs/md.mdp` parameters.
The simulation was run for $5000000$ steps totaling $10$ ns and it was repeated with Saquinavir as the ligand.
= Results
I analyzed the results of the molecular dynamics simulations to compare the ligands in terms of their stability and conformational changes over time.
== Root-Mean-Square Deviation (RMSD)
#figure(
placement: bottom,
image("figures/rmsd.svg", width: 100%),
caption: [
Root-Mean-Square Deviation (RMSD) of a ligand after performing a least squares fit to a protein over time in a molecular dynamics simulation.
The figure shows a comparison of the RMSD of Saquinavir and the ligand `fda_1700`.
]
) <rmsd>
RMSD is used to measure the average distance between atoms of superimposed structures.
It is a commonly used metric to assess the conformational stability and structural changes of a macromolecule (protein) over time during a simulation.
Lower RMSD values indicate higher structural stability. During the initial phase of the simulation, the RMSD will typically increase rapidly as the system departs from the starting structure. Once equilibrated, the RMSD will plateau, indicating that the system is sampling around an average structure.
I calculated the RMSD (root mean squared deviation) to check how far the peptide
structure changes from the initial one.
The comparison of RMSD for the ligand `fda_1700` and Saquinavir over time can be seen in @rmsd.
== Radius of Gyration ($R_g$)
The radius of gyration is a measure that describes the distribution of components (such as atoms) around the center of mass of a molecule.
It gives us an idea of the molecule's "compactness" and can inform us about its three-dimensional structure.
$R_g$ is calculated using the positions of all the atoms in the molecule, weighted by their masses.
Mathematically, it is defined as the root-mean-square distance of the system's parts from its center of mass.
The comparison of $R_g$ of the protein when simulated with the ligand `fda_1700` and Saquinavir over time can be seen in @rg.
#figure(
placement: top,
image("figures/md_gyr_hiv.svg", width: 100%),
caption: [
The radius of gyration ($R_g$) of the protein when simulated with the ligand `fda_1700` and Saquinavir over time.
]
) <rg>
== Root-Mean-Square Fluctuation (RMSF)
Root Mean Square Fluctuation (RMSF) measures the deviation of positions of a selection of atoms (usually the backbone atoms) over time from a reference position (often the time-averaged position). It's used to understand the flexibility and dynamics of a molecule or molecular complex within a simulation.
Calculating RMSF per residue gives insight into which parts of the protein are more flexible or rigid during the simulation.
High RMSF values indicate regions with high flexibility, while low RMSF values indicate more rigid, stable regions.
This can help identify flexible loops, stable cores, or regions that undergo conformational changes in response to ligand binding or other factors.
The comparison of RMSF for the protein when simulated with the ligand `fda_1700` and Saquinavir over time can be seen in @rmsf_saq and @rmsf_fda in the appendix.
The most mobile regions for protein with `fda_1700` are residues $41$, $53$, $51$, and $50$. While for protein with Saquinavir, the most mobile regions are residues $41$, $17$, $69$, $18$, and $16$. Positions of these residues can be seen in the @hiv1_res.
#figure(
placement: bottom,
image("figures/hiv1_residues.png", width: 100%),
caption: [HIV-1 protease variant G48T/L89M with residues that have the highest RMSF values marked.]
) <hiv1_res>
== Radial Distribution Function (RDF)
The Radial Distribution Function (RDF) is a measure of the probability of finding a particle at a distance $r$ from a reference particle. Function $g(r)$ measures how density varies as a function of distance from a reference particle.
If $g(r) = 1$, it means that particles are distributed at that distance in a completely random, homogeneous manner, as expected in an ideal gas or the bulk phase of a liquid.
A hydration shell is a layer of water molecules that surrounds a solute when it's dissolved in water.
This interaction of the protein surface with the surrounding water is often referred to as protein hydration and is fundamental to the activity of the protein.
Solvation shell water molecules can also influence the molecular design of protein binders or inhibitors.
I calculated the RDF for the protein with `fda_1700` and Saquinavir to compare the distribution of water molecules around the heavy atoms of the protein (not including hydrogen atoms).
The RDF plots with the distribution of water molecules around the protein with `fda_1700` and Saquinavir and highlighted peaks can be seen in @rdf.
#figure(
placement: top,
image("figures/rdf_p_ow.svg", width: 100%),
caption: [
The Radial Distribution Function (RDF) graph shows how the density of water molecules varies as a function of distance from the protein complexed with two different ligands: `fda_1700` and Saquinavir.
The $x$-axis is the distance from the protein in nanometers on a logarithmic scale, and the $y$-axis is the $g(r)$, a measure of density relative to bulk water.
Vertical lines highlight peaks in the RDF plot.
]
) <rdf>
= Discussion
== RMSD
Looking at @rmsd, the `fda_1700` simulation shows significant initial conformational changes, as evidenced by the initial rise in RMSD. It stabilizes somewhat but continues to fluctuate throughout the simulation, suggesting this structure is more flexible or undergoes conformational changes during the simulation.
The `saquinavir` line shows much lower RMSD values, which remain relatively stable throughout the simulation.
This suggests that `saquinavir` maintains a more stable conformation compared to `fda_1700` during the same simulation timeframe.
== Radius of Gyration
Comparison of $R_G$ in @rg shows that the protein with the `fda_1700` ligand starts with a larger $R_g$, which might indicate it initially adopts a more expanded conformation that is less stable or allows greater flexibility in the protein structure than when bound to Saquinavir.
However, towards the end, the drop in $R_g$ for `fda_1700` below Saquinavir's could indicate that the protein-ligand complex has reached a stable conformation after undergoing necessary conformational adjustments.
== RMSF
The RMSF plots in @rmsf_saq and @rmsf_fda show that the protein with `fda_1700` has more pronounced fluctuations,
with some very high peaks, indicating regions of significant flexibility. This might suggest that the fda_1700 ligand causes some regions of the protein to be more dynamic.
The RMSF values are generally lower for the protein with Saquinavir, implying the protein is overall less flexible with this ligand.
The lower peaks suggest more rigidity or a stable conformation.
Interestingly, the residues with the highest RMSF values differ between the two simulations. From the @hiv1_res, we can see that the most mobile regions for protein with Saquinavir are on the surface of the protein, while for protein with `fda_1700`, they are more towards the core of the protein (near the binding site). This could mean that the `fda_1700` ligand doesn't bind as tightly to the protein as Saquinavir, leading to more flexibility in the core regions.
== RDF
The RDF plots in @rdf show the distribution of water molecules around the protein with `fda_1700` and Saquinavir.
For both ligands, there's a notable increase in water density at certain distances from the protein, which could indicate preferred distances where water molecules are more likely to be found due to interactions with the protein-ligand complex. Peaks and troughs represent areas of higher and lower water molecule density, respectively.
The lines for "fda_1700" and "saquinavir" track closely together, suggesting similar hydration patterns for both ligands when bound to the protein. Differences in the lines could indicate differences in how water molecules interact with and organize around the different ligands.
If Saquinavir fills the binding "hole" in the protein better than `fda_1700`, it may displace more water molecules from the cavity, resulting in a lower RDF, which we observe in the plot. This could indicate a tighter binding of Saquinavir to the protein compared to `fda_1700`.
= Conclusion
In this report, I described the computational methods used to perform molecular docking and molecular dynamics simulations of ligands against the HIV-1 protease variant G48T/L89M.
I selected the ligand `fda_1700` with the lowest binding affinity score (aside from Saquinavir variants) from the docking results and compared it to Saquinavir in terms of RMSD, $R_g$, RMSF, and RDF.
The results suggest that the protein with `fda_1700` undergoes more conformational changes and has higher flexibility compared to Saquinavir.
The higher RMSD, $R_g$, and RMSF values for `fda_1700` indicate that it may not bind as tightly to the protein as Saquinavir, leading to more flexibility in the core regions of the protein.
The RDF plots show similar hydration patterns for both ligands, but differences in water density around the protein could indicate differences in how water molecules interact with the protein-ligand complex.
Overall, the results suggest that Saquinavir may be a more stable and tightly bound ligand compared to `fda_1700`, which was expected given Saquinavir's known inhibitory activity against the HIV-1 protease.
#colbreak()
#set heading(numbering: "1.")
#counter(heading).update(0)
= Appendix
#figure(
image("figures/distances_nglview.png", width: 90%),
caption: [Distances between the center atom `A/ROC100/O2A` of the Saquinavir and surrounding atoms of the Protease.]
) <distances>
#figure(
image("figures/rmsf_hiv_res_saq.svg", width: 100%),
caption: [
Root-Mean-Square Fluctuation (RMSF) of the protein when simulated with the Saquinavir over time.
]
) <rmsf_saq>
#figure(
image("figures/rmsf_hiv_res_fda.svg", width: 100%),
caption: [
Root-Mean-Square Fluctuation (RMSF) of the protein when simulated with the ligand `fda_1700` over time.
]
) <rmsf_fda> |
|
https://github.com/Jollywatt/typst-fletcher | https://raw.githubusercontent.com/Jollywatt/typst-fletcher/master/docs/gallery/digraph.typ | typst | MIT License | #import "@preview/fletcher:0.5.1" as fletcher: diagram, node, edge, shapes
#set page(width: auto, height: auto, margin: 5mm, fill: white)
#let nodes = ("A", "B", "C", "D", "E", "F", "G")
#let edges = (
(3, 2),
(4, 1),
(1, 4),
(0, 4),
(3, 0),
(5, 6),
(6, 5),
)
#diagram({
for (i, n) in nodes.enumerate() {
let θ = 90deg - i*360deg/nodes.len()
node((θ, 18mm), n, stroke: 0.5pt, name: str(i))
}
for (from, to) in edges {
let bend = if (to, from) in edges { 10deg } else { 0deg }
// refer to nodes by label, e.g., <1>
edge(label(str(from)), label(str(to)), "-|>", bend: bend)
}
}) |
https://github.com/vEnhance/1802 | https://raw.githubusercontent.com/vEnhance/1802/main/src/gcd.typ | typst | MIT License | #import "@local/evan:1.0.0":*
= Grad, curl, and div, individually
#pagebreak()
|
https://github.com/jens-hj/ds-exam-notes | https://raw.githubusercontent.com/jens-hj/ds-exam-notes/main/lectures/14.typ | typst | #import "../lib.typ": *
#show link: it => underline(emph(it))
#set math.equation(numbering: "(1)")
#set enum(full: true)
#set math.mat(delim: "[")
#set math.vec(delim: "[")
#set list(marker: text(catppuccin.latte.lavender, sym.diamond.filled))
#show heading.where(level: 1): it => text(size: 22pt, it)
#show heading.where(level: 2): it => text(size: 18pt, it)
#show heading.where(level: 3): it => {
text(size: 14pt, mainh, pad(
left: -0.4em,
gridx(
columns: (auto, 1fr),
align: center + horizon,
it, rule(stroke: 1pt + mainh)
)
))
}
#show heading.where(level: 4): it => text(size: 12pt, secondh, it)
#show heading.where(level: 5): it => text(size: 12pt, thirdh, it)
#show heading.where(level: 6): it => text(thirdh, it)
#show emph: it => text(accent, it)
#show ref: it => {
//let sup = it.supplement
let el = it.element
if el == none {
it.citation
}
else {
let eq = math.equation
// let sup = el.supplement
if el != none and el.func() == eq {
// The reference is an equation
let sup = if it.fields().at("supplement", default: "none") == "none" {
[Equation]
} else { [] }
// [#it.has("supplement")]
show regex("\d+"): set text(accent)
let n = numbering(el.numbering, ..counter(eq).at(el.location()))
[#sup #n]
}
else if it.citation.has("supplement") {
if el != none and el.func() == eq {
show regex("\d+"): set text(accent)
let n = numbering(el.numbering, ..counter(eq).at(el.location()))
[#el.supplement #n]
}
else {
text(accent)[#it]
}
}
}
}
=== Definition of Secure
- CIA
==== CIA(A)
- *Confidentiality* \
#ra Protect against eavesdropping (Encryption)
- *Integrity* \
#ra Protect against tampering
- *Availability* \
#ra Protect against denial of service
- *Authenticity* \
#ra Protect against impersonation
=== How to make it Secure
- Security engineering
- Each system has its own security threats and thus requirements
- Identify the threats and requirements
- Design the system to meet the requirements
- Arms race
==== Swiss cheese problem
*Each layer has holes*
- Holes are not aligned
- Holes are not the same size
*Add more layers*
- Some threats are covered by many layers
- Some threats are covered by only a few layers
=== Summary
- Security has to be tailored to the concrete system
- Identify threats and associated risks before thinking of countermeasures
- Learn and use best practices
- Do not invent new cryptography
- Make sure that different security techniques are not working against each other
- Consider data lifecycle and keep backwards-compatibility open
==== Accountability
- Actions of an entity can be traced uniquely to that entity
- *Why is it important?*
- Important nodes may be vulnerable to other attacks if discovered
- Maybe the attacker has identified the _most important_ node |
|
https://github.com/yochem/apa-typst | https://raw.githubusercontent.com/yochem/apa-typst/main/template.typ | typst | #let fontsize = state("fontsize", 0pt)
#let doublespace = 1.7em
#let authorHasOrcid(authors) = authors.map(author =>
// if type(author) == dictionary and dictHasKey(author, "orcid") {
if type(author) == dictionary and "orcid" in author {
true
} else {
false
}
).contains(true)
#let differentAffiliations(authors) = authors.map(author =>
if type(author) == dictionary and "affiliations" in authors {
true
} else {
false
}
).contains(true)
#let apa7(
title: "",
running-head: none,
date: datetime.today(),
authors: ("",),
affiliations: none,
keywords: none,
abstract: none,
titlepage-type: "professional",
authornote: none,
footnotepage: false,
body
) = {
let warning = text.with(red, weight: "bold")
show par: set block(spacing: doublespace) // §2.24
// §2.18
let header = upper({
let rh = if running-head != none {
running-head
} else {
title
}
if rh.len() > 50 {
warning[running-head too long]
} else {
rh
}
h(1fr)
counter(page).display()
})
let authorNames = authors.map(it =>
if type(it) == str {
it
} else {
it.name
}
)
set document(
author: authorNames,
title: title,
date: date
)
set text(
hyphenate: false // §2.23
)
set page(
numbering: "1",
paper: "a4",
header: header,
header-ascent: 3em,
footer: "",
margin: (top: 1in + doublespace, rest: 1in), // §2.22
)
set par(first-line-indent: 0.5in, leading: doublespace) // §2.21
// set font size, used for headings
style(styles => {
fontsize.update(measure(v(1em), styles).height)
})
// §2.27
show heading: it => {
block(below: 0em, text(fontsize.at(it.location()), weight: "bold")[#it.body])
par(text(size:0.35em, h(0.0em)))
}
show heading.where(level: 1): align.with(center)
show heading.where(level: 3): text.with(style: "italic")
show heading.where(level: 4): it => {
box(it.body + [.])
}
show heading.where(level: 5): it => {
set text(style: "italic")
box(it.body + [.])
}
show footnote.entry: it => if not footnotepage { it }
set footnote.entry(separator: if not footnotepage { line(length: 30%, stroke: 0.5pt) })
show figure: it => {
block({
// TODO: sans-serif font
text(weight: "bold")[
#it.supplement
#counter(figure.where(kind: it.kind)).display()
]
block(emph(it.caption.body))
it.body
})
}
show table: set par(hanging-indent: 0.15in)
set bibliography(title: "References")
show bibliography: it => {
set par(hanging-indent: 0.5in)
pagebreak(weak: true)
it
}
// §8.26-27
show quote: it => {
if it.body.has("text") and it.body.text.split().len() <= 40 {
it
} else {
pad(left: 0.5in, {
// for para in it.body.children {
// par(first-line-indent: 0.5in, para)
// }
it.body
})
}
}
// title page
page({
set align(center)
v(4 * doublespace)
block(spacing: 2em,
text(weight: "bold", [
#title
]
))
hide(par[empty line])
// §2.6
let showAuthors = authors.map(it => {
if type(it) == dictionary {
it.name + super(it.at("affiliations", default: ()).sorted().map(str).join(","))
} else {
it
}
})
// §2.5
if authors.len() == 1 {
showAuthors.first()
} else if authors.len() == 2 {
showAuthors.join(" and ")
} else {
showAuthors.join(", ", last: ", and ")
}
// §2.6
if affiliations != none {
parbreak()
// include marks if authors have different affiliations
let affiliationsWithMark = if differentAffiliations(authors) {
affiliations.enumerate(start: 1).map(it =>
[#super([#it.first()]) #it.last()]
)
} else {
affiliations
}
for affiliation in affiliationsWithMark {
par(affiliation)
}
}
v(1fr)
// §2.7
if authorHasOrcid(authors) {
par(text(weight: "bold")[Author Note])
set align(left)
for author in authors {
if "orcid" in author {
let url = "https://orcid.org/" + author.orcid
par[
#author.name
#box(image("orcid-logo.svg", height: 0.8em))
#url
]
}
}
}
})
if abstract != none {
show heading: it => {
align(center, block(above: doublespace, below: doublespace, {
text(fontsize.at(it.location()), weight: "bold")[#it.body]
}))
}
heading(level: 1, supplement: [Abstract], "Abstract")
abstract
parbreak()
if keywords != none {
text(style: "italic")[Keywords: ]
keywords.join(", ")
}
pagebreak()
}
heading(level: 1, title)
body
}
// 2.13
#let showfootnotes = {
pagebreak(weak: true)
[= Footnotes]
set par(first-line-indent: 0.5in)
locate(loc => {
for (i, note) in query(footnote, loc).enumerate(start: 1) {
par[#super[#i] #note.body #lorem(20)]
}
})
}
#let appendix(body) = {
pagebreak()
show heading.where(supplement: [Appendix], level: 1): it => {
pagebreak(weak: true)
align(center, block(above: doublespace, below: doublespace, {
text(fontsize.at(it.location()), weight: "bold")[
#it.supplement
#if it.numbering != none [
#counter(heading).display()\
#it.body
]
]
}))
counter(figure.where(kind: table)).update(0)
counter(figure.where(kind: image)).update(0)
counter(math.equation).update(0)
}
set heading(supplement: "Appendix", numbering: "A1")
locate(loc => {
let appendixSectionCount = query(selector(
heading.where(supplement: [Appendix])
).after(loc), loc).len()
if appendixSectionCount == 0 {
heading(supplement: [Appendix], numbering: none, "")
}
})
let numberByChapter(obj) = locate(loc => {
let chapter = numbering("A", ..counter(heading).at(loc))
[#chapter#numbering("1", obj)]
})
set figure(numbering: n => numberByChapter(n))
set math.equation(numbering: n => numberByChapter(n))
body
}
|
|
https://github.com/DashieTM/ost-5semester | https://raw.githubusercontent.com/DashieTM/ost-5semester/main/patterns/gg.typ | typst | #set page("a4", columns: 4, flipped: true, margin: 5pt )
#set columns(gutter: 0pt)
#image(fit: "contain", height: 80pt, "images/image1.png")
#image(fit: "contain", height: 80pt, "images/image2.png")
#image(fit: "contain", height: 80pt, "images/image3.jpeg")
#image(fit: "contain", height: 80pt, "images/image4.png")
#image(fit: "contain", height: 80pt, "images/image5.jpeg")
#image(fit: "contain", height: 80pt, "images/image6.png")
#image(fit: "contain", height: 80pt, "images/image7.jpeg")
#image(fit: "contain", height: 80pt, "images/image8.png")
#image(fit: "contain", height: 80pt, "images/image9.png")
#image(fit: "contain", height: 80pt, "images/image10.png")
#image(fit: "contain", height: 80pt, "images/image11.png")
#image(fit: "contain", height: 80pt, "images/image12.png")
#image(fit: "contain", height: 80pt, "images/image13.png")
#image(fit: "contain", height: 80pt, "images/image14.png")
#image(fit: "contain", height: 80pt, "images/image15.png")
#image(fit: "contain", height: 80pt, "images/image16.jpeg")
#image(fit: "contain", height: 80pt, "images/image17.jpeg")
#image(fit: "contain", height: 80pt, "images/image18.jpeg")
#image(fit: "contain", height: 80pt, "images/image19.png")
#image(fit: "contain", height: 80pt, "images/image20.png")
#image(fit: "contain", height: 80pt, "images/image21.jpeg")
#image(fit: "contain", height: 80pt, "images/image22.png")
#image(fit: "contain", height: 80pt, "images/image23.jpeg")
#image(fit: "contain", height: 80pt, "images/image24.jpeg")
#image(fit: "contain", height: 80pt, "images/image25.jpeg")
#image(fit: "contain", height: 80pt, "images/image26.png")
#image(fit: "contain", height: 80pt, "images/image27.jpeg")
#image(fit: "contain", height: 80pt, "images/image28.png")
#image(fit: "contain", height: 80pt, "images/image29.jpeg")
#image(fit: "contain", height: 80pt, "images/image30.png")
#image(fit: "contain", height: 80pt, "images/image31.jpeg")
#image(fit: "contain", height: 80pt, "images/image32.png")
#image(fit: "contain", height: 80pt, "images/image33.jpeg")
#image(fit: "contain", height: 80pt, "images/image34.jpeg")
#image(fit: "contain", height: 80pt, "images/image35.png")
#image(fit: "contain", height: 80pt, "images/image36.png")
#image(fit: "contain", height: 80pt, "images/image37.jpeg")
#image(fit: "contain", height: 80pt, "images/image38.png")
#image(fit: "contain", height: 80pt, "images/image39.jpeg")
#image(fit: "contain", height: 80pt, "images/image40.png")
#image(fit: "contain", height: 80pt, "images/image41.png")
#image(fit: "contain", height: 80pt, "images/image42.png")
#image(fit: "contain", height: 80pt, "images/image43.png")
#image(fit: "contain", height: 80pt, "images/image44.png")
#image(fit: "contain", height: 80pt, "images/image45.png")
|
|
https://github.com/Area-53-Robotics/53E-Notebook-Over-Under-2023-2024 | https://raw.githubusercontent.com/Area-53-Robotics/53E-Notebook-Over-Under-2023-2024/giga-notebook/entries/auton-routes/decide.typ | typst | Creative Commons Attribution Share Alike 4.0 International | #import "/packages.typ": notebookinator, codetastic
#import notebookinator: *
#import themes.radial.components: *
#import codetastic: qrcode
#show: create-body-entry.with(
title: "Decide: Autonomous Routes",
type: "decide",
date: datetime(year: 2023, month: 12, day: 1),
author: "<NAME>",
witness: "<NAME>",
)
= Match Autons
After identifying that AWP #footnote[See Glossary] is the most important thing
we can accomplish during the autonomous period, we need some routes to follow.
We cannot do all the AWP tasks ourselves because they require us to be on both
sides of the field. This means that we'll have to prepare two different
autonomous routines, one for each side of the field. We used a piece of software
called PATH.JERRYIO #footnote(qrcode("https://github.com/Jerrylum/path.jerryio", size: 2pt)) to
plan all of our routes.
#grid(
columns: (1fr, 1fr),
gutter: 20pt,
[
== Offensive
The offensive side route performs two tasks: scoring the alliance triball, and
touching the elevation bar. First we move forward, and then we turn to face the
goal. We push our preloaded triball into the goal. Once this is done, we drive
over to the barrier, and extend our flaps to touch the bar.
],
image("./offensive.png"),
image("./defensive.png"),
[
== Defensive
The defensive side auton is slightly more complicated. It performs two of the
AWP tasks, and scores an alliance triball in the opposing goal.
#admonition(
type: "note",
)[
Even though we are scoring a triball in this auton, this does not count as a
solo AWP, because the rules stipulate that the goal must be our alliance goal.
]
],
)
= Skills Auton
The skills autonomous route is much more complex than the other two, since it
lasts for a whole minute. Our strategy is to shoot all of our match loads, and
then attempt to push as many of the triballs into the goal as possible.
#image("./skills.png", width: 70%)
We first move to the match load bar, and then delay until all of the triballs
have been fired. Once we do that we move across the entire field, expand our
wings, and drive against the goal. At this point there will be so many triballs
on that side of the field that we are almost guaranteed to get some into the
goal, especially the extra reach our wings give us. We repeat this motion a
second time on the front of the goal.
|
https://github.com/DieracDelta/presentations | https://raw.githubusercontent.com/DieracDelta/presentations/master/polylux/book/src/utils/fit-to-height.md | markdown | # Fit to height
Suppose you have some content and some size constraints for it but the two don't
match, i.e. the content does not have the size that you want.
The function `#fit-to-height` can help you with that.
It expects a height and some content and will try to scale the content such that
it takes on the given height:
```typ
{{#include fill-remaining.typ:6}}
```
resulting in

Using `1fr` as the height is probably also the prime use case for this function,
as it fills the remaining space of the slide with the given content.
Anything else (like `5pt`, `3cm`, `4em` etc.) is possible as well, of course.
## Adjusting the width
To finetune the result of `#fit-to-height`, you have two optional parameters:
- `width`: If specified, this determines the width of the content _after_ scaling.
So, if you want the scaled content to fill half the slide's width for example,
you can use `width: 50%`.
By default, the scaled content will be constrained by the slide's width and
will have less than the requested height if necessary.
- `prescale-width`: This parameter allows you to make Typst's layouting assume
the given content is to be layouted in a container of a certain width _before_
scaling.
You can pretend the slide is twice as wide using `prescale-width: 200%`, for
example.
We can illustrate that using the following example:
```typ
{{#include fit-to-height-width.typ:6:9}}
```
resulting in

|
|
https://github.com/PA055/5839B-Notebook | https://raw.githubusercontent.com/PA055/5839B-Notebook/main/Entries/First-Steps/first-steps.typ | typst | #import "/packages.typ": notebookinator
#import notebookinator: *
#import themes.radial.components: *
#show: create-body-entry.with(
title: "First Steps",
type: "decide",
date: datetime(year: 2024, month: 3, day: 9),
author: "<NAME>",
witness: "<NAME>"
)
= Post Season Build Analysis
For the building of our previous robot even though it unfortunately did not make worlds there were a lot of aspects executed properly and poorly to be identified. This is important as it allows the team to know what works and to keep doing as well as what to change in order to improve for the next season.
*Drive Train* The Drive Train is the base of any robot. The previous seasons drive train used 6 11w motors with the blue cartidge and a 48:60 gear ratio giving an RPM of 480. This spun 3 4" omni wheels with the middle one on each side being locked.
#pro-con(
pros: [
- Speed
- Pushing power
- Strong Wedge
],
cons: [
- Turning
- Reliability
- Over Heating
- Field Traversal
]
)
*Intake* The intake was powered by 1 5.5w motor spining a series of 2" 45A flexwheels to interact with the game objects. The intake was also allowed to float so that it could raise over the goal to score the triball.
#pro-con(
pros: [
- Holding ability
- Scoring
- Reliability
- Effectiveness
],
cons: [
- Chain Broke once
]
)
*Wings* These were pneumatically activated flaps that would extend 9in on either side of the robot. These allowed for a large amount of game objects to be pushed into the goal at one time.
#pro-con(
pros: [
- Never failed
- Reached corners
- Simple Design
],
cons: [
- Bent after multiple matches
]
)
*Flywheel Arm* this was a 4" Flexwheel with a ratchet spining at 3600 RPM off of a blue motor. Game obejcts were placed and laumched off of the flywheel. It could also be raised by a 5.5w motor assisted by rubber bands to shoot over other robots.
#pro-con(
pros: [
- Consistent firing
- Fast firing
- Height
- Ratchet persrved motor health
],
cons: [
- Unable to use the arm for climbing
- Flywheel got jammed on a standoff in 2 matches
]
)
*Odometry Modules* These are 3 modules 2 vertical and 1 horizantal that are used to track the robots position. They are jointed to always be in contact with the ground, and have a 3.25" omni wheel spin an encoder to track movements.
#pro-con(
pros: [
- Simple Design
],
cons: [
- Bent over time
- Large
- Unreliable gorund contact
]
)
= What to do now?
- With the biggest problem being the drive a variety of drives should be modeled and tested in order to have a better idea of what works for the next season
- Work to create new odometry module desings that are stronger and more compact
- Take inventory of the parts available to our team so that when designing we know what parts we can use and how many of them are available
- Put together an order list of parts that the team wants to asses the needed funds
- See what funding is available to the team and what amount should be allocated to new parts
- Look into making a functional PTO (power take off) as they can allow for more powerful drives while still having all the desired mechanisms to manipulate game objects
- Look for or model our own paddels for the controller that suite the needs of our driver
|
|
https://github.com/typst/packages | https://raw.githubusercontent.com/typst/packages/main/packages/preview/crossregex/0.1.0/README.md | markdown | Apache License 2.0 | # crossregex
A crossword-like game written in Typst. You should fill in letters to satisfy regular expression constraints.
It takes inspiration from a web image, which derives our standard example.

More examples and source code: <https://github.com/QuadnucYard/crossregex-typ>
## Notations
### Constraint hints
In front of each regex constraint text, we have a circle in red, yellow or green. It has the following meaning:
- $\color{red}\text{Red}$: This constraint is not satisfied.
- $\color{yellow}\text{Yellow}$: This constraint is satisfied, but unfilled cells exist.
- $\color{green}\text{Green}$: This constraint is satisfied.
We use a wasm plugin to check matching.
### Filled letters
In the hex grids, upper-case letters are colored $\color{blue}\text{blue}$, while others are colored $\color{purple}\text{purple}$. So you can use lower-case letters or symbols as hints.
### Counting
If you provide answers, it will show the number of filled and total cells at bottom left.
## Basic Usage
```typst
#import "@preview/crossregex:0.1.0"
#crossregex(
3,
constraints: (
`A.*`, `B.*`, `C.*`, `D.*`, `E.*`,
`F.*`, `G.*`, `H.*`, `I.*`, `J.*`,
`K.*`, `L.*`, `M.*`, `N.*`, `O.*`,
),
answer: (
"ABC",
"DEFG",
"HIJKL",
"MNOP",
"QRS",
),
)
```
Maybe triangle and square grids can be added later.
## Documentation
See the doc comments above the `crossregex` function in `crossregex.typ`.
You can choose to turn off some views.
|
https://github.com/juraph-dev/usyd-slides-typst | https://raw.githubusercontent.com/juraph-dev/usyd-slides-typst/main/README.md | markdown | MIT License | # usyd-slides-typst

Polylux slide template for University of Sydney themed presentations.
Almost a direct translation of [usyd-beamer-theme](https://github.com/malramsay64/usyd-beamer-theme) to Typst, with one of two adjustments for taste.
Uses the "official" USYD colours and guides, from [USYD brand guidelines](https://intranet.sydney.edu.au/services/marketing-communications/our-brand.html).
|
https://github.com/Aariq/mycv | https://raw.githubusercontent.com/Aariq/mycv/main/_extensions/mycv/typst-show.typ | typst | #show: doc => cv(
$if(jobtitle)$
title: [$jobtitle$],
$endif$
$if(name)$
author: [$name$],
$endif$
$if(affiliation)$
affiliation: "$affiliation$",
$endif$
$if(phone)$
phone: [$phone$],
$endif$
$if(email)$
email: "$email$",
$endif$
$if(url)$
website: "$url$",
$endif$
$if(github)$
github: "$github$",
$endif$
$if(linkedin)$
linkedin: "$linkedin$",
$endif$
$if(font)$
font: "$font$",
$endif$
doc,
)
//function for formatting entries into columns
#let cvdateentry(..content) = {
grid(
columns: (0.15fr, 0.85fr),
row-gutter: 1.2em,
..content
)
}
#let pubentry(content, boldauth: none) ={
set par(hanging-indent: 10pt)
if boldauth == none {
content
} else {
show boldauth: str => [*#str*]
content
}
} |
|
https://github.com/viniciusmuller/ex_typst | https://raw.githubusercontent.com/viniciusmuller/ex_typst/main/native/extypst_nif/README.md | markdown | Apache License 2.0 | # NIF for Elixir.ExTypst.NIF
## To build the NIF module:
- Your NIF will now build along with your project.
## To load the NIF:
```elixir
defmodule ExTypst.NIF do
use Rustler, otp_app: :ex_typst, crate: "extypst_nif"
# When your NIF is loaded, it will override this function.
def add(_a, _b), do: :erlang.nif_error(:nif_not_loaded)
end
```
## Examples
[This](https://github.com/rusterlium/NifIo) is a complete example of a NIF written in Rust.
|
https://github.com/tingerrr/typst-test | https://raw.githubusercontent.com/tingerrr/typst-test/main/docs/book/src/README.md | markdown | MIT License | # Introduction
`typst-test` is a test runner for [Typst](https://typst.app/) projects. It helps you worry less about regressions and speeds up your development.
<script src="https://asciinema.org/a/669405.js" id="asciicast-669405" async="true"></script>
## Bird's-Eye View
Out of the box `typst-test` supports the following features:
- locate the project it is invoked in
- collect and manage test scripts and references
- compile and run tests
- compare test output to references
- provide extra scripting functionality
- running custom scripts for test automation
## A Closer Look
This book contains a few sections aimed at answering the most common questions right out the gate.
- [Installation](./quickstart/install.md) outlines various ways to install `typst-test`.
- [Usage](./quickstart/usage.md) goes over some basic commands to get started with `typst-test`.
After the quick start, a few guides delve deeper into some advanced topics.
- [Writing Tests](./guides/tests.md) inspects adding, removing, updating and editing tests more closely.
- [Using Test Sets](./guides/test-sets.md) delves into the test set language and how it can be used to isolate tests and speed up your TDD workflow.
- [Automation](./guides/automation.md) explains the ins and outs of hooks and how they can be used for testing typst preprocessors or formatters.
- [Setting Up CI](./guides/ci.md) shows how to set up `typst-test` to continuously test all changes to your package.
The later sections of the book are a technical reference to `typst-test` and its various features or concepts.
- [Tests](./reference/tests/index.md) outlines which types of tests `typst-test` supports, how they can be customized and which features are offered within the test scripts.
- [Test Set Language](./reference/test-sets/index.md) defines the test set language and its built in test sets.
- [Configuration Schema](./reference/config.md) lists all existing config options, their expected types and default values.
- [Command Line Tool](./reference/cli/index.md) goes over `typst-test`s various sub commands, arguments and options.
|
https://github.com/jultty/hello-typst | https://raw.githubusercontent.com/jultty/hello-typst/main/README.md | markdown | # hello typst
A study into [typst](https://typst.app/), a typesetting system able to create PDF files programmatically.
|
|
https://github.com/matetamasi/Medve-Automata-9 | https://raw.githubusercontent.com/matetamasi/Medve-Automata-9/master/merchant.typ | typst | #let fickle = [
== Without a hat
If they ask for an *apple*,\
give them an apple and put on your hat.\
If they ask for a *banana*,\
give them a banana.
== With a hat
If they ask for an *apple*,\
give them a banana and take off your hat.\
If they ask for a *banana*,\
give them an apple.
]
#let frustrating = [
== Without a hat
If they ask for an *apple*,\
give them an apple and put on your hat.\
If they ask for a *banana*,\
give them a banana.
== With a hat
If they ask for an *apple*,\
give them a banana and take off your hat.\
If they ask for a *banana*,
give them a banana.
]
#let fancy = [
== Without a hat, sitting
If they ask for an *apple*,\
give them an apple and put on your hat.\
If they ask for a *banana*,\
give them a banana and stand up.
== With a hat, sitting
If they ask for an *apple*,\
give them an apple and stand up.\
If they ask for a *banana*,\
give them an apple.
== Without a hat, standing
If they ask for an *apple*,\
give them a banana and sit down.\
If they ask for a *banana*,\
give them a banana.
== With a hat, standing
If they ask for an *apple*,\
give them an apple and sit down.\
If they ask for a *banana*,\
give them a banana and take off your hat.
]
#table( columns: 3,
[#fickle],
[#fickle],
[#fickle],
[#fickle],
[#fickle],
[#fickle],
[#fickle],
[#fickle],
[#fickle],
)
#pagebreak()
#table(columns: 3,
[#frustrating],
[#frustrating],
[#frustrating],
[#frustrating],
[#frustrating],
[#frustrating],
[#frustrating],
[#frustrating],
[#frustrating],
)
#pagebreak()
#table(columns: 3,
[#fancy],
[#fancy],
[#fancy],
)
#pagebreak()
#table(columns: 3,
[#figure(image("./alma.jpg"))],
[#figure(image("./alma.jpg"))],
[#figure(image("./alma.jpg"))],
[#figure(image("./alma.jpg"))],
[#figure(image("./alma.jpg"))],
[#figure(image("./alma.jpg"))],
[#figure(image("./alma.jpg"))],
[#figure(image("./alma.jpg"))],
[#figure(image("./alma.jpg"))],
)
#table(columns: 2,
[#figure(image("./banan.jpg"))],
[#figure(image("./banan.jpg"))],
[#figure(image("./banan.jpg"))],
[#figure(image("./banan.jpg"))],
[#figure(image("./banan.jpg"))],
[#figure(image("./banan.jpg"))],
[#figure(image("./banan.jpg"))],
[#figure(image("./banan.jpg"))],
[#figure(image("./banan.jpg"))],
[#figure(image("./banan.jpg"))],
[#figure(image("./banan.jpg"))],
[#figure(image("./banan.jpg"))],
)
|
|
https://github.com/Myriad-Dreamin/tinymist | https://raw.githubusercontent.com/Myriad-Dreamin/tinymist/main/syntaxes/textmate/tests/unit/basic/space-control-flow.typ | typst | Apache License 2.0 | #let A = []
#for i in range(0, 10) { A } { A }
#for i in { range(0, 10) } { A } { A }
#if { true } { A } { A }
#for i in range(0, 10){A}{A}
#for i in { range(0, 10) }{A}{A}
#if{true}{A}{A}
#for i in range(0, 10) { A }A
#for i in { range(0, 10) } { A }A
#if { true } { A }A
#for i in range(0, 10){A}A
#for i in { range(0, 10) }{A}A
#if{true}{A}A
|
https://github.com/goshakowska/Typstdiff | https://raw.githubusercontent.com/goshakowska/Typstdiff/main/tests/test_complex/ordered_list/ordered_list_inserted.typ | typst | + The climate intensive
- Precipitation important
- Temperature scales
+ degree
- hot
- cold
- warm
- really hot
+ sun
+ cloud
+ wind
+ The geology
+ something new |
|
https://github.com/AxiomOfChoices/Typst | https://raw.githubusercontent.com/AxiomOfChoices/Typst/master/Courses/Math%20591%20-%20Mathematical%20Logic/Assignments/Assignment%204.typ | typst | #import "/Templates/generic.typ": latex, header
#import "@preview/ctheorems:1.1.0": *
#import "/Templates/math.typ": *
#import "/Templates/assignment.typ": *
#import "@preview/cetz:0.2.0"
#let head(doc) = header(doc, title: "Assignment 4")
#show: head
#show: latex
#show: NumberingAfter
#show: thmrules
#show: symbol_replacing
#set page(margin: (x: 1.6cm, top: 2.5cm, bottom: 1.9cm))
#show math.equation: it => {
if it.has("label"){
return math.equation(block: true, numbering: "(1)", it)
}
else {
it
}
}
#show ref: it => {
let el = it.element
if el != none and el.func() == math.equation {
link(el.location(),numbering(
"(1)",
counter(math.equation).at(el.location()).at(0)+1
))
} else {
it
}
}
#let lemma = lemma.with(numbering: none)
#set enum(numbering: "(a)")
= Question
<question-1>
== Statement
Suppose $mM$ is an $aleph_0$-categorical structure. Show that a subset $A seq mM^n$ is invariant under the action of $Aut(mM)$ on $mM^n$ if and only if it is definable over $nothing$
== Solution
First assume that a subset is definable, that is
$
A = {ov(a) in mM^n : phi(ov(a))}
$
for some logical formula $phi$. Then we have for any $f in Aut(mM)$, since it is an isomorphism
$
phi(x) <=> phi(f(x))
$
and so
$
x in A <=> f(x) in A
$
hence $A$ is invariant.
#claim[
The orbits of $mM^n$ under the action of $Aut(mM)$ are $p(mM)$ for complete types $p in S_n^Th(mM) (nothing)$.
]
#proof[
Clearly $p(mM)$ is invariant under the action of $Aut(mM)$, now let $ov(a),ov(b)$ be two tuples of the same type. We have a partial isomorphism $f: ov(a) -> ov(b)$, we now will use back and forth to construct this to an automorphism. By induction we assume $A_n$ and $B_n$ have the same type, then assume we want to add $a$ to $A_n$, then $tp^mM (A_n, a)$ is a complete type.
Since $mM$ is $aleph_0$-categorical all its types are isolated and so $tp^mM (A_n, a)$ by a formula $phi(ov(x), y)$. Now the formula $exists y phi(ov(x),y)$ is a formula over $A_n$ which is in $tp^mM (A_n)$ and so is also in $tp^mM (B_n)$. We call $b$ the witness of this formula over $B_n$ and map $a$ to $b$ to extend the map.
This is the construction for odd steps, for even steps we just switch $A_n$ and $B_n$. The union of these partial isomorphism is then an isomorphism $mM -> mM$ that maps $ov(a)$ to $ov(b)$.
]
Now a set is invariant if and only if it is a union of orbits, and a set is definable if and only if it is a union of complete types. Since orbits are exactly compete types then we are done.
#pagebreak(weak: true)
= Question
== Statement
Let $alpha < omega_1$ be an ordinal and let $mM$ and $mN$ be countable structures. Show that if $mM$ and $mN$ satisfy the same $cal(L)_(omega_1, omega)$-sentences of quantifier depth less or equal to $omega+alpha$, then $mM equiv_alpha mN$. Show also that if $mM equiv_alpha mN$, then $mM$ and $mN$ satisfy the same $cal(L)_(omega_1, omega)$-sentences of quantifier depth at most $alpha$.
== Solution
#claim[
The sentences $phi^(mM)_(alpha)$ we saw in class have quantifier depth at most $omega+alpha$.
]
#proof[
We prove by induction. We clearly see that
$
phi_0^mM = and.big_(phi in Th(mM)) phi
$
and so since these are sentences all have finite quantifier depth we get that $qd(phi_0^mM) <= omega$.
In the limit we have
$
phi_alpha^mM = and.big_(beta < alpha) phi_(beta)^mM
$
and so we have $qd(phi_alpha^mM) = sup(qd(phi_beta^mM)) <= sup(omega + beta) = omega + alpha$.
In the successor step we have
$
phi_(alpha+1)^mM =
(and.big_(b in mM) exists y phi_alpha^(mM, b) (y))
and
(forall y or.big_(b in mM) phi_alpha^(mM, b) (y)).
$
and so
$
qd(phi_(alpha+1)^mM)
&=
max(sup(qd(phi_alpha^(mM, b)) + 1), sup(qd(phi_alpha^(mM,b) + 1)))
\ &=
sup(qd(phi_alpha^(mM, b)) + 1)
<=
omega + alpha + 1
$
]
So if $mM$ and $mN$ agree on all $cal(L)_(omega_1,omega)$ sentences of quantifier depth at most $omega+alpha$ then they agree on $phi_alpha^mM$ and thus from class we know that $mM equiv_alpha mN$.
On the other hand assume that $mM equiv_alpha mN$, then we prove by induction on the structure of sentences that they satisfy the same $cal(L)_(omega_1,omega)$-sentences of quantifier depth at most $alpha$.
For standard sentences without infinite-ary logic this is trivial since $mM equiv_0 mN$ implies they have the same theory.
If $phi = not psi$ for some $psi$ of quantifier depth at most $alpha$, then by induction
$
mM sat psi <=> mN sat psi "implies" mM sat phi <=> mN sat phi
$
and so the statement follows.
If $phi = exists x (psi(x))$ for some $psi$, then $alpha = beta + 1$ where $psi$ is of quantifier depth at most $beta$. Then assume $phi$ holds in one model, say $mM$, then for some $a in mM$ we have that $mM sat psi(a)$. But now since $mM equiv_(alpha) mN$ then for some $b in mN$ we have $(mM, a) equiv_(beta) (mN, b)$ so by inductive hypothesis we have that $mN sat psi(b)$ so $mN sat phi$. The same proof works for the other direction.
Finally if $phi = and.big_(alpha) psi_alpha$ for $psi_alpha$ of quantifier depth at most $alpha$, then by inductive hypothesis
$
mM sat psi_alpha <=> mN sat psi_alpha
$
and so since this is true for all $alpha$ it also holds for their conjunction and thus for $phi$.
#pagebreak(weak: true)
= Question
== Statement
Let $mM$ and $mN$ be countable structures and of the same Scott rank $alpha$.
Show that if $mN equiv_(alpha+omega) mM$, then $mN$ is isomorphic $mM$.
== Solution
We construct the isomorphism by back and forth, by induction we will construct maps $f_n : A_n -> B_n$ such that $(mM, A_n) equiv_(alpha+1) (mN, B_n)$. For the base case this is trivial, so assume for the induction step that we have the map $f_n$.
Now we want to add a specific element $a in mM$ to $A_n$, so by definition of $equiv_(alpha+1)$ there is some element $b in mN$ such that $(mM, A_n, a) equiv_(alpha) (mN, B_n, b)$. Now we also know that $mM equiv_(alpha + n + 2) mN$ so again by definition we can pick elements $c_i in mN$ such that, if we define $C_n = { c_i : i <= n }$ then we have
$
(mM, A_n, a) equiv_(alpha+1) (mN, C_n, c_(n+1)).
$
Now notice that
$
(mN, B_n, b) equiv_(alpha) (mM, A_n, a) equiv_alpha (mN, C_n, c_(n+1)),
$
so we have that $(mN, B_n, b) equiv_alpha (mN, C_n, c_(n+1))$.
But since the Scott rank of $mN$ is $alpha$ then that also means that $(mN, B_n, b) equiv_(alpha+1) (mN, C_n, c_(n+1))$.
We thus have
$
(mN, B_n, b) equiv_(alpha+1) (mN, C_n, c_(n+1)) equiv_(alpha+1) (mM, A_n, a)
$
so $(mN, B_n, b) equiv_(alpha+1) (mM, A_n, a)$ which completes the proof.
#pagebreak(weak: true)
= Question
== Statement
Show that the theory of atomless Boolean algebras has quantifier elimination.
== Solution
In assignment 3 we showed that the complete types of this theory are all isolated by the finite orders within said types. But the finite orders that isolate them are quantifier free formulas so all the complete types are isolated by quantifier free formulas. Since this is true from class we know that this theory has quantifier elimination.
#pagebreak(weak: true)
= Question
== Statement
Does every $aleph_0$-categorical theory has quantifier elimination?
== Solution
The answer is no, to see this consider the theory of dense linear orders with end points, a model of which is for example $QQ sect [0,1]$. This theory is $aleph_0$-categorical since you can construct the isomorphism by just removing the endpoints, using $aleph_0$-categoricity of dense linear orders without endpoints and then just mapping the endpoints to each other.
This theory does not have quantifier elimination, to see this simply note that this is a relational language, so all quantifier free formulas in one variable are logically equivalent to true or false. However, we have 3 different types over one element in this theory, one is the type of the interior, which is isolated by
$
phi(x) = exists y (y > x) and exists y (y < x)
$
one is the type of the top endpoint which is isolated by
$
phi(x) = forall y (not (y > x))
$
and the last one is the one of the bottom endpoint, which is isolated by
$
phi(x) = forall y (not (y < x))
$
|
|
https://github.com/rxt1077/it610 | https://raw.githubusercontent.com/rxt1077/it610/master/markup/slides/missing.typ | typst | #import "/templates/slides.typ": *
//#import "@preview/fletcher:0.5.1" as fletcher: diagram, node, edge
#import "/typst-fletcher/src/exports.typ" as fletcher: diagram, node, edge
#show: university-theme.with(short-title: [Missing])
#title-slide(title: [What's missing?])
#focus-slide()[
We've been learning in a virtualized environment.
What haven't we had a chance to work with?
]
#let blob(pos, label, tint: white, ..args) = node(
pos, align(center, label),
fill: tint.lighten(60%),
stroke: 1pt + tint.darken(20%),
shape: rect,
corner-radius: 5pt,
..args,
)
#slide(title: [The Boot Process])[
#align(
center + horizon,
diagram(
blob((0,0), [
BIOS \
\
configuration \
POST
], tint: red),
edge("-|>"),
blob((1, 0), [
Bootloader \
\
GRUB, LILO, \
SYSLINUX, PXE
], tint: orange),
edge("-|>"),
blob((2, 0), [
Kernel \
\
via boot partition \
or possibly network
], tint: yellow),
edge((2, 0), (2, 0.5), (0, 0.5), (0, 1), "-|>"),
blob((0, 1), [
init \
\
systemd, runit, \
SysVinit, upstart
], tint: green),
edge("-|>"),
blob((1, 1), [
init scripts \
\
init system \
dependent
], tint: blue),
edge("-|>"),
blob((2, 1), [
daemons \
\
services, etc.
], tint: purple),
)
)
]
#alternate(
title: [Init System],
image: licensed-image(
file: "/images/number-one.jpg",
license: "CC BY-NC-ND 2.0",
title: [Foam Finger Fun!],
url: "https://www.flickr.com/photos/pecma/9449255933",
author: [<NAME>],
author-url: "https://www.flickr.com/photos/pecma/",
),
text: [
- PID 1
- SysV was the old way of doing it
- Most modern systems run sytemd (it's conentious)
- The init system brings up and monitors daemon processes
],
)
#alternate(
title: [Basic systemctl Commands],
image: licensed-image(
file: "/images/systemd-light.svg",
license: "CC BY-SA 4.0",
title: [Full Color Logo],
url: "https://brand.systemd.io/",
author: [<NAME>],
author-url: "https://tobiasbernard.com/",
),
text: text(size: 20pt)[
- `systemctl list-units --type=service`
- `systemctl start <servicename>`
- `systemctl stop <servicename>`
- `systemctl restart <servicename>`
- `systemctl enable <servicename>`
],
)
#alternate(
title: [Processes],
image: image("/images/ps.png"),
text: [
- OS kernel allows for multiple things to run at once
- A process is one of those things
- The kernel scheduler splits time between them
- #link("https://documentation.suse.com/sles/15-SP1/html/SLES-all/cha-tuning-taskscheduler.html")[This can be adjusted!]
]
)
#alternate(
title: [Tuning the Process Scheduler],
image: {
set text(size: 0.75em)
let R = (1, 1)
let D = (0, 0)
let S = (0, 2)
let T = (2, 0)
let Z = (2, 2)
diagram(
spacing: 1em,
label-sep: 0em,
label-size: 0.8em,
blob(R, [
Running \
Runnable \
(R)
], tint: green),
blob(D, [
Uninterruptible \
Sleep \
(D)
], tint: blue),
blob(S, [
Interruptible \
Sleep \
(S)
], tint: blue),
blob(T, [
Stopped \
(T)
], tint: yellow),
blob(Z, [
Zombie \
(Z)
], tint: red),
edge(R, D, "-|>", bend: -20deg),
edge(D, R, "-|>", [wake up], bend: -20deg, label-angle: auto),
edge(R, S, "-|>", bend: -20deg),
edge(S, R, "-|>", [
wake up \
signal
], bend: -20deg, label-angle: auto),
edge(R, T, "-|>", [SIGSTOP], bend: -20deg, label-angle: auto),
edge(T, R, "-|>", [SIGCONT], bend: -20deg, label-angle: auto),
edge(R, Z, "-|>", [exit()], label-side: left, bend: -20deg, label-angle: auto),
)
},
text: [
- `/proc/sched_debug` shows all tunable variables
- `sysctl` (not systemctl!) can be used to adjust them
- `chrt` shows the real-time attributes of a running process
- If you make changes, don't forget to make them permanent! (/etc/sysctl.conf)
]
)
#alternate(
title: [Devices],
image: [
#set text(size: 10pt)
#grid(
columns: (1fr),
rows: (20%, 60%, 20%),
grid.cell(
fill: green.lighten(80%),
box(
inset: 8pt,
grid(
columns: (1fr, 1fr, 1fr, 1fr, 1fr, 1fr),
rows: (1em, 1fr),
gutter: 10pt,
align: center + horizon,
fill: green.lighten(20%),
grid.cell(fill: none, colspan: 6, [User Space]),
[bash],
[neovim],
[wayland],
[ssh],
[python],
[firefox],
)
)
),
grid.cell(
fill: yellow.lighten(80%),
box(
inset: 8pt,
grid(
columns: (1fr, 1fr, 1fr, 1fr, 1fr),
rows: (1em, 1fr, 1fr, 1fr, 1fr),
gutter: 8pt,
align: center + horizon,
fill: yellow.lighten(20%),
grid.cell(fill: none, colspan: 5, [Kernel Space]),
grid.cell(rowspan: 4, [Process Management and Architecture Dependent Code]),
grid.cell(rowspan: 4, [Memory Management for Physical and Virtual Memories]),
grid.cell(rowspan: 2, [Network Stack / Subsystem]),
grid.cell(colspan: 2, [Virtual File System]),
[File System Drivers],
grid.cell(rowspan: 2, [Character Drivers and Friends]),
[Network Device Drivers],
[Block Device Drivers],
grid.cell(colspan: 3, [Hardware Protocol Layers (PCI, USB, I#super[2]C...)]),
),
),
),
grid.cell(
fill: red.lighten(80%),
box(
inset: 8pt,
grid(
columns: (1fr, 1fr, 1fr, 1fr, 1fr),
rows: (1em, 1fr),
gutter: 8pt,
align: center + horizon,
fill: red.lighten(20%),
grid.cell(fill: none, colspan: 5, [Hardware Space]),
[CPU],
[Memory],
[Network Interfaces],
[Storage Devices],
[All Other Devices],
),
),
),
)
],
text: [
- Real systems have real devices
- I/O is a typical bottleneck in production systems
- #link("https://cromwell-intl.com/open-source/performance-tuning/disks.html")[Sysfs allows for tuning of I/O devices]
- I/O also has schedulers
],
)
#slide(title: [udev])[
#v(1fr)
- A list of rules that determines what to do/create when a device is added
- Devices can have persistent names through devfs (can be very useful for USB)
- Initialization can take place automatically
#code(title: [/lib/udev/rules.d/80-usb.rules])[
```udev
KERNEL=="sd*", SUBSYSTEMS=="scsi", ATTRS{model}=="USB 2.0 Storage Device", SYMLINK+="usbhd%n"
```
]
#v(1fr)
]
#alternate(
title: [General Advice for Tuning Linux],
image: licensed-image(
file: "/images/advice-icon.svg",
license: "UXWING",
title: [Advice Icon],
url: "https://uxwing.com/advice-icon/",
),
text: [
- Determine your metric in advance!
- Take slow steps and monitor changes
- Be prepared to walk-back changes
],
)
|
|
https://github.com/minijackson/2024-04-hepix-nix | https://raw.githubusercontent.com/minijackson/2024-04-hepix-nix/master/theme.typ | typst | #import "@preview/polylux:0.3.1": *
#let colors = (
red: rgb("E50019"),
blue: rgb("3E4A83"),
lightBlue: rgb("7E9CBB"),
gray: rgb("262626"),
yellow: rgb("FFCD31"),
archipel: rgb("00939d"),
macaron: rgb("da837b"),
opera: rgb("bd987a"),
glycine: rgb("a72587"),
)
#let backdrop(dx: relative, dy: relative) = align(
top + right,
move(
dx: dx,
dy: dy,
image("frame-backdrop.svg", height: 200pt)
)
)
#let cea-theme(
aspect-ratio: "16-9",
body,
) = {
set text(size: 21pt, font: "Libertinus Serif")
show raw: set text(font: "Fira Code")
set page(
header: backdrop(dx: 232pt, dy: -73pt),
header-ascent: 100%,
paper: "presentation-" + aspect-ratio,
margin: (x: 2em, top: 1.5em, bottom: 2.5em),
)
show heading.where(level: 1): set heading(numbering: "1.")
show heading.where(level: 2): set text(fill: colors.red)
show heading: it => block(inset: (bottom: 1em))[#it]
body
}
#let title-slide(title: [], author: none, subtitle: none) = {
show heading.where(level: 1): set heading(numbering: none)
logic.polylux-slide({
align(top + left, image("IRFU.svg", height: 125pt))
heading(level: 1, title)
if author != none {
par(author)
}
if subtitle != none {
par(subtitle)
}
})
}
#let slide(body) = {
set page(
header: backdrop(dx: 170pt, dy: -153pt),
footer: {
set text(size: 10pt, fill: luma(100))
box(
height: 3em,
grid(
columns: (5em, 1fr, 2fr, 5em),
align(left + horizon, image("CEA.svg")),
align(center + horizon, "CEA/DRF/IRFU/DIS/LDISC"),
align(center + horizon, "HEPiX Spring 2024"),
align(center + horizon, logic.logical-slide.display() + "/" + context { logic.logical-slide.final().at(0) }),
)
)
},
)
logic.polylux-slide(body)
}
#let section-slide(background: colors.blue, foreground: white, body) = {
show heading: it => {
set text(fill: foreground, size: 2.5em)
if it.numbering != none {
text(size: 2em, counter(heading).display(it.numbering))
[~]
}
it.body
}
set page(
fill: background,
margin: 2em,
footer: [],
header: {
block(
height: 50pt,
move(
dx: -2em - 2pt,
dy: 54pt,
image("section-backdrop.svg", width: 100% + 4em + 27pt, height: 95pt)
)
)
},
header-ascent: 100%,
)
set text(fill: foreground)
let content = { v(.1fr); body; v(.1fr) }
logic.polylux-slide(align(horizon, body))
}
// vim: filetype=typst
|
|
https://github.com/soarowl20240613/geelypaper | https://raw.githubusercontent.com/soarowl20240613/geelypaper/main/paper_demo.typ | typst | #import "paper.typ": *
#let cnabstract = [随着科学技术的迅速发展,导致农村劳动力过剩,大部分人流入城市寻求生计,最终成为城市人口。这就使得城市人口流动增加,房屋租赁也成为人们关心的重中之重。目前已有的房屋租赁方式有中介和小区物业进行代挂,但是这种传统的人为管理的方式存在很多弊端。比如说房源的真假难以分辨,看房过程繁琐,甚至还存在很多中介跑路的情况。当然市面上也有一部分看房软件,但经过调查出现很多监管不到位,房源虚假,中介费高和房源少等问题 @barb。
所以,笔者做了一款房屋租赁系统来试图解决人们看房的困难。一款房屋租赁系统的存在可以带来很多好处。首先,它可以让房东和租户更容易地连接起来,节省彼此的时间和精力。其次,系统可以提供一些自动化功能,如在线预订、租金支付和合同签署等,使整个租赁过程更加快捷方便。此外,系统还可以提供租户信用评分、房源信息管理等功能,有助于提高租赁市场的透明度和规范性。最后,对于平台运营商而言,这类系统也是创造盈利模式的一个途径,因为他们可以通过收取服务费或广告费等方式获得收入 @camb。
该系统采用前后端分离的设计理念,前端主要采用Vue框架。当前Vue是Javascript使用最常用的框架,因为Vue可用性高,并且用法多、范围广、对界面饱满有很大作用;后端部分使用SpringBoot框架,SpringBoot框架更加高效安全可靠,解决了配置复杂冗余的问题,而且还具有很多非功能特性,是作为计算机本科生必须掌握的技术;后台数据使用MySQL进行管理。]
#let enabstract = [With the rapid development of science and technology, there is a surplus of labor force in rural areas. Most of them flow into cities to seek livelihoods and eventually become urban population. This makes urban population mobility increase, housing rental has become the top priority of people's concern. At present, there are existing ways of housing rental agents and residential properties, but this traditional way of artificial management has many drawbacks. For example, the real estate is difficult to distinguish between the real estate and the real estate, and there are even many intermediaries running away. Of course, there are some house-viewing software on the market, but after investigation, there are many problems such as inadequate supervision, false housing, high agency fees and few housing resources @donne.
So, I built a rental system to try to solve the problem of people looking at houses. The existence of a rental system can bring many benefits. First, it allows landlords and tenants to connect more easily, saving each other time and effort. Secondly, the system can provide some automatic functions, such as online booking, rent payment and contract signing, to make the whole leasing process faster and more convenient. In addition, the system can also provide tenants with credit scores, housing information management and other functions, helping to improve the transparency and standardization of the rental market. Finally, for platform operators, such systems are also a way to create a revenue model, as they can earn revenue by charging for services or advertising.
The system adopts the design concept of separating the front and rear ends, and the front end mainly uses the Vue framework. At present, Vue is the most commonly used framework for Javascript, because Vue has high availability, and a wide range of usage, full interface has a great role; The back-end part uses SpringBoot framework, which is more efficient, safe and reliable, solves the problem of complex and redundant configuration, and also has many non-functional features, which is a technology that must be mastered by computer undergraduates. Backend data is managed using MySQL.]
#show: paper.with(
title: "房屋租赁管理系统设计与实现",
faculty: "智能科技学院",
class: "2021级计算机科学与技术(专升本)3班",
author: "袁天罡",
studentnumber: "211124010635",
adviser: "卓能文",
date: "二〇二四年五月",
cnabstract: cnabstract,
cnkeywords: ("Vue", "SpringBoot框架", "MySQL", "交互"),
enabstract: enabstract,
enkeywords: ("Vue", "SpringBoot framework", "MySQL", "interaction"),
)
= 绪论
== 研究目的和意义
本课题计划完成一个全面可靠高效能实现信息透明化的房屋租赁管理系统 @drill。通过完成并完善本选题,总结了本科学期期间的知识点,充分培养了动手能力,学以致用实践代码的编写。并且在解决问题的过程中,对Java技术有进一步的认知,提高自己的综合水平,锻炼今后的工作中遇到困难的解决钻研能力。
房屋租赁系统是一个在线平台,用于连接房东和租户,并提供一些自动化功能,使整个租赁过程更加便捷。它的出现可以带来多方面的意义,下面笔者将详细阐述。
首先,房屋租赁系统可以促进市场的透明度和规范性。在传统的租赁市场中,信息不对称、合同不规范等问题比较普遍 @foia,这给租户和房东都带来了很多麻烦。而房屋租赁系统能够提供租户信用评分、房源信息管理等功能,让市场更加清晰透明。租户可以更加直观地评估房东和房源的可靠程度,从而做出更加明智的决策。房东也可以通过系统进行精准定价、优化房屋配置、提高竞争力,从而获得更好的租客来源和租金收益。
其次,房屋租赁系统可以提高租赁效率和用户体验。通过在线预订、租金支付、合同签署等自动化流程,租户和房东可以省去很多繁琐的手续和沟通过程,节约时间和精力。在租赁过程中,系统还可以提供在线客服、售后服务等功能,让用户获得更好的使用体验和感受。
第三,房屋租赁系统可以促进科技创新和数字化转型。随着信息技术的不断发展,越来越多的企业开始将传统业务与互联网结合,尝试探索新的商业模式。房屋租赁系统作为一种典型的互联网+业态,正是应用了信息技术和数字化手段,使得租赁市场变得更加智能、高效、便捷。同时,系统的开发和运营也需要涉及多种技术和人才,有助于提升整个行业的科技含量和创新能力。
最后,对于平台运营商而言,房屋租赁系统也是创造盈利模式的一个途径。通过收取服务费或广告费等方式获得收入,并通过数据分析和挖掘等手段获取更多商业机会,这些都是房屋租赁系统带来的商业价值。
总之,通过本课题的研究,目的是针对存在的房屋租赁问题进行改善,实现信息的公开透明化,全面收集数据解决房源少的问题。建立平台政策和优化监管功能,提高房屋租赁平台的综合水平,对人们的生活带来便利。
== 研究背景
=== 国内发展(应用)现状
目前国内的城镇化战略使得人口重心移动,流入城市人口过多,城市建设发展加快。由于这些因素房价增长,房租租赁建设紧张,越来越多的房屋租赁软件崛起,但是也存在着巨大缺陷。
首先是链家成立于2001年,是中国领先的房地产服务企业。业务覆盖广,房源质量高,服务者素质高。上面的房源基本上是通过中介上传来进行出租,虽然优点颇多,但是需要交过高的中介费,这对刚毕业的大学生和刚在城市工作的人不太友好。
随后2007年安居客挤入租房行列,独有的“个人房源”选项虽然采用真实照片,但是少之甚少,大部分还是中介上传并且很多房源还是虚假房源。据调查显示,安居客很多黑中介,会泄露用户个人信息,所以这是严重的监管不到位和信息不透明的现象。
通过对十年来租房平台弊端的总结以及改善,于2011年成立自如租房,也是链家产业下的长租公寓品牌。一改往日的中介入驻,使用自己的管家联系户主进行拍照看房,保障房源都是真实可靠的。但盈利模式是赚取差价以及收取服务费,价格往往高于市场价。
由此看来,国内的房屋租赁系统在不断创新、提升用户体验和服务质量方面已经取得了很大的进展。随着市场竞争的加剧和技术的迭代升级,这些平台也将会带来更多的变化和发展。
=== 国外发展(应用)现状
国外的房屋租赁系统发展状况相对较为成熟已经形成了一些领先的平台和商业模式。下面举几个典型的例子。
Zillow是一个美国的房地产信息网站,提供买卖房屋、出租房屋、房屋估价和市场分析等服务。它将各种房源信息整合到一起,在线显示给用户,方便他们进行筛选和比较。同时,它还提供比较精准的房屋估价功能,帮助房东和买家得到更好的交易结果。Zillow目前已经成为美国房地产市场上的重要参与者之一。
Rightmove创建于2000年是英国本地最大的房地产网站。房源多,信息量庞大并且还有很多自定义选项,比如说带不带家具,预算价格和选择区域。缺点是房租坐地起价。价格经常随市场变动,房源多虚拟信息也多不方便管理。
apartment.com也创建于2000年。是美国目前功能完善,房源信息真实,操作方便快捷的房屋租赁网站。优点在于非常定制化满足租客需求,功能全面选择也多,房东友善与租客和睦共处。但需要走很多流程,也需要一些良好信用要求,只适合一些稳定的租客。
总之,国外的房屋租赁系统在创新商业模式、提升用户体验、拓展市场规模等方面都取得了很大的成就。未来随着技术的不断进步和市场的不断竞争,这些平台将继续探索新的发展机遇和商业模式,并为全球的租赁市场带来更多创新和变革。
== 论文结构
本文的内容主要包括以下八个部分:
第一部分是绪论,分别从国内和国外两个方面对房屋租赁管理系统设计与实现进行了背景介绍,主要说明了这次对房屋租赁管理系统开发的主要原因。
第二部分是对房屋租赁管理系统过程中需要用到的预备知识、概念原理和技术进行解释说明,在正式进行开发前需要对这些相关的理论进行系统地学习,以便理解开发过程。
第三部分是房屋租赁管理系统的用户权限设计,先对租客权限分析,然后对户主的权限分析以及对管理员权限的分析。
第四部分是对房屋租赁管理系统的整体设计,房屋租赁管理系统分为两个部分,前端设计模式和后端设计模式。
第五部分是系统的功能实现,首先对系统开发环境作了介绍,然后进行核心功能的实现。
第六部分是测试与优化,对游戏的运行效率进行了评估。
第七部分是总结篇,对该游戏进行了综述性的评述,并阐述了当前的不足以及将来可以进一步完善的地方。
最后列出了本文所参考的相关资料。
= 预备知识及原理说明
== MVP设计模式
MVP(Model-View-Presenter),是一种被广泛用于开发的架构设计模式,是由MVC延伸出来的衍生物。作为衍生物,MVP在整体的设计思想上继承了MVC,其中M(Model)负责数据的处理,V(View)负责界面数据的可视化和用户交互,而C&P(Controller&Presenter)在大体上均负责逻辑的处理。
如 @fig:mvp 中MVP架构图所示,在MVP设计模式中,Model的具体任务为从数据库中获取数据,并对数据加以简单处理或传递转存;View的任务则是将经过处理的数据以合理的形式展现出来,并提供用户可操作的交互点,完成数据的可视化转换;而Presenter,即是自MVC演变的核心,Presenter主要负责将Model所获取传递的数据进行加工转换,随后交付View进行展现。在整个MVP设计模式中,Presenter作为Model与View的传递桥梁,在帮助两者沟通的同时,又隔绝了两者,即View无法直接跳过Presenter对Model进行操作。
#figure(
caption: [MVP架构图],
image("img/mvp.png", width: 50%),
) <mvp>
这样的分隔式处理,使Model和View达到完全分离,Model不受View的影响,降低了模块与模块间的耦合;同时这样的设计模式也简化了Activity的工作任务,在Activity中只需要处理生命周期的任务,使代码在一定程度上更加简洁明了;由于业务逻辑被分配至Presenter模块中,使得Activity不会因为后台线程的引用而无法回收资源,有效的避免了Activity的内存泄漏;模块间的联系紧密程度降低,且各模块有各自明确的分工,这使得代码的层次更加清晰,提高了代码的可读性;而Presenter多样的具体实现让单元测试变得更加便捷。
== 开发语言和开发工具
本次研究的开发语言主要使用Java。作为Android软件目前的主流开发语言,相较于C++更为简单,同时又摘取了许多其它开发语言的优点特性,而面向对象的编程是Java语言最主要的特点之一。作为被普遍使用的面向对象的编程语言的代表,Java不仅拥有所有面向对象编程语言都具备的普遍特性,即封装性、多态性以及继承性,它同时拥有动态联编性,更适应于面向对象的设计方法。除此之外,Java同时具有简单性、平台独立性、多线程以及安全可靠性的诸多优点。目前市面上的大多数Android软件都是运用Java语言进行开发,相对的,由于应用了Java核心类的知识,使得在安卓开发中Java语言占据了强有力的优势。
本次研究的开发工具使用Android Studio。Android Studio是由谷歌推出的一款Android集成开发工具,它基于IntelliJ IDEA,和Eclipse的安卓开发工具类似,为开发者提供了集成的Android开发工具。
== MySQL数据库
MySQL是一种关系型数据库管理系统(RDBMS),由瑞典MySQL AB公司开发,现在由Oracle公司拥有和维护。它是一款高效、可靠、稳定的开源数据库软件,是LAMP(Linux+Apache+MySQL+PHP)架构的重要组成部分,具有跨平台性和良好的兼容性。
MySQL支持多种操作系统(Linux、Windows、Mac OS等)以及多种编程语言(C、C++、Java、Python等),提供了完整的SQL标准,包括事务处理、触发器、存储过程、视图等功能。下面是MySQL的一些主要特点:
高性能: MySQL采用了多线程、异步I/O等技术,可以高效地处理大量数据请求。另外,MySQL还支持索引、查询优化等功能,可以提高数据的访问速度。
可靠性: MySQL支持数据备份、恢复等功能,可以保证数据的安全性和可靠性。此外,MySQL还支持主从复制、集群等功能,可以实现高可用性、容错性等特点。
易用性: MySQL的安装和配置比较简单,可以快速上手使用。同时,MySQL提供了完整的文档和社区支持,用户可以获取到丰富的资源和帮助。
开放性: MySQL是开源软件,可以免费使用和修改。同时,MySQL还拥有庞大的用户社区和开发者社区,可以实现定制化开发和二次开发等需求。
可扩展性: MySQL提供了完整的插件机制和API接口,可以方便地进行扩展和集成。开发者可以基于MySQL开发各种类型的应用程序,如电子商务、社交网络、游戏等。
总之,MySQL是一款成熟、稳定、可靠、高效、易用、开放和可扩展的关系型数据库管理系统。它被广泛应用于互联网领域,支撑着许多大型网站和应用程序的数据存储和处理,如Facebook、谷歌、雅虎、推特等。
== 版本控制软件Git
Git是一个开源的分布式版本控制工具,开发者们可使用GitHub等平台应用Git,进行协同开发。Git由Linus Torvalds开发,最初开发是为了满足团队Linus内核开发的需求,与常用的集中式版本控制工具不同,Git最大的特点就是采用了分布式的模式,摒弃了集中式工具中只有中心服务器的模式,每位参与开发的使用者都持有完整版本库,有效避免了使用集中式版本控制系统的协同开发中的不稳定性,不必担心中心服务器数据丢失,同时也加快了使用者们的代码交流。在Git的基本工作中主要分为四个版块,图中从左至右分别为:工作区间、暂存区、本地仓库以及远程仓库。其中,工作区间为工程目录文件,主要在工作区间执行Git命令;暂存区为暂存上传的代码数据的区间;本地仓库用来存储本地代码,同时是本地代码与远程代码的中转站;远程仓库为中心服务平台,用于远程保存提交的代码。Git基于这四个模块,构成了自身的基本工作流程:开发者修改工作区间的文件,执行add后文件将被添加到暂存区,随后commit提交会将文件保存至本地仓库,最终执行push推送,文件将会被传输到远程仓库进行保存。
== 本章小结
本章简要介绍了项目开发所需的相关知识,其中包括MVP设计模式的设计原理、所用的主要开发工具以及开发语言、MySQL数据库以及版本控制器Git的简介。以上四个模块的储备知识将为后续项目开发提供可靠的理论支持,加强本次研究的可行性。
= 用户权限设计分析
== 租客权限设计分析
房屋租赁系统的租客权限设计是保证系统信息安全、租户合法权益及资金安全的重要环节。在设计时,需要考虑以下几个方面:
+ 注册及登录权限: 租客以注册用户身份使用房屋租赁系统,需要提供基本的个人信息并完成注册流程。用户通过登录账号和密码访问系统并进行操作,登录过程需要进行身份验证。
+ 查询与浏览权限:租客可以在系统中浏览已发布的房源信息,并通过搜索等方式查询符合自己需求的房屋信息,但不允许修改任何房源信息。
+ 预订和支付权限:租客可以选择心仪的房源并提交预订请求。在预订期间,租客可以更改预订细节(如租期、价格、入住时间等),但对于一些核心数据,例如房东联系方式,租客无法直接获得。当确认预订后,租客将通过平台支付租金押金等费用。
+ 评价与投诉权限:租客有权在租期结束后评价房东、房源的质量,并且有权在必要的情况下投诉相关问题。评价和投诉信息将成为其他租客或房东参考的重要依据,因此也需要对评价和投诉信息的真实性进行保护。
+ 退款与维权权限:当租客在租期内出现合同纠纷或房源质量问题等情况时,拥有退款和维权的权利。退款和维权流程需要在平台规范的程序下操作,并需要提供相关证据以支持判断。
+ 个人信息保护:租客的个人隐私信息是需要得到网站的严格保护的。房屋租赁系统要求租客提供的信息应该仅限于必要的身份验证、预订等操作所需的必需信息。同时,房屋租赁系统也应该采取各种措施来确保用户信息的保密性。
总之,租客权限设计应该涵盖注册、浏览、预订、支付、评价、投诉、退款、维权和个人信息保护等方面,以保证租户在使用房屋租赁系统时,能够安全、便捷地完成租赁交易,并保护其合法权益。同时,由于每个房屋租赁系统的需求和特点不同,具体的权限设计还需要根据实际情况进行灵活调整和优化。
== 户主权限分析
房屋租赁系统中,户主(即房东)权限设计是保障系统信息安全、保护房东权益的关键环节。在设计时,需要考虑以下方面:
+ 房源发布与编辑权限:作为房东,他们可以在房屋租赁系统上发布自己的房源信息,并对信息进行修改、更新或删除。需要注意的是,为了保证租客的安全和信任,发布的信息需要经过平台的审核才能上线。
+ 订单管理权限:房东可以查看自己的订单列表,包括预订信息、租金支付情况、租客身份信息等,并且可以接受或拒绝预订请求。此外,房东还可以在租期结束后收到租客提供的评价和投诉信息。
+ 报表分析权限:为了了解自己的房产运营状况,房东应该具有数据分析及图表功能,以便更好地了解自己的房产出租状态。通过这个功能,房东可以查看订单、收支情况、退款等相关报表,从而获得及时的反馈和监控。
+ 合同签署权限:当租客确定预订房源之后,系统会生成一份标准的租赁合同,其中包括租期、租金、押金等重要信息。房东需要在签署合同前审查和确认租期等条款,确保自己的权益得到保障。
+ 费用管理权限:房东可以在系统中设定租金、押金以及其他费用,并查看租客的付款情况和账单结算。此外,当存在租客欠费或违约时,房东还可以使用平台提供的退款和维权流程进行相应操作。
+ 房源维护权限:房东需要保持房源的良好状态,包括维修、清洁、安全等方面。在出现问题时,房东可以通过平台提供的房屋维修服务来解决问题,保证租户的居住质量。
总之,房东权限设计需要涵盖房源发布、订单管理、报表分析、合同签署、费用管理和房源维护等方面,以保证房东能够方便、快捷地完成租赁交易,并保障房东的合法权益。同时,由于每个房屋租赁系统的需求和特点不同,具体的权限设计还需要根据实际情况进行灵活调整和优化。
== 管理员权限分析
房屋租赁系统的管理员权限设计是保证系统信息安全、维护平台稳定运营的重要环节。在设计时,需要考虑以下几个方面:
+ 用户管理权限:管理员需要管理所有注册用户的账号和个人信息。包括审查新用户注册申请、处理账号冻结、解锁等操作。
+ 房源管理权限:管理员需要审核并管理所有房东发布的房源信息,包括发布的内容、图片、价格、位置等信息的真实性和合规性。
+ 订单管理权限:管理员有权查看所有订单的状态、流程和相关信息,并对订单进行修改和删除。此外,管理员还能够协调和处理与订单相关的纠纷和退款问题。
+ 资金管理权限:管理员可以管理平台上所有的收支流水,包括租金支付、押金、提现等。应该对平台内的各种资金流通情况进行监控,及时发现和处理异常情况。
+ 系统维护权限:管理员有权查看平台的服务器负载、网站访问量等运营数据,以便根据实际情况优化系统。同时,管理员还需要确保系统的安全性,防范黑客攻击和信息泄露等安全事件。
+ 数据分析权限:管理员可以通过数据分析工具对平台内的各项指标进行分析和预测,以便更好地指导平台的运营策略。通过数据分析,管理员可以了解用户行为、市场趋势等信息,进而制定优化平台的策略。
总之,管理员权限设计需要涵盖用户管理、房源管理、订单管理、资金管理、系统维护和数据分析等多个方面,以保证管理员能够快速、高效地处理各种运营问题,并确保平台的稳定性和安全性。同时,由于每个房屋租赁系统的需求和特点不同,具体的权限设计还需要根据实际情况进行灵活调整和优化。
== 本章小结
本章主要通过绘制了项目的用例图和功能结构图,对用例分析、用例关系进行了较详细介绍。用户权限设计包含了三个部分,并对租客权限、户主权限以及管理员权限都做了并进行简要说明,完成了项目需求分析阶段的整体设计。
= 系统整体设计
== 前台设计
=== 概述
房屋租赁系统的管理员权限设计是保证系统信息安全、维护平台稳定运营的重要环节。在设计时,需要考虑以下几个方面:
用户管理权限:管理员需要管理所有注册用户的账号和个人信息。包括审查新用户注册申请、处理账号冻结、解锁等操作。
房源管理权限:管理员需要审核并管理所有房东发布的房源信息,包括发布的内容、图片、价格、位置等信息的真实性和合规性。
订单管理权限:管理员有权查看所有订单的状态、流程和相关信息,并对订单进行修改和删除。此外,管理员还能够协调和处理与订单相关的纠纷和退款问题。
资金管理权限:管理员可以管理平台上所有的收支流水,包括租金支付、押金、提现等。应该对平台内的各种资金流通情况进行监控,及时发现和处理异常情况。
系统维护权限:管理员有权查看平台的服务器负载、网站访问量等运营数据,以便根据实际情况优化系统。同时,管理员还需要确保系统的安全性,防范黑客攻击和信息泄露等安全事件。
数据分析权限:管理员可以通过数据分析工具对平台内的各项指标进行分析和预测,以便更好地指导平台的运营策略。通过数据分析,管理员可以了解用户行为、市场趋势等信息,进而制定优化平台的策略。
总之,管理员权限设计需要涵盖用户管理、房源管理、订单管理、资金管理、系统维护和数据分析等多个方面,以保证管理员能够快速、高效地处理各种运营问题,并确保平台的稳定性和安全性。同时,由于每个房屋租赁系统的需求和特点不同,具体的权限设计还需要根据实际情况进行灵活调整和优化。
=== 设计举例
==== 登录注册页面
在设计房屋租赁管理系统的登录注册功能时,需要考虑到用户体验、安全性和数据完整性等方面。以下是对登录注册页面的设想:
- 注册功能应该包括基本的个人信息,如用户名、密码、手机号码、邮箱等,并对用户输入信息的格式进行校验,确保其准确性。
- 登录功能可以使用用户名/手机号码/邮箱+密码的方式进行认证,也可以通过第三方登录(企业微信)来实现便捷登录。
- 为了保障用户的账号安全,应该设置密码强度要求,例如要求密码长度在6-16个字符之间,包含大小写字母、数字和特殊字符等。
- 对于忘记密码的情况,应该提供重置密码的功能,可以通过手机短信或邮箱验证来进行身份验证。
- 为了防止恶意注册和滥用系统资源,可以设置验证码功能,确保只有真实用户才能注册。
- 在用户注册成功后,可以通过邮件或短信的形式发送激活链接,确保用户账户的有效性。
- 在登录过程中可以使用JWT Token等技术来提高系统的安全性,避免明文传输密码等敏感信息。
- 为了方便用户管理自己的个人信息,可以在用户登录后提供个人中心页面,可供用户修改个人资料、查看订单等功能。
综上所述,登录注册是房屋租赁管理系统中的一个基础模块,合理设计并实现这个模块不仅可以提高用户体验,还能保障系统的安全性和数据完整性。
==== 增删改查
在设计房屋租赁管理系统的权限增删改查功能时,需要考虑到用户角色、权限类型、数据保护和操作审计等方面。以下是对增删改查的设想:
- 用户角色:在系统中需要对不同的用户进行角色分类,例如管理员、普通用户、房东等。每个用户角色都应该有对应的权限列表,限制其对系统中数据的访问和修改。
- 权限类型:在分配权限时,需要考虑到权限的粒度,例如可以为某个角色分配“查看房源”、“编辑房源”、“删除房源”等具体的权限。
- 数据保护:在设计权限控制功能时,需要考虑到对数据的访问控制,确保只有拥有合法权限的人员才能访问敏感数据。例如,在实现个人信息修改功能时,可以对用户密码/手机号等敏感信息进行加密处理,并通过访问控制策略管理数据访问权限。
- 操作审计:在系统中记录所有的权限操作,包括新增、删除和修改等,以便后续跟踪操作历史和查询问题根源。
在实现权限增删改查功能时,笔者们可以采用常用的RBAC(Role-Based Access Control)模型,该模型将权限授予给用户角色而非直接授予单个用户,可以有效地保证系统安全性和数据完整性。同时,可以使用框架中提供的权限管理模块来实现基础权限控制功能,例如Spring Security、Apache Shiro等。
综上所述,权限增删改查是房屋租赁管理系统中非常重要的一部分,需要合理设计并实现这个功能,以便保障用户数据的安全性和系统的稳定性。
== 后端设计
后端部分使用了Java的SpringBoot框架,并且采取的MySQL数据库来存储数据。在设计房屋租赁管理系统后端时,需要考虑到架构、技术栈、安全性和扩展性等方面。以下是一些设想部分:
- 架构:在确定系统架构时,可以采用分层架构或微服务架构,将业务逻辑、数据访问等功能进行分离并单独部署,提高系统的可维护性和扩展性。
- 技术栈:在选择技术栈时,可以考虑到开发效率、系统稳定性、性能和安全等方面,并选取相应的技术实现。在这次实现中将使用SpringBoot框架技术实现系统功能。
- 安全性:在保障系统安全性方面,可以采用多种措施,例如对用户输入的数据进行严格验证和过滤,使用SSL加密协议保证数据传输的安全,使用JWT Token等技术防止CSRF等攻击。
- 扩展性:在设计系统时,需要充分考虑到系统的可扩展性,使得系统能够满足未来的需求。例如,可以引入消息中间件,将不同的模块解耦,提高系统的可维护性和扩展性。
另外,在设计数据库时,需要考虑到数据表之间的关系,确保数据的完整性和一致性。例如,在房源表中可以添加房东ID字段,与房东信息表进行关联,便于查询、更新等操作。
综上所述,房屋租赁管理系统后端设计是非常重要的一部分,需要充分考虑到架构、技术栈、安全性和扩展性等方面,以实现系统的高可用性、高可扩展性和高性能。
== 后端开发可能使用的的关键类
在设计和开发房屋租赁管理系统后端时,可能会用到许多关键类,包括控制器类、服务类、DAO类、实体类等。以下是一些后端开发过程中可能是用到的关键类:
控制器类:控制器类主要负责接受用户请求,调用相应的服务类完成业务逻辑的处理,并将处理结果返回给前端页面。例如,可以根据业务需求设计房源控制器类、订单控制器类等。
服务类:服务类主要负责业务逻辑的处理,包括对数据的读取、修改、删除等操作。例如,可以设计房源服务类、订单服务类等。
DAO类:DAO(Data Access Object)类主要负责数据访问操作,与数据库交互并提供基本的CRUD(Create, Read, Update, Delete)操作。例如,可以设计房源DAO类、订单DAO类等。
实体类:实体类代表了系统中的各种对象,包括房源、订单、用户等等。这些实体类通常包含实体属性、构造方法以及与数据库中表的映射关系,用于实现对象的持久化存储和操作。
除此之外,还可能会使用到工具类、配置类等,用于实现系统中的各种辅助功能。例如,可以使用MyBatis来实现数据库访问,使用Redis等缓存技术提高系统性能,使用Spring Security等安全框架来实现权限控制。
在设计关键类时,需要充分考虑到系统的业务需求和技术实现,遵循面向对象编程的原则,使得系统的代码结构简洁、可读性好、易于维护。
== 本章小结
本章通过对房屋租赁系统的分析,结合实际的工作情况,对房屋租赁系统设计的工作方面,包括前端部分和后端部分三个模块进行了介绍。
= 系统实现
== 开发环境
选择合适的开发工具与语言可以有效的提升开发效率。
=== 软件环境
==== Visual Studio Code
Visual Studio Code,也被简称为VS Code,是一款免费、开源、轻量级的集成开环境(IDE)。由软于2015年发布,现已成为一款颇受开发者喜欢的代码编辑器。Visual Studio Code有以下的优点:
+ 语言支持:VS Code支持数十种编程语言,包括JavaScript、TypeScript、Python、Java等。它能通过插件市场获取更多语言支持。
+ 调试工具:VS Code拥有内置的试器,支持Node、TypeScript和JavaScript的调试通过插件市场,可以获取其他语言的调试器。
+ 智能代码提示:VS支持自动补全、变量定义跟踪等功能,能够提高开发效率。
+ 版本控制:VS Code支持Git和SVN等版本控制系统,可以直接在编辑器中进行版本管理。
+ 扩展性: Code支持丰富插件生态,用户可以通过插件市场获取各类插件,例如风格检查、项目等。
+ 跨平台:VS Code支持Windows、macOS和Linux操作系统。
由此看来,Studio Code以其简洁易用、功能强大、跨平台等特点受到越来越多开发者的推崇,并成为全球范围内非受欢迎的代码编辑器。
==== IDEA
IDEA是JetBrains公司开发的一款Java IDE,优秀的代码编辑器和调试工具。它支持多种编程语言,包括Java、Kotlin、Groovy、Scala等。IDEA是基于IntelliJ IDEA Community Edition打的,具有轻量且易于学习的特点。
IDEA提供了智能代码补全、重构、代码分析、版本控制以及其他实用工具,使得开发者可以更加有效地进行开发这款IDE还包括量的插件,例如UI设计器、数据库管理、Web开发,这些插件可以帮开发人员进一的提高开发效率。
与其他IDE相比,IDEA在代码提示、Refactor等方面表现越,并且具有强大的搜索功能和快捷键设置。好的辅助功能使得IDEA为Java开发者的选IDE之一。
总之,作为业界标准之一的Java开发工具之一,IDEA在提高编写效率、缩短开发周期等面具有重要作。
==== MySQL数据库
MySQL是一个广泛使用的关系型数据库管理系统,开源免费。MySQL是轻量级且易于安装部署,在开发Web应用非常流行。MySQL持多种操作系统,并可以通过多种编语言进行访问。MySQL功能丰富,提供了完整的数据管理、查询和处理功能,可以存储大型数据集并支持高并发访问。MySQL的安全性也得到了很好的保证,支持基于角的访问控制和、表、列级别的权限管理。
==== Navicat
Navicat是一款功能强大的数据库管理工具,支持多种数据库管理系统,例如MySQL、MariaDB、Oracle、PostgreSQL等,也包括多种操作系统,例如:Windows、macOS、Linux等。Navicat是一款商业软件,提供了丰富的和全面的性能优化,旨在帮开发者更加高地管理和维护数据库。
=== 硬件环境
操作系统:Windows 10
处理器:Intel(R) Core(TM) i5-8300H CPU
显卡:NVIDIA GeForce GTX 1060
== 前端实现
=== 界面设计
+ 登录界面:需要输入用户名,密码以及验证码登录。
#image("img/login.png", width: 70%)
#image("img/register.png", width: 70%)
+ 用户管理面:管理员可以查看和管理所有用户的信息,包括注册时间、联系方式等。
+ 房源管理界面:管理员可以查看和管理所有房源的,包括图片、描述价格、位置等,并能对新增、更新或删除房源信息。
+ 订单管理界面:管理员可以查看和管理所有订单的信息,包括订单状态、支付情况等,并能对订单进行审核或取消。
+ 系统设置界面:管理员可以针对系统进行相关设置,如邮件通知、短信提醒等。
+ 日志管理界面:管理员可以查看系统运行日志及操作日志。
+ 权限管理界面:管理员可以管理系统用户的权限,分配不同角色和权限。
+ 数据备份和恢复界面:管理员可以进行数据库备份和恢复操作。
=== 功能设计
+ 注册界面:没有登陆过的用户先要注册了之后才能登陆。需要输入手机号、姓名、密码,并通过图片验证码才能进行注册。
+ 用户管理面:管理员可以查看和管理所有用户的信息,包括注册时间、联系方式等。
+ 房源管理界面:管理员可以查看和管理所有房源的,包括图片、描述价格、位置等,并能对新增、更新或删除房源信息。
+ 订单管理界面:管理员可以查看和管理所有订单的信息,包括订单状态、支付情况等,并能对订单进行审核或取消。
+ 系统设置界面:管理员可以针对系统进行相关设置,如邮件通知、短信提醒等。
+ 日志管理界面:管理员可以查看系统运行日志及操作日志。
+ 权限管理界面:管理员可以管理系统用户的权限,分配不同角色和权限。
+ 数据备份和恢复界面:管理员可以进行数据库备份和恢复操作。
=== 动态设计
+ 响应式设计:现在越来越多的人使用手机和平板电脑上网,因此,一个好的房屋租赁管理系统必须具备响应式设计,以适应不同设备的屏幕尺寸和分辨率。通过这种方式,用户可以随时随地访问系统而不必担心屏幕尺寸或布局问题。
+ 数据可视化:一个好的房屋租赁管理系统应该具有良好的数据可视化功能,以帮助用户更好地了解租赁业务的状况。例如,可以使用柱状图或折线图等方式展示关于租户数量、租金收入和支出等关键指标的数据。这样,用户可以通过数据可视化快速评估其租赁业务的运营状况。
+ 自动化流程:一个好的房屋租赁管理系统还应该具备自动化的流程,以提高用户的工作效率。例如,当一份合同到期时,系统应该能够自动提醒用户需要更新合同,而不必手动查找过期合同。这种自动化流程可以帮助用户大大减少操作时间和精力。
+ 安全性:一个好的房屋租赁管理系统必须具备安全性。租赁管理系统通常包含很多敏感数据,例如租客的个人信息和账单信息等,因此必须确保这些数据不会被未经授权的第三方访问或泄露。系统应该采用加密方法来保护存储在数据库中的信息,同时还应该设定权限系统,以限制每个用户可以访问的数据量和范围。
#image("img/lock.png")
总之,房屋租赁管理系统是一个非常重要的应用程序,可以帮助房地产公司、物业管理公司和个人房东等有效管理其租赁业务。通过考虑响应式设计、多语言支持、数据可视化、自动化流程以及安全性等关键因素,可以确保该系统具有良好的用户体验,并能够在市场上获得成功。
== 后端实现
后端部分使用了Java的SpringBoot框架,并且采取的MySQL数据库来存储数据。大体步骤如下:
- 先搭建一个SpringBoot项目,使用了IDEA开发工具来进行后端开发。
- 确定系统架构和数据库结构,设计ER图创建相应的表格
- 在pom.xml文件中添加必的依赖,包括 Boot和MySQL驱动。
- 编实体类(Entity)和DAO层(Data Access Object)对应的Repository接口,以及对应的SQL语句。
- 创建服务层(Service)并实现事务管理。
- 配置数据库连接池和相关的参数,包括数据库url、用户名和密码等。
- 编写控制层(Controller)及相应的API接,提供相应的增删改查功能。
- 进行单元测试和成测试,保证功能常。
- 部署项目到服务器上,让用户能够直接使用并进行后续维护。
#image("img/idea1.png")
#image("img/idea2.png")
#image("img/idea3.png")
#image("img/idea4.png")
#image("img/idea5.png")
#image("img/idea6.png")
#image("img/idea7.png")
== 后端开发的关键类
在使用Spring Boot框架中实现功能有许多关键类,下面将介绍部分关键类。
1. \@RestController: 注解表示该类是一个RESTful API的控制器。
2. \@RequestMapping: 该注解表示该方法对应的URL请求路径。
3. \@RequestBody: 该注解表示该参数是请求体中的数据。
4. \@Autowired: 该注解表示该属性需要自动注入某个对象。
5. JpaRepository: 该接口提供了很多通用的数据库操作方法
6. \@Entity: 该注解表示该类应数据库中的一张表。
7. \@Table: 该注解表示该类对应数据库中的一张表,来指定表的名称和其它属性。
8. \@GeneratedValue: 该注解表示该属性的值数据库自动生成。
9. \@Id: 该注解表示该属性是实体类的主键。
10. \@Column:该注解表示该属性对应数据库中的一列,用来指定字段的名称和其它属性。
11. \@: 该注解表示方法执行时需要开启一个事务。
12. \@Modifying: 该注解表示该方法执行时需要修改数据库中的数据。
=== 数据库设计
#figure(
caption: [category表],
kind: table,
supplement: "表",
easytable({
let tr = tr_alt
cwidth(1fr, 1fr, 1fr)
cstyle(left, center, right)
th[Header 1][Header 2][Header 3]
tr[How][I][want]
tr[a][drink,][alcoholic]
tr[of][course,][after]
tr[the][heavy][lectures]
tr[involving][quantum][mechanics.]
}),
)
=== 接口设计
勾股定理可用公式:$a^2 + b^2 = c^2$表示。
#figure(
caption: [数列求和],
kind: math.equation,
supplement: "公式",
$ sum_(k=1)^n k = (n(n+1)) / 2 $,
)
== 本章小结
本章结束了房屋租赁管理系统的所需的硬件环境。对前端页面和后端的具体实现进行了介绍。同时,对后端关键类的实现方法进行了阐述。
= 系统测试与运行
== 测试
软件测试通常是指验证与确认两部分。该系统的主要进行了以下几个方面的测试:资源测试、功能测试、任务测试。测试的流程 @fig:testflow 所示。
#figure(
caption: [测试流程],
image("img/testflow.png", width: 50%),
) <testflow>
=== 资源测试
房屋租赁管理系统的资源测试是对系统进行性能,以确保系统在高负载、大流量情况下仍然能够稳定运行。下面介绍具体的测试内容和流程:
1. 负载测试:这种测试通过模拟用户并发问系统,同时观察系统响应时间、吞吐量等指标来评估系统在承受并发请求时的能力。测试时需要针对不同的业务场景(例如搜索房源、订单、支付等)进行测试,并分别记录响应时间请求成功率、错误码等指标。
2. 压力测试:将系统负载逐渐增加,直到达到系统极限,观察系统在极端情况下的表现。测试阶段需要设定并观察系统响应时间、CPU利用率、内存使用量、带宽利用率等关键指标,以保证系统在硬件资源撑不住的情况下和内部逻辑出现瓶颈的能保持应有的能和稳定性。
3. 并发测试:模拟多个用户并发访问同一个页面或接口,以检测系统在高并发情况的表现。并发测试数据需要根据业务特点精确制定,去模拟正常和异常下的并发请求比如打开一个页面,提交同一个表单,支付多少订单,同时踢出多少用户等。
4. 数据量测试:将大数据导入系统中进行测试,以检验系统的性能和稳定性。测试过程中需要特别关注系统在数据查询、更新、删除等操作时表现,同时还需要注内存和CPU利用率的变化趋势;
5. 日志跟踪测试:通过记录系统日并进行分析,可以踪系统在某个时间段或者某个业务场景下执行的情况。这种测试可以发现系统运行时出现的异常、慢查询和错误。
经过以上测试,可以获取到系统各方面的性能参数与指标从而进行较好的化和调整。
=== 功能测试
房屋租赁管理系统的功能测试是对系统进行项功能方面的测试,以保证系统满足需求并能正常运行。下面具体是测试内容的流程:
1. 用户管理功能测试:测试系统能否正确地实现用户账号注册、,个人信息修改和找回等功能,并检查这些功能的安全性和稳定性。
2. 房源管理功能测试:测试系统能否支持房源的添加、修改、查询和删除等操作,并能够准确地显示房源信息,同时测试系统搜索功能是否准确返回相应搜索结果。
3. 租户管理功能测试:测试系统能否支持租户信息注册、修改和删除等操作,并能准确地记录租房合同信息,租金缴纳情况和租房状态信息。
4. 订单管理功能测试:测试系统能否自动生成订单且订单信息的准确性,订单状态处理的准确性。
5. 支付功能测试:测试系统是否支持多种支付渠道,能够安全地处理付款信息,管理退款信息。
6. 系统管理功能测试:测试系统管理功能包括系统日志记录、数据备份和恢复,网站SEO、营销推广等部分,以及其他额外功能如系统主题切换、语言转等。
经过以上测试笔者们可以确认系统各项功能的完整性和质量,确保系统能够足用户的需求并能够稳定运行。
== 运行界面
经过测试与修改以后,系统就可以正常运行了。@fig:login 显示用户进入系统的登录界面。
#figure(
caption: [登录界面],
image("img/login.png"),
) <login>
@fig:register 表示注册界面
#figure(
caption: [注册],
image("img/register.png"),
) <register>
@fig:home 表示用户的主页面
#figure(
caption: [主页面],
image("img/home.png"),
) <home>
@fig:manage 表示用户管理界面
#figure(
caption: [管理界面],
image("img/manage.png"),
) <manage>
== 本章小结
本章主要介绍了系统测试以及最终系统运行结果。首先介绍了这个测试流程,包括资源测试和功能测试。通过系统实际运行页面截图,辅以文字描述对系统的最终运行结果进行了效果展示说明。
= 总结
本篇论文主要介绍了房屋租赁管理的系统与实现,通过对系统的详细描述和体实现,展现了其在房屋租赁管理中的重要作用。
首先介绍了课题的背景和研究意义,指出了房屋租赁管理系统的必要性和重性。接下来,本文分析了当前房屋租赁行业的现状和问题,并提出了本文设计的系统解决问题的方法。房屋租赁管理设计和实现基于Java,使用SpringBoot开发框架进行开发,并采用MySQL数据库进行数据管理。通过对用户需求的分析和系统功能的划分,本文实现了系统的基础功能和高级功能,包括房屋信息管理、租客信息管理等核心模块。
在具体实现中,采用了MVC模式,将系统的业务逻辑、视图呈现和数据处理相互分离,从而提高了系统的可重用性、可扩展性和可维护性。
最后通过对本文设计和实现的总结,可以得出如下结论:
1. 房屋租赁管理系统的设计和实现有效提高房屋租赁行业的管理效率服务质量,满足用户需求,为用户带来更好的服务体验。
2. 本文所采用的设计方法和技术手段是有效的,被应用于类似的管理系统的开发中,并具一定的普适性。
3. 本文的研究仍然存在一些不足之处,例如对用户需求的分析不够深入,系统安全性的处理还完善等,这些问题需要在今后的研究中得到进一步的完善和改进。
综上所述,本文的研究为房屋租赁管理系统的设计和实现提供了一定的参考和借鉴值,也为相关领域的研究者提供了一点微薄之力。
#counter(heading).update(0)
#set heading(numbering: "A.1")
= 附录
您可在#link("https://github.com/soarowl/geelypaper.git")检查最新代码,或提PR。
== 论文模板
#raw(read("paper.typ"), lang: "typc", block: true)
== 本文代码
#raw(read("paper_demo.typ"), lang: "typc", block: true)
#bibliography("basic.yml", style: "gb-7714-2015-numeric")
#set heading(numbering: none)
= 致#h(2em)谢
在笔者的本科生涯即将结束之际,笔者不禁回首往事,深感时光如梭。这些年来有许多人和事让笔者受益匪浅,使得笔者度过了充实而难忘的四年。在这篇毕业论文致谢中,笔者要对他们表达真情实感的感激之意。
首先,笔者要感谢笔者的父母,在笔者茁壮成长的过程给予了笔者无尽的关爱和支持。他们默默无闻地为笔者付出,从小到大笔者一直被他们宠了。他们为了笔者能够顺利完成学业,所有的膳食语出等供应都是最好的,虽然这些都可能已成为家长义务但是,对于笔者感恩永存。
其次笔者要感谢笔者的导师卓能文老师,他是一个温暖、善良且富有智慧的人。他为笔者们的实项目指明了前进方向,耐心细致地给予指导和帮助。在研究过程中遇到困难和障碍时,他会及时指出问题所在并提出建设性意见。虽然笔者只是一名徒弟,但他从始至终给笔者的关怀和帮助让笔者受益匪浅。
再次,笔者要感谢笔者的同学们,你们是笔者路走来的陪伴者。在学习中若遇到困难,你们会及时贡献自己的智慧和时间来帮助笔者解决问题。在生活每次共同的经也能让笔者感到非常快乐。与你们在一起的时光不仅是笔者难忘的回忆,也是让笔者成长的催化剂。笔者将永远怀念笔者们一起度过的岁月。
此外,笔者还要感谢吉利学院为笔者提供的良好学习和交流环境。无论从课程设置、图书馆资源和学术研究都给了笔者很大的帮助。在这里,笔者收获了知识和思方式,找到了未职业发展的方向。
最后,笔者还要感谢笔者的朋友们,谢谢你们的建议和支持。你们用你们的话语温暖笔者,在笔者孤独时在笔者身边陪伴,让笔者感到自己是个幸运的人。
总之,笔者的日记本永远记录着与你们共进退的日子,未来笔者们无论在世界的哪个角落,未来笔者们依然并行不悔。上天在笔者人生路上给予笔者许多的善意希望笔者们能够再次相遇在人生旅途的某处。感谢你们,祝笔者们回首枯藤老树时,仍是少年郎!
|
|
https://github.com/jgm/typst-hs | https://raw.githubusercontent.com/jgm/typst-hs/main/test/typ/meta/document-04.typ | typst | Other | // Error: 10-12 can only be used in set rules
#document()
|
https://github.com/jamesrswift/musicaux | https://raw.githubusercontent.com/jamesrswift/musicaux/main/src/cmd.typ | typst | #import "commands/basic-content.typ": *
#import "commands/common.typ"
#import "commands/bars.typ"
#import "commands/environments.typ" as env;
#import "commands/time.typ" |
|
https://github.com/oravard/typst-dataframes | https://raw.githubusercontent.com/oravard/typst-dataframes/main/README.md | markdown | MIT License | # dframes: DataFrames for typst
This packages deals with data frames which are objects that are similar to pandas dataframes in python or DataFrames in Julia.
A dataframe is a two dimentionnal array. Many operations can be done between columns, rows and it can be displayed as a table or as a graphic plot.
## Simple use case
A dataframe is created given its array for each column. Displaying the dataframe can be done using `plot` or `tbl` functions:
```typst
#import "@preview/dataframes:0.1.0": *
#let df = dataframe(
Year:(2021,2022,2023),
Fruits:(10,20,30),
Vegetables:(11,15,35)
)
Stocks:
#tbl(df)
#plot(df, x:"Year", x-tick-step:1)
```
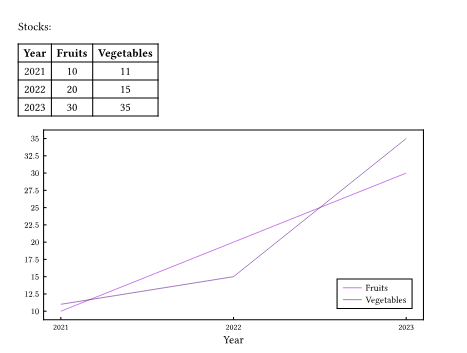
## Dataframe creation
The simple way to create a dataframe is to provide arrays with their corresponding column names to the constructor like in the preceding paragraph.
But, you can provide each lines of your dataframe as an array. This means that you have to specify the column names for each line. The following example is equivalent to the preceding one.
```typst
#let adf =(
(Year:2021, Fruits:10, Vegetables: 11),
(Year:2022, Fruits:20, Vegetables: 15),
(Year:2023, Fruits:30, Vegetables: 35),
)
#let df = dataframe(adf)
//is equivalent to
#let df = = dataframe(
Year:(2021,2022,2023),
Fruits:(10,20,30),
Vegetables:(11,15,35)
)
```
The specification of a dataframe is that the number of elements for each column must be the same. If this is not the case, an error is raised.
For the following explainations, we will use `df` as the dataframe which is defined in this paragraph.
## Rows and columns
Columns are accessed using dot following by the column name (ex: `df.Year` returns the column "Year" of the dataframe). Rows can be selected using the `row` function (ex: `row(df,i)` returns the ith row of df). Selecting a set of rows and columns can be done using `slice` or `select` functions.
Rows and columns can be added with `add-cols` and `add-rows` functions or by concatenation of two dataframes using `concat`.
### nb-rows
The function `nb-rows` returns the number of rows of a dataframe:
```typst
#let nb = nb-rows(df)
#nb
```
displays:
```
3
```
### nb-cols
The function `nb-cols` returns the number of columns of a dataframe.
```typst
#let nb = nb-cols(df)
#nb
```
displays:
```
3
```
### size
The function `size` returns an array of (nb-rows,nb-cols).
```typst
#let nb = size(df)
#nb
```
displays:
```
(3,3)
```
### add-cols
The function `add-colls` add columns to the dataframe. Columns are provided with their column name as named arguments.
```typst
#let df = add-cols(df, Milk:(19,5,15))
#tbl(df)
```
displays:
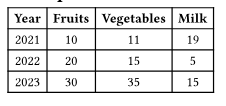
a shortcut `hcat` to `add-cols` is provided for people who are more confortable with Python or Julia terminology.
### add-rows
The function `add-rows` add rows to the dataframe. Rows are provided as named arguments. Each argument could be a scalar or an array. The only rule is that the final number of elements for each columns is the same.
```typst
#let df2 = add-rows(df,
Year:2024,
Fruits:25,
Vegetables:20,
Milk:10)
#tbl(df2)
#let df3 = add-rows(df,
Year:(2024,2025),
Fruits:(25,30),
Vegetables:(20,10),
Milk:(10,5))
#columns(2)[
#tbl(df2)
#colbreak()
#tbl(df3)]
```
displays:
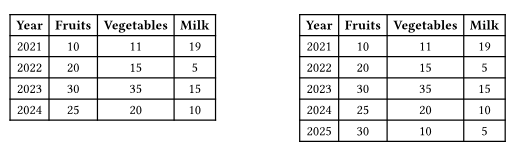
If the arguments of function `add-rows` do not provides each columns, the missing elements are replaced with the `missing` value:
```typst
#let df2 = add-rows(df, Year:2024, Fruits:25, Vegetables:20)
#let df3 = add-rows(df, Year:2024, Fruits:25, Vegetables:20, missing:"/")
#columns(2)[
#tbl(df2)
#colbreak()
#tbl(df3)]
```
displays:
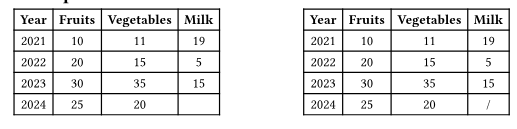
Be carreful using the `missing` argument which default is `none`. Future numerical operations using rows / cols will raise an error. Provide a numerical value for the `missing` argument if you want to do future numerical operations between rows / cols.
a shortcut `vcat` to `add-rows` is provided for people who are more confortable with Python or Julia terminology.
### concatenation
The concatenation of two dataframes can be done using the `concat` function. The `concat` function takes two dataframes as arguments. The result is a dataframe using the following rules:
- if the column names of the two dataframes are the same, the second dataframe is added to the first as new rows.
- if all column names of the second dataframe are different of the first dataframe column names, the second dataframe is added to the first as new columns. It implies that the number of rows of the two dataframes are the same.
```typst
#let df = dataframe(
Year:(2021,2022,2023),
Fruits:(10,20,30),
Vegetables:(11,15,35)
)
#let df2 = dataframe(
Year:2024,
Fruits:25,
Vegetables:20
)
#let df3 = dataframe(Milk:(19,5,15))
#columns(2)[
#tbl(concat(df,df2))
#colbreak()
#tbl(concat(df,df3))
```
displays:

The dataframe `df2` is equivalent to adding row to `df` while `df3` is equivalent to adding column to `df`.
### slice
The `slice` function allows to select rows and cols of a dataframe returning a new dataframe. The arguments of the `slice` function are:
- `row-start`: the first row to return (default:0)
- `row-end`: the last row to return (default: none -> the last)
- `row-count`: the number of rows to return (default: -1 -> row-end - row-start)
- `col-start`: the first col to return (default:0)
- `row-end`: the last col to return (default: none -> the last)
- `row-count`: the number of cols to return (default: -1 -> col-end - col-start)
Example :
```typst
#tbl(slice(df, row-start:1, col-start:1))
```
displays:
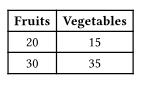
### select
The select function allows to select rows or columns.
- rows are selected given their name or a filter function
- cols are selected given a filter function
The arguments of the `select` function are:
- `rows` : (default:`auto`) a filter function which return `true` for all desired rows.
- `cols`: (default:`auto`) an array of col names or a string of col name or a function which returns `true` for the desired cols.
Example:
```typst
#let df2 = select(df, rows:r=>r.Year > 2022)
#let df3 = select(df, cols:r=>r!="Fruits")
#tbl(select(df, cols:("Fruits","Vegetables"),
rows:r=>r.Year > 2022))
```
### sorted
The `sorted` function allows to sort a dataframe. The arguments are:
- `col`: the column name for sorting (ascending)
- `rev`: (default:`false`) `true` for reverse mode (descending)
Example:
```typst
sorted(df,"Year",rev:true)
```
## Numerical operations
Many operations can be done on dataframes. We have four kind of operations: unary, two elements, cumulative and folding.
### Unary operations
An unary operation make the same operation on all elements of a dataframe. Here is the list of available unary operations:
| Function name | Description |
|---------------|-------------|
| `abs` | returns the absolute value (ex: `abs(df)`)|
| `ceil` | returns the nearest greter integer|
| `floor` | returns the nearest smaller integer|
| `round` | returns the rounding value. You can use the named argument `digits` (ex: `round(df,digits:2)`) |
| `exp` | returns exponential value |
| `log` | returns the logarithmic value |
| `sin` | returns sinus |
| `cos` | returns cosinus |
### Two elements operations
For example, some elements can be added to a dataframe using the `add(df,other)` function. We consider four cases for this kind of operation :
- if `other` is a scalar: `other` is added to all efements of `df`
- if `other` is a dataframe:
- if `other` number cols is 1, then each col of `df` is added term by term with `other`
- if `other` number cols is equal to `df` number cols, each col of `df` is added term by term to the col of `other` with the same index
- if `other` column names are equal to `df` column names, each col of `df` is added term by term to the col of `other` which have the same name.
Example:
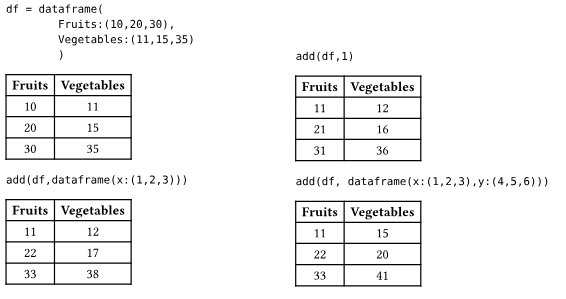
These rules applies to all the following two elements functions:
| Function | Description |
|-----------|--------------|
|`add` | Addition `add(df,other)` |
|`substract`| Substraction `substract(df,other)`|
|`mult` | Multiplication `mult(df,other)` |
|`div` | Division `div(df,other)` |
### Cumulative operations
A cumulative operation on a dataframe is an operation where each row (or col) is the result of an operation on all preceding rows (or cols).
Each cumulative operation take a dataframe `df` as positional argument and `axis` as named argument. If `axis:1` (default), the operation is made on rows and if `axis:2`, the operation is made on columns.
The cumulative operations are the following:
|Function | Description |
|-|-|
|`cumsum`| Cumulative sum|
|`cumprod`| Cumulative product|
Example:
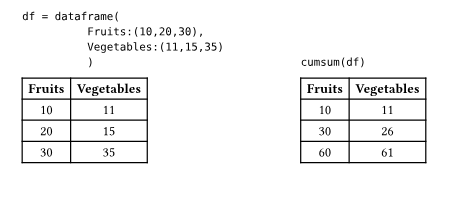
### Folding operation
A folding operation is an operation which result in one row (or col) using a folding operation. For example, the `sum(df)` function on a dataframe `df` will give a row with each element is the sum of the corresponding `df` col.
Each folding operation take a dataframe `df` as positional argument and `axis` as named argument. If `axis:1` (default), the operation is made on rows and if `axis:2`, the operation is made on columns.
The folding operations are the following:
|Function | Description |
|-|-|
| `sum` | sum of all elements of each column or row |
| `product` | product of all elements of each column or row |
| `min` | minimum of all elements of each column or row |
| `max` | maximum of all elements of each column or row |
| `mean` | mean value of all elements of each column or row |
Example:
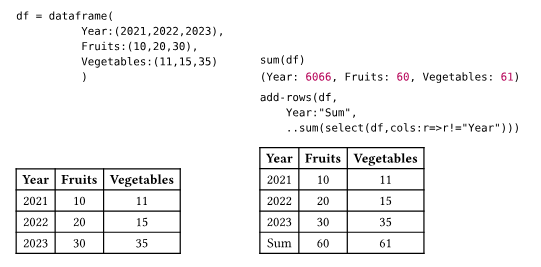
### Other operations
|Function | Description |
|-----------|-|
|`diff(df,axis:1)`| Compute the difference between each element of `df` and the element in the same column (row if `axis:2`) and preceding row (column if `axis:2`)
## Dataframe from CSV
Dataframes can be created from a CSV file using the `dataframe-from-csv` function which takes a `CSV` object as positional argument.
The `dataframe-from-csv` use the `tabut` package but, in addition, this function supports datetime fields.
Example:
```typst
#let df = dataframe-from-csv(csv("data/AAPL.csv"))
#tbl(slice(df, row-end:5))
```
displays:
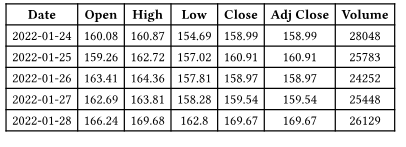
## Display a dataframe as table
the `tbl` function displays the dataframe as a typst table. This function use the `tabut` function of the `tabut` package. All named argument as passed to the `tabut` function.
Example: display transposed dataframe
```typst
#let df = slice(dataframe-from-csv(csv("data/AAPL.csv")),row-end:5)
#tbl(df, transpose:true)
```
displays:
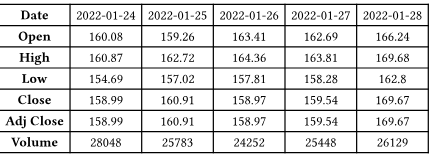
if you want to specify more display details using `tablex` (as an example), the `tabut-cells` is available for dataframes.
All arguments are passed to `tabut-cells` function.
See `tabut` package documentation for more details.
Example:
```typst
#let df = dataframe(
Year:(2021,2022,2023),
Fruits:(10,20,30),
Vegetables:(11,15,35)
)
#import "@preview/tablex:0.0.8":*
#tablex(
..tabut-cells(df,
(
(header: "Year", func:r=>r.Year),
(header:"Fruits", func:r=>r.Fruits)
),
headers:true
))
```
displays:
For more informations about using `tabut-cells` function, see the `tabut` package documentation.
## Display a dataframe as plot
The `plot` function allowed to plot dataframes. Each column of the dataframe is a curve labeled in a legend by their column name. x-axis is the dataframe index if it is not provided in arguments, but a specified column can be used as x-axis which supports datetime.
The plot is build using the `cetz` package. All default parameters are chosen in order to have a scientific standard look and feel, but additionnal parameters are transmitted to `cetz` functions.
```typst
plot(df, x-label:none,
y-label:none,
y2-label:none,
label-text-size:1em,
tick-text-size:0.8em,
x-tick-step:auto,
y-tick-step:auto,
y2-tick-step:auto,
x-tick-rotate:0deg,
x-tick-anchor:"north",
y-tick-rotate:0deg,
y-tick-anchor:"east",
y2-tick-rotate:0deg,
y2-tick-anchor:"west",
x-minor-tick-step:auto,
y-minor-tick-step:auto,
y2-minor-tick-step:auto,
x-min:none,
y-min:none,
x-max:none,
y-max:none,
x-axis-padding:2%,
y-axis-padding:2%,
axis-style:"scientific",
grid:false,
width:80%,
aspect-ratio:50%,
style:(:),
legend-default-position:"legend.inner-south-east",
legend-padding:0.15,
legend-spacing:0.3,
legend-item-spacing:0.15,
legend-item-preview-height:0.2,
legend-item-preview-width:0.6,
..kw)
```
| <div style="width:220px">Argument</div> | Description |
|-|-|
|`df`| The dataframe to display |
|`x`| The column name for the x-axis. By default, the dataframe index is used. x-axis column name can be datatime objects. In this case, tick labels are displayed using datetime.display(). x-axis can be a column which contains strings. In this case, the strings appears as x-tick labels and `x-tick-step` has no effect. |
|`y`| The curves to plot as y-axis. By default, all columns of the dataframe are plotted. `y` can be an array of column names to plot. |
|`x-label`| The label on x-axis. By default, `x-label` is the column name of the chosen column for x-axis. |
|`y-label`| The label on y-axis. By default, no label. |
|`y2-label`| The label on y2-axis. By default, no label. |
|`label-text-size`| The text size of x-label and y-label. |
|`tick-text-size`| The text size for tick labels. |
|`y-tick-step`| The separation between y axis ticks. |
|`y2-tick-step`| The separation between y2 axis ticks. |
|`x-tick-step`| The separation between x axis ticks. If the dataframe column chosen for x-axis contains datetimes, `x-tick-step` must be a duration object.|
|`x-tick-rotate`| An angle for x-tick rotation. |
|`x-tick-anchor`| Anchor of the x-tick labels ("north","south","west", "east", "center"). Useful when `x-tick-rotate` is used. |
|`y-tick-rotate`| An angle for y-tick rotation. |
|`y-tick-anchor`| Anchor of the y-tick labels ("north","south","west", "east", "center"). Useful when `y-tick-rotate` is used. |
|`y2-tick-rotate`| An angle for y2-tick rotation. |
|`y2-tick-anchor`| Anchor of the y2-tick labels ("north","south","west", "east", "center"). Useful when `y2-tick-rotate` is used. |
|`x-minor-tick-step`| The separation between minor x axis ticks. |
|`y-minor-tick-step`| The separation between minor y axis ticks. |
|`y2-minor-tick-step`| The separation between minor y2 axis ticks. |
|`x-min`| The min value for x-axis. It has no effect if the dataframe column chosen for x-axis contains strings. If the dataframe column chosen for x-axis contains datetime objects, `x-min` must be a datetime object. |
|`y-min`| The min value for y-axis |
|`x-max`| The max value for x-axis. It has no effect if the dataframe column chosen for x-axis contains strings. If the dataframe column chosen for x-axis contains datetime objects, `x-max` must be a datetime object. |
|`y-max`| The max value for y-axis. |
|`grid`| `true` to draw a grid for both x and y-axis. |
|`width`| The width of the canvas plot. An absolute or relative length which default is 80%. |
|`aspect-ratio`| The ratio height/width of the plot canvas. A ratio object which default is 50%. |
|`style`| A dictionary which defines each curve plot style. It is indexed by column names of the dataframe. Each value of this dictionary is also a dictionary with the following allowed keys: <BR> `color`: the color of the curve. Any values accepted by `cetz` is allowed.<BR> `label`: the label of the curve. By default label is the column name of the dataframe.<BR> `thickness`: the thickness of the curve. 0.5pt by default.<BR> `mark`: the mark for each point of the curve. By default, no mark but any character is allowed in addition to any value accepted by `cetz`.<BR>`mark-size`: the size of the mark. 0.15 by default.<BR>`dash`: `none`, `dashed`, `dotted` or any value accepted by `cetz`.<BR>`axes`: specifies which axes should be used for the given curve `("x","y")` for bottom / left axis and `("x","y2")` for bottom/right axis. <BR>In addition, any argument which is accepted by `cetz` will be passed to the `cetz.plot.add` function. |
|`legend-default-position`| Legend default position. All values accepted by `cetz` for legend position are allowed. |
|`legend-padding`| Space between the legend frame and and content. Default: 0.15 |
|`legend-spacing`| Space between the legend frame and plot axis. Default: 0.3|
|`legend-item-spacing`| Space between legend items. Default: 0.15|
|`legend-item-preview-height`| Height of each legend previews. Default: 0.2|
|`legend-item-preview-width`| Width of each legend previews. Default: 0.6|
| `kw` | additionnal arguments passed to `cetz.plot.plot` function. See `cetz` documentation for more information on available arguments. |
Example:
```typst
#let df = dataframe-from-csv(csv("data/AAPL.csv"))
#plot(df, x:"Date",
y:("Close","High","Low"),
x-tick-step:duration(days:5),
x-tick-rotate:-45deg, x-tick-anchor:"west",
style:(
"Close": (color:red, thickness:1pt, mark:"o", line:"spline"),
"Low":(color:rgb(250,40,0,100),hypograph:true, thickness:2pt),
"High":(color:rgb(0,250,0,100),epigraph:true, thickness:2pt)
))
```
displays:
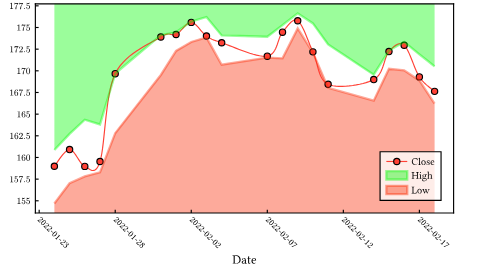 |
https://github.com/heytentt/typst-cv | https://raw.githubusercontent.com/heytentt/typst-cv/main/cv-cn.typ | typst | MIT License | /* Global settings */
// #show link: underline
#set page(margin: (x: 1.5cm, y: 1.5cm))
#set par(
leading: 0.8em,
justify: true,
)
#set text(font: ("SimSong"), size: 11pt)
/* Functions */
#let h1(body) = {text(size: 17pt, font: "Songti SC", weight: "bold")[#body]}
#let h2(body) = {text(size: 13pt)[#body]}
#let h3(body) = {text(size: 11pt, font: "Songti SC", weight: "bold")[#body]}
#let small(body) = {text(size: 10pt)[#body]}
#let bold(body) = {text(font: "Songti SC", weight: "bold")[#body]}
#let xline() = {v(-8pt); line(length: 100%); v(-3pt)}
#let section-title(body) = {
v(5pt)
h2[#body]
xline()
}
#let zsection(body) = { grid(columns: (10pt, 1fr))[][#par(leading: 0.75em)[#body]]; v(3pt) }
/* Content */
#h1[张三]
#v(-5pt)
12312341234 | <EMAIL> | #link("https://github.com/zhangsan")[github.com/zhangsan]
#section-title[教育背景]
- #h3[中国山河大学] #h(1fr) 山东 河南 \
#v(-3pt)
#zsection[
计算机不科学(学士)#h(0.5cm)#small[绩点 0.4(200/250),多次荣获山河四省鼓励奖学金] #h(1fr) 2000/09 -- 2004/06 \
计算机很科学(硕士)#h(0.5cm)#small[一篇 CCF Z 类文章] #h(1fr) 2004/09 -- 2007/06 \
]
- #h3[中国社会大学] #h(1fr) 安徽 南京 \
#v(-3pt)
#h(0.3cm) 猫的流体力学研究(博士)#h(0.2cm)#small[获得 2023 搞笑诺贝尔奖] #h(1fr) 2007/09 -- 2010/06 \
#section-title[研究经历]
- #h3[咖啡因对创造力的影响] #h(1fr) 山河大学次时代研究所
#v(-4pt)
#zsection[我们进行了一项随机对照实验,探究了咖啡因对创造力的影响。通过给参与者不同剂量的咖啡因后进行创造性任务的评估,我们发现适量的咖啡因能够显著提升创造力水平,为理解咖啡因对认知功能的影响提供了实证支持。]
- #h3[猫咪的睡眠行为与梦境研究] #h(2fr) 山河大学白日梦研究所
#v(-4pt)
#zsection[在研究期间,我带领着一支勇敢的研究小组,深入探索了猫咪的睡眠行为与梦境之间的神秘联系,这项研究成果不仅能够让人们更好地照顾和理解自己的宠物,还有望为人类的睡眠障碍研究提供新的思路和启示。]
#section-title[实习经历]
#h3[快乐游戏有限公司] #h(1fr) 2010/07 -- 2013/10 \
- #bold[笑话筛选挑战]:负责阅读大量笑话并进行评估,只有笑出肚子痛的才能通过。每次笑出声都会有同事以"哈哈奖"激励,但副作用是喝水时总会喷出来。
- #bold[研发新奇笑话]:参与团队的创新项目,努力开发出新颖有趣的笑话。但有时候创意会突然消失,只能在办公室角落寻找,有时幸运会发现它藏在打印机里。
#section-title[开源项目]
#h3[笑话生成器] #h(0.3cm)#link("https://github.com/zhangsan/joker")[https://github.com/zhangsan/joker] \
- 设计并实现了笑话分类算法,确保笑话生成器能准确地将笑话分为爆笑、冷笑和微笑三个级别,让用户在笑料丰富的同时能得到适合自己口味的笑话。
#h3[智能梦境] #h(0.3cm)#link("https://github.com/zhangsan/joker")[https://github.com/zhangsan/intelli-dream] \
- 通过深度学习算法和神经网络模型,我们能够分析用户的睡眠模式和脑电波,为他们提供个性化的梦境刺激,让他们在梦中体验奇幻、创意和冒险的旅程。
#section-title[个人技能]
- 拖延症高手:我擅长将任务推迟到最后一刻,然后以惊人的速度完成
- 熬夜能手:我具备超凡的熬夜能力,可以在没有咖啡因的情况下保持精力充沛
- 键盘快手:我可以用一只手快速打字,而且从不看屏幕 |
https://github.com/DaAlbrecht/thesis-TEKO | https://raw.githubusercontent.com/DaAlbrecht/thesis-TEKO/main/thesis.typ | typst | #import "template.typ": *
#import "metadata.typ": *
#import "@preview/tablex:0.0.5": tablex, cellx
#import "personal/Cover.typ" as cover
#show figure.where(kind: "appendix"): it => it.body
#let appendix = figure.with(kind: "appendix", numbering: "A", supplement: [Appendix])
#show link: underline
#show: project.with(
title: "Microservice for messaging-based replay function",
authors: (cover.author,),
abstract: include("content/Abstract.typ"),
date: "October 30, 2023",
school: cover.school,
degree: cover.degree,
class: cover.class,
)
= Executive summary
#include "./content/Executive_summary.typ"
= Glossary
#figure(tablex(
columns: (auto, 1fr),
rows: (auto),
align: (center, left),
[*Terminology*],
[*Description*],
[OCI],
[Open Container Initiative],
[AMQP],
[Advanced Message Queuing Protocol],
[TCP],
[Transmission Control Protocol],
[FIFO],
[First In First Out],
[CI],
[Continuous Integration],
[CD],
[Continuous Delivery],
[iff],
[if and only if],
[ELK-Stack],
[Elasticsearch, Logstash, Kibana],
[COTS],
[Commercial Off-The-Shelf],
), kind: table, caption: "Glossary")<glossary>
#pagebreak()
= Curriculum vitae
#include "personal/cv.typ"
= Introduction
#include "./content/Introduction.typ"
= Task analysis
#include "./content/task_analysis.typ"
= Use cases<Use_cases>
#include "./content/Use_cases.typ"
= Project plan
#include "./content/Projectplan.typ"
= Requirements
#include "./content/Requirements.typ"
= Research
#include "./content/Research.typ"
= Evaluation<evaluation>
#include "./content/Evaluation.typ"
= Implementation
#include "./content/Implementation.typ"
= Verification
#include "./content/Verification.typ"
= Configuration management
#include "./content/Configuration_management.typ"
= Conclusion
#include "./personal/Conclusion.typ"
= Closing remarks
#include "./personal/Closing_remarks.typ"
= Acknowledgement
#include "./personal/Acknowledgement.typ"
= Statement of authorship
Work that is demonstrably taken over in full or in the essential parts unchanged
or without correct reference to the source is considered prefabricated and will
not be evaluated.
#text(weight: "bold")[I confirm that I have written this thesis independently and have marked all sources used. This thesis has not already been submitted to an examination committee in the same or a similar form.]
#linebreak()
Name / First name:
#for i in range(5) {
linebreak()
}
Place / Date / Signature:
#pagebreak(weak: true)
#set par(linebreaks: "simple")
#show bibliography: it => {
set heading(outlined: false)
show heading: it => [
#underline(smallcaps(it.body), evade: true, offset: 4pt)
#v(12pt)
]
it
}
#bibliography("./references.bib", style: "ieee")
|
|
https://github.com/dismint/docmint | https://raw.githubusercontent.com/dismint/docmint/main/multicore/lec3.typ | typst | #import "template.typ": *
#show: template.with(
title: "Lecture 3",
subtitle: "6.5081"
)
= Queues
== 2 Thread Lock-Based Queue
The idea is to have a circular queue (stored as a list) where the head and tail pointers dance around in a circle.
- To enqueue, we increase the tail counter and add the element
- To dequeue, we increase the head counter and remove the element
To ensure everything is atomic, all operations are locked.
== Wait-Free 2 Thread Lock-Based Queue
Assume that one thread will only *enqueue* and the other will only *dequeue*. It's very clear why the above implementation was correct - how do we show that this one is also correct?
Thus we need to find a way to specify a concurrent queue object, and also a way to prove that an algorithm that attempts to implement this specification is sound.
= Defining Concurrent Objects
We need to specify both the safety and liveness property:
+ When an implementation is *correct*.
+ The condition under which it guarantees progress.
== Sequential Specifications
Recall the definition of *preconditions* and *postconditions*.
#example(
title: "Pre/Postconditions for Dequeue"
)[
/ Precondition: Queue is empty.
/ Postcondition: Returns and removes the first item in queue.
]
=== Benefits of Sequential Specifications
- Interactions among methods are captured by side effects on the object state.
- Documentation size scales linearly in the number of methods.
- Can add new methods without changing the specification of old methods.
== Concurrent Specifications
The main difference between concurrent and sequential methods is the fact that there is a notion of *time* in concurrent methods. Rather than being an *event*, a concurrent method is an *interval*.
/ Sequential: Objects only need meaningful states between method calls.
/ Concurrent: Because of overlapping method calls, "between" may never exist.
Thus as compared to sequential method specifications, we need to characterize *all* possible interactions, including the interleaving of different methods.
This means that when we add a concurrent method, we can't add documentation independently of other methods.
In a lock based approach, despite methods heavily overlapping, there is a way to get an ordering of events that don't overlap, where the critical operations occur. Thus to avoid all these problems mentioned above, we want to try and figure out a way to map concurrent method to sequential methods.
#define(
title: "Linearizability"
)[
Each method should "take effect" instantaneously between invocation and response events.
An object is considered linearizable if all possible executions are linearizable.
]
Because the linearization point depends on execution, we need to describe the point in context of an execution.
Let us split method calls into two events.
#define(
title: "Invocation Notation"
)[
#align(center)[`A q.enq(x)`]
]
#define(
title: "Response Notation"
)[
#align(center)[`A q: void`]
]
An invocation and response match if the thread and object names agree, and thus correspond to a method call.
We can view this history in terms of *projections*, such as an object or thread projection. We essentially filter the history for just these involved parties.
An invocation is pending if it has no matching response.
#define(
title: "Sequential Histories"
)[
A history is sequential if method calls of different threads to do not interleave.
]
#define(
title: "Well-Formed Concurrent History"
)[
If the thread projections are sequential, then it is concurrently well-formed. This can be seen as a weaker form of the above definition.
]
#define(
title: "Equivalent Histories"
)[
If the thread projections are the same for every thread, then the two executions are *equal*, even if the interleaving of the operations was different.
]
== Linearizability
How do we actually tell something is linearizable? History $bold(H)$ can be considered linearizable if it can be extended to another history $bold(G)$ by:
- Appending zero more more responses to pending invocations
- Discarding other pending invocations
#twocol(
[
The end result should be a legal sequential history where all orderings in $bold(G)$ fall under a subset of some legal sequential history $bold(S)$
],
[temp]
// bimg("img/subset.png")
)
|
|
https://github.com/university-makino/Microcomputer-control-and-exercises | https://raw.githubusercontent.com/university-makino/Microcomputer-control-and-exercises/master/report/プレレポート1/report.typ | typst | //フォント設定//
#let gothic = "Hiragino Kaku Gothic Pro"
//本文フォント//
#set text(11pt, font: gothic, lang: "ja")
//タイトル・見出しフォント//
#set heading(numbering: "1.1")
#let heading_font(body) = {
show regex("[\p{scx: Han}\p{scx: Hira}\p{scx: Kana}]"): set text(font: gothic)
body
}
#show heading: heading_font
//タイトルページここから//
#align(right, text()[
#text[提出日]#datetime.today().display("[year]年[month]月[day]日")
])
#v(150pt)
#align(center, text(30pt)[
#heading_font[*プレ・レポート1*]
])
// #align(center, text(14pt)[
// #heading_font[*サブタイトル*]
// ])
#v(1fr)
#align(right)[
#table(
columns:(auto, auto),
align: (right, left),
stroke: none,
[講義名],[マイコン制御および演習],
[担当教員],[伊藤 暢浩先生],
[],[],
[学籍番号],[k22120],
[所属],[情報科学部 情報科学科],
[学年],[3年],
[氏名],[牧野遥斗]
)
]
#pagebreak()
//本文ここから//
= チュートリアル
== 以下の用語を調べなさい
=== アナログ
アナログは、連続した量を他の連続した量で表示すること。デジタルが連続量を離散的な数値として表現(標本化・量子化)することと対比される@analog_wikipedia 。
=== デジタル
デジタルとは、量を段階的に区切って数字で表すことや、情報を離散的な値つまり飛び飛びの値のあつまりとして表現し"段階的な "物理量に対応させて記憶・伝送する方式や、データを "有限桁の数値" で表現する方法であり、たとえば 0と1だけを有限個使って情報を伝えることである@digital_wikipedia 。
=== センサ
センサは、自然現象や人工物の機械的・電磁気的・熱的・音響的・化学的性質あるいはそれらで示される空間情報・時間情報を、何らかの科学的原理を応用して、人間や機械が扱い易い別媒体の信号に置き換える装置のことをいう@sensor_wikipedia 。
=== アクチュエータ
電気・空気圧・油圧などのエネルギーを機械的な動きに変換し、機器を正確に動かす駆動装置@actuator 。
=== LED, 極性
ダイオードの1種で、順方向に電圧を加えた際に発光する半導体素子である。発光原理にはエレクトロルミネセンス効果を利用している@led_wikipedia 。
LEDには極性があり、アノード(+)とカソード(-)がある。アノードに正の電圧を加えると発光する。
見分け方は、アノードには長い足がついている。また、LEDが平らな場合は、平らな側がカソードである。
=== 回路図,実体配線図
回路図とは、電気回路や空気圧機器、油圧機器などの回路を記載する図を指す@circuit_diagram 。
実体配線図とは、実物に近いように部品をかき,配線の様子を線で結むすんで書いた回路図の一種。
@CircuitDiagramAndWiringDiagram では、回路図と実体配線図の比較を示している。
#figure(
image("./img/配線図と実体配線図.png",width: 50%),
caption: "回路図と実体配線図"
)<CircuitDiagramAndWiringDiagram>
=== ブレッドボード
「ブレッドボード」とは、簡単に組み立てられる回路基板である。
はんだ付けが不要で部品やリード線を差すだけで回路が組み立てられる。
部品エリアは縦に6ピンずつ連結。電源ラインは横方向に連結されている。
@BulletBoard では、ブレッドボードの構造を示す。
#figure(
image("./img/BulletBoard.png",width: 50%),
caption: "ブレッドボードの構造"
)<BulletBoard>
=== カラーコード(抵抗)
抵抗器にはその抵抗値や許容差などを表すマーキングが印刷されており、
その表示方法、内容、読み方はメーカー、製品、サイズなどにより個別のルールがある。
カラーコードは小さい部品でも印刷をすることができ、抵抗値を確認することができる。
読み方は、抵抗器の色の順番によって抵抗値を読み取る。
黒は0、茶色は1、赤は2、オレンジは3、黄色は4、緑は5、青は6、紫は7、灰色は8、白は9である。
@ColorCode では、カラーコードの読み方を示している。
#figure(
image("./img/ColorCode.png",width: 50%),
caption: "カラーコードの読み方"
)<ColorCode>
=== プルダウン・プルアップ(抵抗)
プルアップ(プルダウン)抵抗とは、電子回路における「浮いている」状態を避けるための抵抗である。マイコンの入力端子は、必ず電圧源、グランド、グランド基準信号源に接続しなければならず「浮いている」状態を極力避けるようにするため。
5Vもしくは、GNDに接続されていないと、ノイズに弱くなり誤作動を起こすことがある。
== 以下のカラーコードを見て抵抗値を答えよ
+ 橙橙茶金 = 330 Ω ± 5%
+ 白茶赤金 = 9100 Ω ± 5%
+ 青灰茶金 = 680 Ω ± 5%
+ 茶黒茶金 = 100 Ω ± 5%
+ 橙灰橙金 = 38k Ω ± 5%
+ 緑黒黒金 = 50 Ω ± 5%
+ 茶白茶金 = 190 Ω ± 5%
+ 橙茶黄金 = 310k Ω ± 5%
== 以下の抵抗値を見てカラーコードを答えよ.ただし,許容差はいずれも± 5 %とする.
+ 10k Ω = 茶黒橙金
+ 180 Ω = 茶灰茶金
+ 330 Ω = 橙橙茶金
+ 680 Ω = 青灰茶金
+ 470 Ω = 黄紫茶金
+ 100 Ω = 茶黒茶金
+ 1k Ω = 茶黒赤金
+ 79 Ω = 紫白黒金
= プレ・レポート(課題 1)
== この電子部品 (Cds セル 5 φ,@CdsCell ) を次のような点から調べなさい。
#figure(
image("./img/Cds.png",width: 50%),
caption: "Cds セル"
)<CdsCell>
=== どのような部品か
CdS(硫化カドミウム)を使用した光センサーで、光の強さに応じて電気抵抗が低下する抵抗器である。 人の目の特性に近い特性(緑色の光に対して高感度)を持っているため、各種明るさセンサーに最適である。
=== どのような仕組みか
CdSセルは、カドミウムと硫黄の化合物である。
カドミウム(Cd)は毒性のある重金属で最外殻の電子は原子核との結合が弱く、自由電子となり導電性である。
これに硫黄(S)を結合させるとカドミウムの自由電子を硫黄原子が捕捉して絶縁体に変化する。
この自由電子の捕捉力は非常に弱く、光があたると自由電子を放出して導体に変化する。
したがって、光の量によって放出する自由電子の量が変化し、抵抗値が変化することになる。
これを「内部光電効果」と呼ぶ。
=== どのような入力を取り扱うのか
GL5528では、受講部に入る光の量、照度(Lux) を入力として取り扱う。
=== 入力に応じて出力がどう変化するのか (データシートや仕様書を参考に)
GL5528では、暗い時は約1MΩ、明るい時は約10~20kΩの抵抗値を持つ。
グラフは比例関係になっており、照度が高いほど抵抗値が低くなる。
@CdsGraph では、Cdsセルの照度による抵抗値の変化を示している。
#figure(
image("./img/CdsGraph.png",width: 50%),
caption: "Cds グラフ"
)<CdsGraph>
=== どのようなピンアサイン (各ピンの役割) か
特に抵抗のように動作をするためピンアサインなどはないが、@CdsStructure 構造図を示すと、2つの端子があることがわかる。
#figure(
image("./img/CdsStructure.png",width: 50%),
caption: "Cds 構造"
)<CdsStructure>
=== 正しい動作の条件,範囲は何か
+ ピーク波長: 540nm
+ 最大電圧: 150VDC
+ 最大電力: 100mW
+ 明抵抗: 10k~20kS2(10Lux時)
+ 暗抵抗: 1MΩ
+ 反応時間: 上昇時間 20ms、下降時間 30ms
== センサ類を扱う上で「抵抗分圧」という用語が重要である。この用語について調べ、図と数式を使用しプレ・レポートにまとめなさい。また、@ResistorDivider のR2を変化させた場合、どのような動作をするかまとめなさい。
#figure(
image("./img/PullUp.png",width: 50%),
caption: "抵抗分圧"
)<ResistorDivider>
抵抗分圧とは、電圧を分圧するために抵抗を使用することである。
抵抗分圧回路は、2つの抵抗を直列に接続し、その間に電圧をかけることで、電圧を分圧することができる。
抵抗分圧回路の出力電圧は、次の式で計算できる。
```
Vout = Vin * (R2 / (R1 + R2))
```
R2を変化させると、抵抗値が変化するため、出力電圧も変化する。
R2を大きくすると、出力電圧は小さくなり、R2を小さくすると、出力電圧は大きくなる。
// bibファイルの指定 //
#bibliography("./bibliography.bib")
|
|
https://github.com/The-Notebookinator/notebookinator | https://raw.githubusercontent.com/The-Notebookinator/notebookinator/main/gallery/radial.typ | typst | The Unlicense | #import "/lib.typ": *
#import themes.radial: radial-theme, components, colors
#import colors: *
#show: notebook.with(
theme: radial-theme,
team-name: "53E",
season: "Over Under",
)
#create-frontmatter-entry(
title: "test",
type: "decide",
date: datetime(year: 2024, month: 1, day: 1),
)[
#components.toc()
]
#create-body-entry(
title: "Title",
type: "decide",
date: datetime(year: 2024, month: 1, day: 1),
)[
= Heading
#lorem(20)
#grid(
columns: (1fr, 1fr),
gutter: 20pt,
lorem(40),
components.pie-chart(
(value: 8, color: green, name: "wins"),
(value: 2, color: red, name: "losses"),
),
)
#lorem(23)
= Heading
#lorem(40)
#components.decision-matrix(
properties: (
(name: "property 1", weight: 2),
(name: "property 2", weight: 0.5),
(name: "property 3", weight: 0.33),
(name: "property 4", weight: 0.01),
),
("choice 1", 5, 2, 3, 4),
("choice 2", 1, 2, 3, 1),
("choice 3", 1, 3, 3, 2),
("choice 4", 1, 2, 3, 5),
("choice 5", 1, 2, 3, 1),
)
#lorem(20)
#components.admonition(type: "decision")[#lorem(20)]
= Heading
```cpp
#include <iostream>
int main() {
printf("hello world\n")
return 0;
}
```
]
#create-body-entry(
title: "Title",
type: "test",
date: datetime(year: 2024, month: 1, day: 1),
)[
= Heading
#lorem(20)
#components.admonition(type: "note")[#lorem(50)]
= Heading
#lorem(20)
#components.plot(
title: "My Epic Graph",
(name: "thing 1", data: ((1, 2), (2, 5), (3, 5))),
(name: "thing 2", data: ((1, 1), (2, 7), (3, 6))),
(name: "thing 3", data: ((1, 1), (2, 3), (3, 8))),
)
#grid(
columns: (1fr, 1fr),
gutter: 20pt,
components.admonition(type: "warning")[#lorem(20)],
lorem(20),
)
]
#create-body-entry(
title: "Title",
type: "management",
date: datetime(year: 2024, month: 1, day: 1),
)[
= Heading
#lorem(50)
#align(
center,
components.pie-chart(
(value: 2985, color: yellow, name: "Competitions"),
(value: 3000, color: blue, name: "Travel"),
(value: 2400, color: red, name: "Materials"),
),
)
#lorem(50)
= Heading
#components.gantt-chart(
start: datetime(year: 2024, month: 1, day: 27),
end: datetime(year: 2024, month: 2, day: 3),
tasks: (
("Build Robot", (0, 4)),
("Code Robot", (3, 6)),
("Drive Robot", (5, 7)),
("Destroy Robot", (7, 8)),
),
goals: (("Tournament", 4),),
)
#lorem(40)
#components.admonition(type: "example")[#lorem(50)]
]
|
https://github.com/typst-doc-cn/tutorial | https://raw.githubusercontent.com/typst-doc-cn/tutorial/main/src/basic/reference-utils.typ | typst | Apache License 2.0 | #import "mod.typ": *
#import "/typ/typst-meta/docs.typ": typst-v11
#import "@preview/cmarker:0.1.0": render as md
#show: book.page.with(title: [参考:函数表(字典序)])
#let table-lnk(name, ref, it, scope: (:), res: none, ..args) = (
align(center + horizon, link("todo", name)),
it,
align(horizon, {
set heading(bookmarked: false, outlined: false)
eval(it.text, mode: "markup", scope: scope)
}),
)
#let table-item(c, mp, featured) = {
let item = mp.at(c)
(typst-func(c), item.title, ..featured(item))
}
#let table-items(mp, featured) = mp.keys().sorted().map(
it => table-item(it, mp, featured)).flatten()
#let featured-func(item) = {
return (md(item.body.content.oneliner), )
}
#let featured-scope-item(item) = {
return (md(item.oneliner), )
}
== 分类:函数
#table(
columns: (1fr, 1fr, 2fr),
[函数], [名称], [描述],
..table-items(typst-v11.funcs, featured-func)
)
== 分类:方法
#table(
columns: (1fr, 1fr, 2fr),
[方法], [名称], [描述],
..table-items(typst-v11.scoped-items, featured-scope-item)
)
|
https://github.com/liamaxelrod/Resume | https://raw.githubusercontent.com/liamaxelrod/Resume/main/resume%202/cv.typ | typst | // Imports
#import "@preview/brilliant-cv:2.0.2": cv
#let metadata = yaml("./metadata.yml")
#let importModules(modules, lang: metadata.language) = {
for module in modules {
include "content/" + module + ".typ"
}
}
#show: cv.with(
metadata,
profilePhoto: image("./src/avatar.jpg")
)
#importModules((
"education",
"professional",
"projects",
// "certificates",
// "publications",
"skills",
))
|
|
https://github.com/CL4R3T/GroupTheory-I-_homework | https://raw.githubusercontent.com/CL4R3T/GroupTheory-I-_homework/main/requirements.typ | typst | #import "@preview/problemst:0.1.0": * |
|
https://github.com/sitandr/typst-examples-book | https://raw.githubusercontent.com/sitandr/typst-examples-book/main/src/basics/scripting/types_2.md | markdown | MIT License | # Types, part II
In Typst, most of things are **immutable**. You can't change content, you can just create new using this one (for example, using addition).
Immutability is very important for Typst since it tries to be _as pure language as possible_. Functions do nothing outside of returning some value.
However, purity is partly "broken" by these types. They are *super-useful* and not adding them would make Typst much pain.
However, using them adds complexity.
## Arrays (`array`)
> [Link to Reference](https://typst.app/docs/reference/foundations/array/).
Mutable object that stores data with their indices.
### Working with indices
```typ
#let values = (1, 7, 4, -3, 2)
// take value at index 0
#values.at(0) \
// set value at 0 to 3
#(values.at(0) = 3)
// negative index => start from the back
#values.at(-1) \
// add index of something that is even
#values.find(calc.even)
```
### Iterating methods
```typ
#let values = (1, 7, 4, -3, 2)
// leave only what is odd
#values.filter(calc.odd) \
// create new list of absolute values of list values
#values.map(calc.abs) \
// reverse
#values.rev() \
// convert array of arrays to flat array
#(1, (2, 3)).flatten() \
// join array of string to string
#(("A", "B", "C")
.join(", ", last: " and "))
```
### List operations
```typ
// sum of lists:
#((1, 2, 3) + (4, 5, 6))
// list product:
#((1, 2, 3) * 4)
```
### Empty list
```typ
#() \ // this is an empty list
#(1,) \ // this is a list with one element
BAD: #(1) // this is just an element, not a list!
```
## Dictionaries (`dict`)
> [Link to Reference](https://typst.app/docs/reference/foundations/dictionary/).
Dictionaries are objects that store a string "key" and a value, associated with that key.
```typ
#let dict = (
name: "Typst",
born: 2019,
)
#dict.name \
#(dict.launch = 20)
#dict.len() \
#dict.keys() \
#dict.values() \
#dict.at("born") \
#dict.insert("city", "Berlin ")
#("name" in dict)
```
### Empty dictionary
```typ
This is an empty list: #() \
This is an empty dict: #(:)
```
|
https://github.com/matetamasi/Medve-Automata-9 | https://raw.githubusercontent.com/matetamasi/Medve-Automata-9/master/jegyzet.typ | typst | #import "@preview/finite:0.3.0": automaton, layout
#let aut = ( ..it,) => {
show "Start":""
automaton(..it)
}
#let maut = (..it, style: (:), radius: 0.45, curve: 0) => {
show "Start":""
style.insert("transition", (curve: curve, label: (dist: 0.25)))
style.insert("state", (radius: radius))
automaton(..it, style: style)
}
#let parallel-layout = layout.custom.with(
positions: (ctx, radii, states) => {
let xinc = 1.5
let x = xinc
let pos = (:)
let toprow = true
let h = 1
for (name, r) in radii {
if (name == "S") {
pos.insert(name, (0,0))
}
else {
pos.insert(name, (x, if(toprow){h}else{-h}))
if (toprow) {toprow = false;} else {toprow = true; x += xinc}
}
}
return pos
}
)
#let trap-layout = layout.custom.with(
positions: (ctx, radii, states) => {
let xinc = 1.5
let x = xinc
let pos = (:)
for (name, r) in radii {
if (name == "N") {
pos.insert(name, (x/2, -1.7))
}
else {
pos.insert(name, (x, 0))
x += xinc
}
}
return pos
}
)
#let subtasks(list) = {
let keylist = list.enumerate()
set enum(numbering: "a)")
align(center, {
grid(
columns: 2,
row-gutter: 0.4cm,
column-gutter: 0.1cm,
align: left,
..keylist.map(a => enum.item(a.at(0)+1, a.at(1)))
)
})
}
#let important = text.with(red)
= 1. Foglalkozás
== Téma bevezetése:
- Programozás?
- Algoritmusok?
- Állapotgépek?
DVA intuitívan - egy gép, ami betűket olvas, és észben tartja, hogy hol tart, a végén pedig eldönti, hogy a szót elfogadja, vagy sem.
== Fogalmak:
- Betű - Egy darab (szétválaszthatatlan) karakter.
- Ábécé - betűk halmaza. ($Sigma$)
- Szó - Betűk egymásutánja.
- Nyelv - Szavak halmaza.
- $a^n$ $a$ betű $n$-szer egymás után leírva, ahol $a in Sigma, n in NN$
== Jelölések:
#aut((
S: (A:0, S:1),
A: (A:0, B:1),
B: (B:"0,1"),
),
style: (
transition: (curve: 0)
)
)
- Állapot - Nagy (latin) betű.
- Átmenet - Állapotok közti nyíl
- Elfogadó állapot - <NAME>
- $epsilon$ - üres szó
- minden állapotból kell átmenet az ábécé minden betűjére
- minden állapotból minden betű csak egyszer
#important[- szóvá kell tenni, hogy ez a DVA, lesz más is, ahol kicsit mások a szabályok]
== Közös feladatmegoldás
== Önálló feladatmegoldás
= 2. Foglalkozás
== Hiányos DVA
- elhagyhatók átmenetek
- nem definiált átmenet esetén azonnal elutasít
#important[- feladatokon keresztül vegyék észre, hogy ez is egy DVA-vá átalakítható]
== Feladatok
== NVA
- egy állapotban egy betűre több átmenet definiálható
- ha van egy megfelelő lefutás, akkor a szót elfogadjuk
- általában hiányos is (hogy kevesebbet kelljen írni)
== Feladatok
== NVA és DVA ekvivalens
- szerintük melyik az "erősebb?"
- mutassuk meg, hogy NVA alakítható DVA-vá
- vegyük észre, hogy a DVA egy NVA
= 3. Folgalkozás
== "Verseny"
(Ezt nem én találtam ki, de a tematika tanításakor népszerű szokott lenni)
- Gyerekek rendeződjenek 4-5 fős csapatokba
- Miden csapat találjon ki egy automatát annyi állapottal, ahányan vannak
- Szimulálják az automatát
- A többi csapat adjon inputokat, és próbálja meg kitalálni, hogy milyen automatát szimulálnak
= 4. Folglalkozás
== Nem mindent lehet NVA-val kifejezni
- példanyelv, amire nem tudnak automatát adni
- veremautomaták bevezetése
- közös feladatmegoldás
#pagebreak(weak: true)
= Feladatsor megoldásokkal
Ahol a feladat mást nem mond, az ábécé legyen $Sigma = {a, b}$.
+ Adj meg egy determinisztikus véges automatát, mely azokat a szavakat fogadja el, amelyekben szerpel legalább 3 darab $a$ betű.
#maut((
S: (S: "a", A: "b"),
A: (A: "a", B: "b"),
B: (B: "a", C: "b"),
C: (C: "a,b")
),
)
+ Adj determinisztikus véges automatát a következő nyelvekre:
#subtasks((
[2 betűből álló szavak
#maut(
(
S: (A: "a,b"),
A: (B: "a,b"),
B: (C: "a,b"),
C: (C: "a,b"),
),
radius: 0.4,
final: "B",
)
],
[szavak, melyek első és utolsó betűje megegyezik
#maut(
(
S: (A0: "a", B0: "b"),
A0: (A0: "a", A1: "b"),
B0: (B0: "b", B1:"a"),
A1: (A0: "a", A1:"b"),
B1: (B0: "b", B1:"a"),
),
final: "SA0B0",
layout: parallel-layout,
curve: 0.35,
style: (S-B0: (curve: -.35)),
)
],
[szavak, melyekben minden \"a\" után \"bb\" következik
#maut(
(
S: (S: "b", A: "a"),
A: (B: "b", N: "a"),
B: (S: "b", N: "a"),
N: (N: "a,b"),
),
layout: trap-layout,
final: "S",
style: (
B-S: (curve: -.85),
B-N: (label: (pos: 0.7)),
S-S: (curve: .5, anchor: bottom),
A-N: (label: (angle: 0deg, pos: 0.45)),
N-N: (curve: .5, anchor: left),
),
)
],
[szavak, melyekben a \"aa\" részszó pontosan egyszer szerepel
#maut(
(
S: (A: "a", S: "b"),
A: (S: "b", B: "a"),
B: (C: "b", N: "a"),
C: (C: "b", D: "a"),
D: (C: "b", N: "a"),
N: (N: "a,b")
),
final: "BCD",
curve: .7,
style: (
A-S: (curve: .35),
S-A: (curve: .35),
B-N: (curve: -1.80),
C-C: (anchor: bottom, curve: .4)
),
)
]
))
|
|
https://github.com/TypstApp-team/typst | https://raw.githubusercontent.com/TypstApp-team/typst/master/tests/typ/compiler/string.typ | typst | Apache License 2.0 | // Test the string methods.
// Ref: false
---
// Test the `len` method.
#test("Hello World!".len(), 12)
---
// Test the `first` and `last` methods.
#test("Hello".first(), "H")
#test("Hello".last(), "o")
#test("🏳️🌈A🏳️⚧️".first(), "🏳️🌈")
#test("🏳️🌈A🏳️⚧️".last(), "🏳️⚧️")
---
// Error: 2-12 string is empty
#"".first()
---
// Error: 2-11 string is empty
#"".last()
---
// Test the `at` method.
#test("Hello".at(1), "e")
#test("Hello".at(4), "o")
#test("Hello".at(-1), "o")
#test("Hello".at(-2), "l")
#test("Hey: 🏳️🌈 there!".at(5), "🏳️🌈")
---
// Test `at`'s 'default' parameter.
#test("z", "Hello".at(5, default: "z"))
---
// Error: 2-14 string index 2 is not a character boundary
#"🏳️🌈".at(2)
---
// Error: 2-15 no default value was specified and string index out of bounds (index: 5, len: 5)
#"Hello".at(5)
---
#test("Hello".at(5, default: (a: 10)), (a: 10))
---
// Test the `slice` method.
#test("abc".slice(1, 2), "b")
#test("abc🏡def".slice(2, 7), "c🏡")
#test("abc🏡def".slice(2, -2), "c🏡d")
#test("abc🏡def".slice(-3, -1), "de")
---
// Error: 2-21 string index -1 is not a character boundary
#"🏳️🌈".slice(0, -1)
---
// Test the `clusters` and `codepoints` methods.
#test("abc".clusters(), ("a", "b", "c"))
#test("abc".clusters(), ("a", "b", "c"))
#test("🏳️🌈!".clusters(), ("🏳️🌈", "!"))
#test("🏳️🌈!".codepoints(), ("🏳", "\u{fe0f}", "\u{200d}", "🌈", "!"))
---
// Test the `contains` method.
#test("abc".contains("b"), true)
#test("b" in "abc", true)
#test("1234f".contains(regex("\d")), true)
#test(regex("\d") in "1234f", true)
#test("abc".contains("d"), false)
#test("1234g" in "1234f", false)
#test("abc".contains(regex("^[abc]$")), false)
#test("abc".contains(regex("^[abc]+$")), true)
---
// Test the `starts-with` and `ends-with` methods.
#test("Typst".starts-with("Ty"), true)
#test("Typst".starts-with(regex("[Tt]ys")), false)
#test("Typst".starts-with("st"), false)
#test("Typst".ends-with("st"), true)
#test("Typst".ends-with(regex("\d*")), true)
#test("Typst".ends-with(regex("\d+")), false)
#test("Typ12".ends-with(regex("\d+")), true)
#test("typst13".ends-with(regex("1[0-9]")), true)
#test("typst113".ends-with(regex("1[0-9]")), true)
#test("typst23".ends-with(regex("1[0-9]")), false)
---
// Test the `find` and `position` methods.
#let date = regex("\d{2}:\d{2}")
#test("Hello World".find("World"), "World")
#test("Hello World".position("World"), 6)
#test("It's 12:13 now".find(date), "12:13")
#test("It's 12:13 now".position(date), 5)
---
// Test the `match` method.
#test("Is there a".match("for this?"), none)
#test(
"The time of my life.".match(regex("[mit]+e")),
(start: 4, end: 8, text: "time", captures: ()),
)
// Test the `matches` method.
#test("Hello there".matches("\d"), ())
#test("Day by Day.".matches("Day"), (
(start: 0, end: 3, text: "Day", captures: ()),
(start: 7, end: 10, text: "Day", captures: ()),
))
// Compute the sum of all timestamps in the text.
#let timesum(text) = {
let time = 0
for match in text.matches(regex("(\d+):(\d+)")) {
let caps = match.captures
time += 60 * int(caps.at(0)) + int(caps.at(1))
}
str(int(time / 60)) + ":" + str(calc.rem(time, 60))
}
#test(timesum(""), "0:0")
#test(timesum("2:70"), "3:10")
#test(timesum("1:20, 2:10, 0:40"), "4:10")
---
// Test the `replace` method with `Str` replacements.
#test("ABC".replace("", "-"), "-A-B-C-")
#test("Ok".replace("Ok", "Nope", count: 0), "Ok")
#test("to add?".replace("", "How ", count: 1), "How to add?")
#test("AB C DEF GH J".replace(" ", ",", count: 2), "AB,C,DEF GH J")
#test("Walcemo"
.replace("o", "k")
.replace("e", "o")
.replace("k", "e")
.replace("a", "e"),
"Welcome"
)
#test("123".replace(regex("\d$"), "_"), "12_")
#test("123".replace(regex("\d{1,2}$"), "__"), "1__")
---
// Test the `replace` method with `Func` replacements.
#test("abc".replace(regex("[a-z]"), m => {
str(m.start) + m.text + str(m.end)
}), "0a11b22c3")
#test("abcd, efgh".replace(regex("\w+"), m => {
upper(m.text)
}), "ABCD, EFGH")
#test("hello : world".replace(regex("^(.+)\s*(:)\s*(.+)$"), m => {
upper(m.captures.at(0)) + m.captures.at(1) + " " + upper(m.captures.at(2))
}), "HELLO : WORLD")
#test("hello world, lorem ipsum".replace(regex("(\w+) (\w+)"), m => {
m.captures.at(1) + " " + m.captures.at(0)
}), "world hello, ipsum lorem")
#test("hello world, lorem ipsum".replace(regex("(\w+) (\w+)"), count: 1, m => {
m.captures.at(1) + " " + m.captures.at(0)
}), "world hello, lorem ipsum")
#test("123 456".replace(regex("[a-z]+"), "a"), "123 456")
#test("abc".replace("", m => "-"), "-a-b-c-")
#test("abc".replace("", m => "-", count: 1), "-abc")
#test("123".replace("abc", m => ""), "123")
#test("123".replace("abc", m => "", count: 2), "123")
#test("a123b123c".replace("123", m => {
str(m.start) + "-" + str(m.end)
}), "a1-4b5-8c")
#test("halla warld".replace("a", m => {
if m.start == 1 { "e" }
else if m.start == 4 or m.start == 7 { "o" }
}), "hello world")
#test("aaa".replace("a", m => str(m.captures.len())), "000")
---
// Error: 23-24 expected string, found integer
#"123".replace("123", m => 1)
---
// Error: 23-32 expected string or function, found array
#"123".replace("123", (1, 2, 3))
---
// Test the `trim` method.
#let str = "Typst, LaTeX, Word, InDesign"
#let array = ("Typst", "LaTeX", "Word", "InDesign")
#test(str.split(",").map(s => s.trim()), array)
#test("".trim(), "")
#test(" abc ".trim(at: start), "abc ")
#test(" abc ".trim(at: end, repeat: true), " abc")
#test(" abc".trim(at: start, repeat: false), "abc")
#test("aabcaa".trim("a", repeat: false), "abca")
#test("aabca".trim("a", at: start), "bca")
#test("aabcaa".trim("a", at: end, repeat: false), "aabca")
#test("".trim(regex(".")), "")
#test("123abc456".trim(regex("\d")), "abc")
#test("123abc456".trim(regex("\d"), repeat: false), "23abc45")
#test("123a4b5c678".trim(regex("\d"), repeat: true), "a4b5c")
#test("123a4b5c678".trim(regex("\d"), repeat: false), "23a4b5c67")
#test("123abc456".trim(regex("\d"), at: start), "abc456")
#test("123abc456".trim(regex("\d"), at: end), "123abc")
#test("123abc456".trim(regex("\d+"), at: end, repeat: false), "123abc")
#test("123abc456".trim(regex("\d{1,2}$"), repeat: false), "123abc4")
#test("hello world".trim(regex(".")), "")
---
// Error: 17-21 expected either `start` or `end`
#"abc".trim(at: left)
---
// Test the `split` method.
#test("abc".split(""), ("", "a", "b", "c", ""))
#test("abc".split("b"), ("a", "c"))
#test("a123c".split(regex("\d")), ("a", "", "", "c"))
#test("a123c".split(regex("\d+")), ("a", "c"))
---
// Test the `rev` method.
#test("abc".rev(), "cba")
#test("ax̂e".rev(), "ex̂a")
---
// Error: 12-15 unknown variable: arg
#"abc".rev(arg)
---
// Error: 2-2:1 unclosed string
#"hello\"
|
https://github.com/TechnoElf/mqt-qcec-diff-thesis | https://raw.githubusercontent.com/TechnoElf/mqt-qcec-diff-thesis/main/content/implementation/benchmarking.typ | typst | == QCEC Benchmarking Tool
Besides testing the newly developed approaches for correctness, possible performance regressions should be monitored as well.
@qcec does not have built-in benchmarks, however.
For this purpose, a benchmarking tool was therefore developed to test different configurations of the equivalence checker on various circuit pairs.
This is necessary to show the quantitative improvement gained by using different application schemes.
Two different approaches were implemented, which will be discussed in the following sections.
=== Google Benchmark
The Google Benchmark framework was initially used to develop benchmarks for @mqt @qcec.
The benchmarks generally had the following procedure.
First, the equivalence checker was configured.
The application scheme was set to either the proportional or diff approach according to the benchmark definition.
Next, the circuits were loaded according to the benchmark definition.
Finally, the equivalence checking run was carried out in a loop by the benchmarking framework.
To generate the quantum circuits for the benchmark instances, @mqt Bench was used @quetschlich2023mqtbench.
A subset of the available benchmarks was chosen for initial tests, namely the Deutsch-Jozsa algorithm @deutsch1992quantum, Grover's algorithm @grover1996db and Shor's algorithm @shor1997discretelog.
The qubit count was set to 8 for initial testing.
These circuits were each compiled using Qiskit for the IBM native gate set and the IBM Eagle @qpu target device (called IBM Washington in @mqt Bench).
This @qpu has a total of 127 qubits and natively supports the $X$, square root of $x$, rotate $z$ and echoed cross-resonance gates @chow2021eagle.
Its gates are connected using a heavy-hexagonal layout.
While other @qpu[s] were not tested in this study, these should yield similar results as the compilation process works in the same manner on these platforms.
These benchmarks were manually downloaded from the @mqt Bench instance hosted by the Chair for Design Automation and subsequently implemented in the @qcec codebase.
This approach doesn't scale very well, however.
Each test instance takes roughly 30 lines of C++ code and the corresponding circuit must be downloaded by the user as there are too many circuits to reasonably add to the git repository.
Considering that @mqt Bench currently has 28 different quantum circuits, most of which have a variable number of qubits, this would be unreasonable to implement by hand @quetschlich2023mqtbench.
Furthermore, there are 36 permutations that can be compared for each benchmark instance as each level of specification and optimisation can be compared to all higher levels of specification and optimisation.
Additionally, it would certainly be interesting to test different combinations of compilers and targets in future work, which would be very difficult with this approach.
Another issue of Google Benchmark is the inability to benchmark variables other than runtime.
To benchmark @qcec, it is desirable to track and compare further variables.
For instance, the node count of the decision diagram can be a good indicator of the efficacy of the application scheme.
Due to these factors, it became necessary to implement a benchmarking framework specifically for @mqt @qcec.
=== MQT QCEC Bench
As Google Benchmark lacked the needed flexibility to adequately test @mqt @qcec, a new benchmarking wrapper around the tool was developed.
This framework was designed around a set of configuration files that specify how the equivalence checker is to be configured and which benchmark instances it should be run on.
The configuration of the equivalence checker currently only allows setting the application scheme for the alternating checker as this was sufficient for this work.
It can, however, trivially be extended to allow for a more flexible configuration.
The benchmark instance configuration allows specifying multiple instances, each with a name, an @mqt bench circuit, a choice of which optimisation and specification levels to compare, a qubit count, a minimum run count and a timeout after which the benchmark will abort.
These configuration files can be written by hand much more quickly than the Google Benchmark test cases.
Additionally, it was possible to script the creation of these configuration files using Python to allow programmatic generation of benchmark instances.
This approach was used to generate the final benchmark configuration with 190 instances.
Furthermore, unlike Google benchmark, this framework doesn't require manually downloading the circuits from @mqt Bench.
@qcec bench automatically builds the required files using the @mqt Bench python package if they haven't been built yet.
It also caches the results so future runs of the benchmark can be started more quickly.
Google Benchmark has a convenient feature to reduce the noise of measurements that was initially lacking from @qcec Bench.
When the runtime of the benchmark is very short, it will automatically increase the run count to calculate a more precise average.
This technique was also adopted in @qcec Bench as the variance for some of the smaller benchmark instances was too high to allow proper interpretation of the results.
|
|
https://github.com/MDLC01/board-n-pieces | https://raw.githubusercontent.com/MDLC01/board-n-pieces/main/src/chess-sym.typ | typst | MIT License | #let pawn = symbol(
("filled", "♟"),
("filled.r", "🨔"),
("filled.b", "🨩"),
("filled.l", "🨾"),
("stroked", "♙"),
("stroked.r", "🨎"),
("stroked.b", "🨣"),
("stroked.l", "🨸"),
("white", "♙"),
("white.r", "🨎"),
("white.b", "🨣"),
("white.l", "🨸"),
("black", "♟"),
("black.r", "🨔"),
("black.b", "🨩"),
("black.l", "🨾"),
("neutral", "🨅"),
("neutral.r", "🨚"),
("neutral.b", "🨯"),
("neutral.l", "🩄"),
)
#let knight = symbol(
("filled", "♞"),
("filled.r", "🨓"),
("filled.b", "🨨"),
("filled.l", "🨽"),
("filled.tr", "🨇"),
("filled.br", "🨜"),
("filled.bl", "🨱"),
("filled.tl", "🩆"),
("filled.bishop", "🩓"),
("filled.rook", "🩒"),
("filled.queen", "🩑"),
("stroked", "♘"),
("stroked.r", "🨍"),
("stroked.b", "🨢"),
("stroked.l", "🨷"),
("stroked.tr", "🨆"),
("stroked.br", "🨛"),
("stroked.bl", "🨰"),
("stroked.tl", "🩅"),
("stroked.bishop", "🩐"),
("stroked.rook", "🩏"),
("stroked.queen", "🩎"),
("white", "♘"),
("white.r", "🨍"),
("white.b", "🨢"),
("white.l", "🨷"),
("white.tr", "🨆"),
("white.br", "🨛"),
("white.bl", "🨰"),
("white.tl", "🩅"),
("white.bishop", "🩐"),
("white.rook", "🩏"),
("white.queen", "🩎"),
("black", "♞"),
("black.r", "🨓"),
("black.b", "🨨"),
("black.l", "🨽"),
("black.tr", "🨇"),
("black.br", "🨜"),
("black.bl", "🨱"),
("black.tl", "🩆"),
("black.bishop", "🩓"),
("black.rook", "🩒"),
("black.queen", "🩑"),
("neutral", "🨄"),
("neutral.r", "🨙"),
("neutral.b", "🨮"),
("neutral.l", "🩃"),
("neutral.tr", "🨈"),
("neutral.br", "🨝"),
("neutral.bl", "🨲"),
("neutral.tl", "🩇"),
)
#let bishop = symbol(
("filled", "♝"),
("filled.r", "🨒"),
("filled.b", "🨧"),
("filled.l", "🨼"),
("stroked", "♗"),
("stroked.r", "🨌"),
("stroked.b", "🨡"),
("stroked.l", "🨶"),
("white", "♗"),
("white.r", "🨌"),
("white.b", "🨡"),
("white.l", "🨶"),
("black", "♝"),
("black.r", "🨒"),
("black.b", "🨧"),
("black.l", "🨼"),
("neutral", "🨃"),
("neutral.r", "🨘"),
("neutral.b", "🨭"),
("neutral.l", "🩂"),
)
#let rook = symbol(
("filled", "♜"),
("filled.r", "🨑"),
("filled.b", "🨦"),
("filled.l", "🨻"),
("stroked", "♖"),
("stroked.r", "🨋"),
("stroked.b", "🨠"),
("stroked.l", "🨵"),
("white", "♖"),
("white.r", "🨋"),
("white.b", "🨠"),
("white.l", "🨵"),
("black", "♜"),
("black.r", "🨑"),
("black.b", "🨦"),
("black.l", "🨻"),
("neutral", "🨂"),
("neutral.r", "🨗"),
("neutral.b", "🨬"),
("neutral.l", "🩁"),
)
#let queen = symbol(
("filled", "♛"),
("filled.r", "🨐"),
("filled.b", "🨥"),
("filled.l", "🨺"),
("stroked", "♕"),
("stroked.r", "🨊"),
("stroked.b", "🨟"),
("stroked.l", "🨴"),
("white", "♕"),
("white.r", "🨊"),
("white.b", "🨟"),
("white.l", "🨴"),
("black", "♛"),
("black.r", "🨐"),
("black.b", "🨥"),
("black.l", "🨺"),
("neutral", "🨁"),
("neutral.r", "🨖"),
("neutral.b", "🨫"),
("neutral.l", "🩀"),
)
#let king = symbol(
("filled", "♚"),
("filled.r", "🨏"),
("filled.b", "🨤"),
("filled.l", "🨹"),
("stroked", "♔"),
("stroked.r", "🨉"),
("stroked.b", "🨞"),
("stroked.l", "🨳"),
("white", "♔"),
("white.r", "🨉"),
("white.b", "🨞"),
("white.l", "🨳"),
("black", "♚"),
("black.r", "🨏"),
("black.b", "🨤"),
("black.l", "🨹"),
("neutral", "🨀"),
("neutral.r", "🨕"),
("neutral.b", "🨪"),
("neutral.l", "🨿"),
)
#let equihopper = symbol(
("filled", "🩉"),
("filled.rot", "🩌"),
("stroked", "🩈"),
("stroked.rot", "🩋"),
("white", "🩈"),
("white.rot", "🩋"),
("black", "🩉"),
("black.rot", "🩌"),
("neutral", "🩊"),
("neutral.rot", "🩍"),
)
#let soldier = symbol(
("filled", "🩭"),
("stroked", "🩦"),
("red", "🩦"),
("black", "🩭"),
)
#let cannon = symbol(
("filled", "🩬"),
("stroked", "🩥"),
("red", "🩥"),
("black", "🩬"),
)
#let chariot = symbol(
("filled", "🩫"),
("stroked", "🩤"),
("red", "🩤"),
("black", "🩫"),
)
#let horse = symbol(
("filled", "🩪"),
("stroked", "🩣"),
("red", "🩣"),
("black", "🩪"),
)
#let elephant = symbol(
("filled", "🩩"),
("stroked", "🩢"),
("red", "🩢"),
("black", "🩩"),
)
#let mandarin = symbol(
("filled", "🩨"),
("stroked", "🩡"),
("red", "🩡"),
("black", "🩨"),
)
#let general = symbol(
("filled", "🩧"),
("stroked", "🩠"),
("red", "🩠"),
("black", "🩧"),
)
|
https://github.com/Myriad-Dreamin/typst.ts | https://raw.githubusercontent.com/Myriad-Dreamin/typst.ts/main/fuzzers/corpora/meta/footnote-refs_05.typ | typst | Apache License 2.0 |
#import "/contrib/templates/std-tests/preset.typ": *
#show: test-page
// Footnote call with label
#footnote(<fn>)
#footnote[Hi]<fn>
#ref(<fn>)
#footnote(<fn>)
|
https://github.com/typst/packages | https://raw.githubusercontent.com/typst/packages/main/packages/preview/unichar/0.1.0/ucd/block-100000.typ | typst | Apache License 2.0 | #let data = (
"0": ("<Plane 16 Private Use, First>", "Co", 0),
"fffd": ("<Plane 16 Private Use, Last>", "Co", 0),
)
|
https://github.com/frectonz/the-pg-book | https://raw.githubusercontent.com/frectonz/the-pg-book/main/book/172.%20ineq.html.typ | typst | ineq.html
Economic Inequality
January 2016Since the 1970s, economic inequality in the US has increased
dramatically. And in particular, the rich have gotten a lot richer.
Nearly everyone who writes about the topic says that economic inequality
should be decreased.I'm interested in this question because I was one of the founders of
a company called Y Combinator that helps people start startups.
Almost by definition, if a startup succeeds, its founders become
rich. Which means by helping startup founders I've been helping to
increase economic inequality. If economic inequality should be
decreased, I shouldn't be helping founders. No one should
be.But that doesn't sound right. What's going on here? What's going
on is that while economic inequality is a single measure (or more
precisely, two: variation in income, and variation in wealth), it
has multiple causes. Many of these causes are bad, like tax loopholes
and drug addiction. But some are good, like <NAME> and
<NAME> starting the company you use to find things online.If you want to understand economic inequality — and more importantly,
if you actually want to fix the bad aspects of it — you have to
tease apart the components. And yet the trend in nearly everything
written about the subject is to do the opposite: to squash together
all the aspects of economic inequality as if it were a single
phenomenon.Sometimes this is done for ideological reasons. Sometimes it's
because the writer only has very high-level data and so draws
conclusions from that, like the proverbial drunk who looks for his
keys under the lamppost, instead of where he dropped them, because the
light is better there. Sometimes it's because the writer doesn't
understand critical aspects of inequality, like the role of technology
in wealth creation. Much of the time, perhaps most of the time,
writing about economic inequality combines all three.___The most common mistake people make about economic inequality is
to treat it as a single phenomenon. The most naive version of which
is the one based on the pie fallacy: that the rich get rich by
taking money from the poor.Usually this is an assumption people start from rather than a
conclusion they arrive at by examining the evidence. Sometimes the
pie fallacy is stated explicitly:
...those at the top are grabbing an increasing fraction of the
nation's income — so much of a larger share that what's left over
for the rest is diminished....
[1]
Other times it's more unconscious. But the unconscious form is very
widespread. I think because we grow up in a world where the pie
fallacy is actually true. To kids, wealth is a fixed pie
that's shared out, and if one person gets more, it's at the expense
of another. It takes a conscious effort to remind oneself that the
real world doesn't work that way.In the real world you can create wealth as well as taking it from
others. A woodworker creates wealth. He makes a chair, and you
willingly give him money in return for it. A high-frequency trader
does not. He makes a dollar only when someone on the other end of
a trade loses a dollar.If the rich people in a society got that way by taking wealth from
the poor, then you have the degenerate case of economic inequality,
where the cause of poverty is the same as the cause of wealth. But
instances of inequality don't have to be instances of the degenerate
case. If one woodworker makes 5 chairs and another makes none, the
second woodworker will have less money, but not because anyone took
anything from him.Even people sophisticated enough to know about the pie fallacy are
led toward it by the custom of describing economic inequality as a
ratio of one quantile's income or wealth to another's. It's so
easy to slip from talking about income shifting from one quantile
to another, as a figure of speech, into believing that is literally
what's happening.Except in the degenerate case, economic inequality can't be described
by a ratio or even a curve. In the general case it consists of
multiple ways people become poor, and multiple ways people become
rich. Which means to understand economic inequality in a country,
you have to go find individual people who are poor or rich and
figure out why.
[2]If you want to understand change in economic inequality, you
should ask what those people would have done when it was different.
This is one way I know the rich aren't all getting richer simply
from some new system for transferring wealth to them from
everyone else. When you use the would-have method with startup
founders, you find what most would have done
back in 1960, when
economic inequality was lower, was to join big companies or become
professors. Before <NAME> started Facebook, his default
expectation was that he'd end up working at Microsoft. The reason
he and most other startup founders are richer than they would have
been in the mid 20th century is not because of some right turn the
country took during the Reagan administration, but because progress
in technology has made it much easier to start a new company that
grows fast.Traditional economists seem strangely averse to studying individual
humans. It seems to be a rule with them that everything has to start
with statistics. So they give you very precise numbers about
variation in wealth and income, then follow it with the most naive
speculation about the underlying causes.But while there are a lot of people who get rich through rent-seeking
of various forms, and a lot who get rich by playing zero-sum games,
there are also a significant number
who get rich by creating wealth. And creating wealth, as a source
of economic inequality, is different from taking it — not just
morally, but also practically, in the sense that it is harder to
eradicate. One reason is that variation in productivity is
accelerating. The rate at which individuals can create wealth
depends on the technology available to them, and that grows
exponentially. The other reason creating wealth is such a tenacious
source of inequality is that it can expand to accommodate a lot of
people.___I'm all for shutting down the crooked ways to get rich. But that
won't eliminate great variations in wealth, because as long as you leave
open the option of getting rich by creating wealth, people who want
to get rich will do that instead.Most people who get rich tend to be fairly driven. Whatever their
other flaws, laziness is usually not one of them. Suppose new
policies make it hard to make a fortune in finance. Does it seem
plausible that the people who currently go into finance to make
their fortunes will continue to do so, but be content to work for
ordinary salaries? The reason they go into finance is not because
they love finance but because they want to get rich. If the only
way left to get rich is to start startups, they'll start startups.
They'll do well at it too, because determination is the main factor
in the success of a startup.
[3]
And while it would probably be
a good thing for the world if people who wanted to get rich switched
from playing zero-sum games to creating wealth, that would not only
not eliminate great variations in wealth, but might even
exacerbate them.
In a zero-sum game there is at least a limit to the upside. Plus
a lot of the new startups would create new technology that further
accelerated variation in productivity.Variation in productivity is far from the only source of economic
inequality, but it is the irreducible core of it, in the sense that
you'll have that left when you eliminate all other sources. And if
you do, that core will be big, because it will have expanded to
include the efforts of all the refugees. Plus it will have a large
Baumol penumbra around it: anyone who could get rich by creating
wealth on their own account will have to be paid enough to prevent
them from doing it.You can't prevent great variations in wealth without preventing people
from getting rich, and you can't do that without preventing them
from starting startups.So let's be clear about that. Eliminating great variations in wealth would
mean eliminating startups. And that doesn't seem a wise move.
Especially since it would only mean you eliminated
startups in your own country. Ambitious people already move halfway
around the world to further their careers, and startups can operate
from anywhere nowadays. So if you made it impossible to get rich
by creating wealth in your country, people who wanted to do that
would just leave and do it somewhere else. Which would
certainly get you a lower Gini coefficient, along with a lesson in
being careful what you ask for.
[4]I think rising economic inequality is the inevitable fate of countries
that don't choose something worse. We had a 40 year stretch in the
middle of the 20th century that convinced some people otherwise.
But as I explained in The Refragmentation,
that was an anomaly — a
unique combination of circumstances that compressed American society
not just economically but culturally too.
[5]And while some of the growth in economic inequality we've seen since
then has been due to bad behavior of various kinds, there has
simultaneously been a huge increase in individuals' ability to
create wealth. Startups are almost entirely a product of this
period. And even within the startup world, there has been a qualitative
change in the last 10 years. Technology has decreased the cost of
starting a startup so much that founders now have the upper hand
over investors. Founders get less diluted, and it is now common
for them to retain
board control as well. Both further increase
economic inequality, the former because founders own more stock,
and the latter because, as investors have learned, founders tend
to be better at running their companies than investors.While the surface manifestations change, the underlying forces are
very, very old. The acceleration of productivity we see in Silicon
Valley has been happening for thousands of years. If you look at
the history of stone tools, technology was already accelerating in
the Mesolithic. The acceleration would have been too slow to
perceive in one lifetime. Such is the nature of the leftmost part
of an exponential curve. But it was the same curve.You do not want to design your society in a way that's incompatible
with this curve. The evolution of technology is one of the most
powerful forces in history.Louis Brandeis said "We may have democracy, or we may have wealth
concentrated in the hands of a few, but we can't have both." That
sounds plausible. But if I have to choose between ignoring him and
ignoring an exponential curve that has been operating for thousands
of years, I'll bet on the curve. Ignoring any trend that has been
operating for thousands of years is dangerous. But exponential
growth, especially, tends to bite you.___If accelerating variation in productivity is always going to produce
some baseline growth in economic inequality, it would be a good
idea to spend some time thinking about that future. Can you have
a healthy society with great variation in wealth? What would it
look like?Notice how novel it feels to think about that. The public conversation
so far has been exclusively about the need to decrease economic
inequality. We've barely given a thought to how to live with it.I'm hopeful we'll be able to. Brandeis was a product of the Gilded
Age, and things have changed since then. It's harder to hide
wrongdoing now. And to get rich now you don't have to buy politicians
the way railroad or oil magnates did.
[6]
The great concentrations
of wealth I see around me in Silicon Valley don't seem to be
destroying democracy.There are lots of things wrong with the US that have economic
inequality as a symptom. We should fix those things. In the process
we may decrease economic inequality. But we can't start from the
symptom and hope to fix the underlying causes.
[7]The most obvious is poverty. I'm sure most of those who want to
decrease economic inequality want to do it mainly to help the poor,
not to hurt the rich.
[8]
Indeed, a good number are merely being
sloppy by speaking of decreasing economic inequality when what they
mean is decreasing poverty. But this is a situation where it would
be good to be precise about what we want. Poverty and economic
inequality are not identical. When the city is turning off your
water
because you can't pay the bill, it doesn't make any difference
what <NAME>'s net worth is compared to yours. He might only
be a few times richer than you, and it would still be just as much
of a problem that your water was getting turned off.Closely related to poverty is lack of social mobility. I've seen
this myself: you don't have to grow up rich or even upper middle
class to get rich as a startup founder, but few successful founders
grew up desperately poor. But again, the problem here is not simply
economic inequality. There is an enormous difference in wealth
between the household <NAME> grew up in and that of a successful
startup founder, but that didn't prevent him from joining their
ranks. It's not economic inequality per se that's blocking social
mobility, but some specific combination of things that go wrong
when kids grow up sufficiently poor.One of the most important principles in Silicon Valley is that "you
make what you measure." It means that if you pick some number to
focus on, it will tend to improve, but that you have to choose the
right number, because only the one you choose will improve; another
that seems conceptually adjacent might not. For example, if you're
a university president and you decide to focus on graduation rates,
then you'll improve graduation rates. But only graduation rates,
not how much students learn. Students could learn less, if to
improve graduation rates you made classes easier.Economic inequality is sufficiently far from identical with the
various problems that have it as a symptom that we'll probably only
hit whichever of the two we aim at. If we aim at economic inequality,
we won't fix these problems. So I say let's aim at the problems.For example, let's attack poverty, and if necessary damage wealth
in the process. That's much more likely to work than attacking
wealth in the hope that you will thereby fix poverty.
[9]
And if
there are people getting rich by tricking consumers or lobbying the
government for anti-competitive regulations or tax loopholes, then
let's stop them. Not because it's causing economic inequality, but
because it's stealing.
[10]If all you have is statistics, it seems like that's what you need
to fix. But behind a broad statistical measure like economic
inequality there are some things that are good and some that are
bad, some that are historical trends with immense momentum and
others that are random accidents. If we want to fix the world
behind the statistics, we have to understand it, and focus our
efforts where they'll do the most good.Notes[1]
<NAME>. The Price of Inequality. Norton, 2012. p.
32.[2]
Particularly since economic inequality is a matter of outliers,
and outliers are disproportionately likely to have gotten where
they are by ways that have little do with the sort of things
economists usually think about, like wages and productivity, but
rather by, say, ending up on the wrong side of the "War on Drugs."[3]
Determination is the most important factor in deciding between
success and failure, which in startups tend to be sharply differentiated.
But it takes more than determination to create one of the hugely
successful startups. Though most founders start out excited about
the idea of getting rich, purely mercenary founders will usually
take one of the big acquisition offers most successful startups get
on the way up. The founders who go on to the next stage tend to
be driven by a sense of mission. They have the same attachment to
their companies that an artist or writer has to their work. But
it is very hard to predict at the outset which founders will do
that. It's not simply a function of their initial attitude. Starting
a company changes people.[4]
After reading a draft of this essay, <NAME> told me
how he had once talked to a group of Europeans "who said
they wanted to make Europe more entrepreneurial and more
like Silicon Valley. I said by definition this will give you more
inequality. They thought I was insane — they could not process
it."[5]
Economic inequality has been decreasing globally. But this
is mainly due to the erosion of the kleptocracies that formerly
dominated all the poorer countries. Once the playing field is
leveler politically, we'll see economic inequality start to rise
again. The US is the bellwether. The situation we face here, the
rest of the world will sooner or later.[6]
Some people still get rich by buying politicians. My point is that
it's no longer a precondition.[7]
As well as problems that have economic inequality as a symptom,
there are those that have it as a cause. But in most if not all,
economic inequality is not the primary cause. There is usually
some injustice that is allowing economic inequality to turn into
other forms of inequality, and that injustice is what we need to
fix. For example, the police in the US treat the poor worse than
the rich. But the solution is not to make people richer. It's to
make the police treat people more equitably. Otherwise they'll
continue to maltreat people who are weak in other ways.[8]
Some who read this essay will say that I'm clueless or even
being deliberately misleading by focusing so much on the richer end
of economic inequality — that economic inequality is really about
poverty. But that is exactly the point I'm making, though sloppier
language than I'd use to make it. The real problem is poverty, not
economic inequality. And if you conflate them you're aiming at the
wrong target.Others will say I'm clueless or being misleading by focusing on
people who get rich by creating wealth — that startups aren't the
problem, but corrupt practices in finance, healthcare, and so on.
Once again, that is exactly my point. The problem is not economic
inequality, but those specific abuses.It's a strange task to write an essay about why something isn't the
problem, but that's the situation you find yourself in when so many
people mistakenly think it is.[9]
Particularly since many causes of poverty are only partially
driven by people trying to make money from them. For example,
America's abnormally high incarceration rate is a major cause of
poverty. But although for-profit prison companies and
prison guard unions both spend
a lot lobbying for harsh sentencing laws, they
are not the original source of them.[10]
Incidentally, tax loopholes are definitely not a product
of some power shift due to recent increases in economic inequality.
The golden age of economic equality in the mid 20th century was
also the golden age of tax avoidance. Indeed, it was so widespread
and so effective that I'm skeptical whether economic inequality was
really so low then as we think. In a period when people are trying
to hide wealth from the government, it will tend to be hidden from
statistics too. One sign of the potential magnitude of the problem
is the discrepancy between government receipts as a percentage of
GDP, which have remained more or less constant during the entire
period from the end of World War II to the present, and tax rates,
which have varied dramatically.
Thanks to <NAME>, <NAME>, <NAME>, <NAME>, <NAME>, <NAME>, <NAME>, <NAME>, <NAME>, <NAME>, and <NAME> for reading
drafts of this.Note: This is a new version from which I
removed a pair of metaphors that made a lot of people mad,
essentially by macroexpanding them. If anyone wants to see
the old version, I put it here.Related:The Short VersionA Reply to Ezra KleinA Reply to Russell OkungFrench Translation
|
|
https://github.com/Jarmos-san/resume | https://raw.githubusercontent.com/Jarmos-san/resume/main/README.md | markdown | Creative Commons Attribution Share Alike 4.0 International | # Resume
The contents of this repository is how I create my resume using
[Typst](https://typst.app). Its a modern alternative to LaTeX with an intuitive
and easy-to-use syntax.
Do note, the project is still work-in-progress and hence will take a while to
complete. But if you want to check out a template resume, check out this
[Google Doc template](https://docs.google.com/document/d/12jBHnaiQXpIVH91lHf3OvNA5hPdFpmi5PBK5wUE5C_0/edit?usp=drive_link)
for now.
|
https://github.com/dainbow/MatGos | https://raw.githubusercontent.com/dainbow/MatGos/master/themes/23.typ | typst | #import "../conf.typ": *
= Общее решение системы линейных алгебраических уравнений. <NAME>-Капелли.
== Общее решение системы линейных алгебраических уравнений
#definition[
*Группой* называется множество $G$ с определённой на нём бинарной операцией
умножения $dot: G times G -> G$, удовлетворяющей следующим условиям:
- (Ассоциативность)
#eq[
$forall a, b, c in G : space (a b) c = a (b c)$
]
- (Существование нейтрального элемента)
#eq[
$exists e in G : forall a in G : space a e = e a = a$
]
- (Существование нейтрального элемента)
#eq[
$forall a in G : exists a^(-1) in G : space a a^(-1) = a^(-1)a = e$
]
]
#definition[
Группа $(G, dot)$ называется *абелевой*, если умножение в ней коммутативно, то
есть
#eq[
$forall a, b in G : space a b = b a$
]
]
#definition[
*Кольцом* называется множество $R$ с определёнными на нём бинарными операциями
сложения $+: R times R -> R$ и умножения $dot: R times R -> R$, удовлетворяющая
следующим условиям:
- $(R, +)$ -- абелева группа, нейтральный элемент в которой обозначается через $0$.
- (Ассоциативность умножения)
#eq[
$forall a, b, c in R : space (a b) c = a(b c)$
]
- (Дистрибутивность умножения относительно сложения)
#eq[
$forall a, b, c in R : space a(b + c) = a b + a c and (a + b)c = a c + b c$
]
- (Существование нейтрального элемента относительно умножения)
#eq[
$exists 1 in R : forall a in R : space a 1 = 1 a = a$
]
]
#definition[
Кольцо $(R, +)$ называется *коммутативным*, если умножение в нём коммутативно,
то есть
#eq[
$forall a, b in R : space a b = b a$
]
]
#definition[
Пусть $(R, +, dot)$ -- кольцо.
Элемент $a in R$ называется *обратимым*, если
#eq[
$exists a^(-1) in R : space a a^(-1) = a^(-1)a = 1$
]
*Группой обратимых элементов* кольца $(R, +, dot)$ называется множество $R^*$ его
обратимых элементов.
]
#definition[
*Полем* называется такое коммутативное кольцо $(FF, +, dot)$, для которого
выполнено равенство $FF^* = FF without {0}$.
]
#definition[
*Линейным пространством*, или *векторным пространством* над полем $FF$ называется
абелева группа $(V, +)$, на которой определено умножение на элементы поля $dot: FF times V -> V$,
удовлетворяющее следующим условиям:
- $forall alpha, beta in FF : forall v in V : space (alpha + beta)v = alpha v + beta v$
- $forall alpha in FF : forall u,v in V : space alpha(u + v) = alpha u + alpha v$
- $forall alpha, beta in FF : forall v in V : space (alpha beta)v = alpha(beta v)$
- $forall v in V : space 1 v = v$
Элементы поля $FF$ называются *скалярами*, элементы группы $V$ -- *векторами*.
]
#definition[
Пусть $A = (a_(i j)) in M_(k times n)(FF); b = (b_i) in FF^n$.
*Системой линейных уравнений* $A x = b$ называется следующая система:
#eq[
$cases(
a_(1 1) x_1 + a_(1 2) x_2 + ... + a_(1 n) x_n = b_1,
a_(2 1) x_1 + a_(2 2) x_2 + ... + a_(2 n) x_n = b_2,
..., a_(k 1) x_1 + a_(k 2) x_2 + ... + a_(k n) x_n = b_k,
)$
]
Матрица $A$ называется *матрицей системы*, матрица $(A | b)$ -- *расширенной матрицей системы*
]
#definition[
Система линейных уравнений $A x = b$ называется:
- *Однородной*, если $b = 0$
- *Совместной*, если множество её решений непусто
]
#definition[
*Фундаментальной системой решений* однородной системы $A x = 0$ называется базис
пространства её решений.
Матрица, образованная столбцами фундаментальной системы решений, называется
*фундаментальной матрицей системы* и обозначается через $Phi$.
]
#proposition[
Множество решений однородной системы $A x = 0$ является линейным пространством.
]
#proof[
Все требования линейного пространства очевидны.
]
#proposition[
Пусть $A x = b$ -- совместная система, $x_0 in FF^n$ -- решение системы, $V$ -- пространство
решений однородной системы $A x = 0$.
Тогда множество решений системы $A x = b$ имеет вид
#eq[
$x_0 + V = {x_0 + v | v in V}$
]
]
#proof[
Пусть $U$ -- множество решений системы $A x = b$.
- Если $v in V$, то $A(x_0 + v) = A x_0 + A v = b => x_0 + v in U$.
- Если $u in U$, то $A(u - x_0) = 0 => u - x_0 in V$
Таким образом, $U = x_0 + V$
]
== Теорема Кронекера-Капелли
#definition[
Системы $A x = b$ и $A' x = b'$ называются *эквивалентными*, если множества их
решений совпадают.
]
#definition[
*Элементарными преобразованиями* строк матрицы $A in M_(n times k)(FF)$ называются
следующие операции:
- Прибавление к $i$-й строке $j$-й строки, умноженной на скаляр $alpha in FF; quad i, j in overline("1,n"); i != j$
- Умножение $i$-й строки на скаляр $lambda in FF^*; i = overline("1, n")$
- Перестановка $i$-й и $j$-й строк местами; $i, j in overline("1, n"); i != j$
]
#definition[
*Элементарными матрицами* порядка $n in NN$ называются матрицы, умножение слева
на которые приводит к осуществлению соответствующего элементарного
преобразования строк над матрицей с $n$ строками:
- $D_(i j)(alpha) := E + alpha E_(i, j); quad i,j in overline("1,n"); i != j$
- $T_i(lambda) := E + (lambda - 1)E_(i i); quad i in overline("1,n")$
- $P_(i j) := E - (E_(i i) + E_(j j)) + (E_(i j) + E_(j i))$
]
#definition[
Матрица $A in M_n (FF)$ называется *обратимой*, если существует матрица $A^(-1) in M_n (FF)$ такая,
что $A A^(-1) = A^(-1) A = E$.
]
#proposition[
Элементарные матрицы любого порядка $n$ обратимы
]
#proof[
Предъявим обратные матрицы в явном виде:
- $(D_(i j)(alpha))^(-1) = D_(j i) (-alpha)$
- $(T_i (lambda))^(-1) = T_i (lambda^(-1))$
- $(P_(i j))^(-1) = P_(i j)$
]
#proposition[
Элементарные преобразования строк расширенной матрицы переводят её в
эквивалентную.
]
#definition[
*Главным элементом* строки называется её первый ненулевой элемент.
]
#definition[
Матрица $A in M_(n times k)(FF)$ имеет *ступенчатый вид*, если номера главных
элементов её строк строго возрастают.
При этом если в матрице есть нулевые строки, то они расположены внизу матрицы.
]
#theorem(
"Метод Гаусса",
)[
Любую матрицу $A in M_(n times k)(FF)$ элементарными преобразованиями можно
привести к ступенчатому виду
]
#proof[
Предъявим алгоритм:
+ Если $A = 0$, то она уже имеет ступенчатый вид, завершаем процедуру.
+ Пусть $j in overline("1, k")$ -- наименьший номер ненулевого столбца. Переставим
строки так, чтобы $a_(1 j)$ стал ненулевым.
+ Для всех $i in overline("2, n")$ к $i$-й строке прибавим первую, умноженную на $-a_(i j)(a_(1 j))^(-1)$.
Тогда все элементы $a_(2 j), ..., a_(n j)$ станут нулевыми
+ Пусть матрица была приведена к виду $A'$. Если она ступенчатая, то
останавливаемся. Если она не ступенчатая, то начинаем заново для подматрицы $B$ расположенной
на пересечении строк с номерами $overline("2,n")$ и столбцом с номерами $(overline("j+1,k"))$.
Дальнейшие преобразования не изменят элементов за пределами этой подматрицы.
]
#definition[
Пусть $V$ -- конечномерное линейное пространство, $X subset V$.
*Рангом* системы $X$ называется наибольший размер линейно независимой подсистемы
в $X$.
Обозначение -- $"rk" X$.
]
#definition[
Пусть $A in M_(n times k)(FF)$
- *Строчным рангом* матрицы $A$ называется ранг $"rk"_r A$ системы её строк.
- *Столбцовым рангом* матрицы $A$ называется ранг $"rk"_c A$ системы её столбцов.
]
#theorem[
Для любой матрицы $A in M_(n times k)(FF)$ выполнено следующее равенство:
#eq[
$"rk"_r A = "rk"_c A$
]
]
#definition[
*Рангом матрицы* $A in M_(n times k)(FF)$ называется её строчный или столбцовый
ранг.
Обозначение -- $"rk" A$.
]
#proposition[
Пусть $A in M_(n times k)(FF); B in M_(k times M) (FF)$, причём столбцы матрицы $A$ линейно
независимы. Тогда
#eq[
$"rk" A B = "rk" B$
]
]
#note[
В том числе, элементарные преобразования не меняют ранг матрицы.
]
#proposition[
Ранг ступенчатой матрицы $A in M_(n times k)(FF)$ равен числу ступеней.
]
#theorem("Кронекера-Капелли")[
#eq[
$"Система" A x = b "совместна" <=> "rk" A = "rk" (A | b)$
]
]
#proof[
Приведём расширенную матрицу системы $(A | b)$ к упрощённому виду $(A' | b')$.
Тогда система совместна $<=>$ в $(A' | b')$ нет ступеньки, начинающейся в
столбце $b' <=>$ у $A'$ и $(A' | b')$ одно и то же число ступенек $<=>$ $"rk" A = "rk" (A | b)$.
]
|
|
https://github.com/augustebaum/tenrose | https://raw.githubusercontent.com/augustebaum/tenrose/main/examples/relative.typ | typst | MIT License | #import "@preview/diagraph:0.2.2": *
= 100%
#raw-render(```
digraph {
rankdir=LR
"Hello" -> "World"
"World" -> "!"
}
```, width: 100%)
= 50%
#raw-render(```
digraph {
rankdir=LR
"Hello" -> "World"
"World" -> "!"
}
```, width: 50%)
= 5%
#raw-render(```
digraph {
rankdir=LR
"Hello" -> "World"
"World" -> "!"
}
```, width: 5%) |
https://github.com/xdoardo/co-thesis | https://raw.githubusercontent.com/xdoardo/co-thesis/master/thesis/chapters/imp/semantics.typ | typst | #import "@preview/prooftrees:0.1.0"
#import "/includes.typ": *
== Semantics <imp-semantics>
Having understood the syntax of Imp, we can move to the _meaning_ of Imp
programs. We will explore the operational semantics of the language using the
formalism of inference rules, then we will show the implementation of the
semantics (as an intepreter) for these rules.
Before describing the rules of the semantics, we will give a brief explaination
of what we expect to be the result of the evaluation of an Imp program.
#code(label: <code-imp-simple>)[`if true then skip else skip`]
An example of Imp program is shown in @code-imp-simple. In general, we can
expect the evaluation of an Imp program to terminate in some kind value or
diverge. But what happens when, as mentioned in
@subsection-imp-introduction-syntax[Subsection], an unitialized identifier is
used, as shown for example in @code-imp-failing? The execution of the program
cannot possibly continue, and we define such a state as _failing_ or _stuck_
(see also @section-convergence[Section]).
Of course, there is a plethora of other kinds of failures we could model, both
deriving from static analysis or from the dynamic execution of the program (for
example, in a language with divisions, a division by 0), but we chose to model
this kind of behaviour only.
#code(label: <code-imp-failing>)[`while true do x <- y`]
We can now introduce the formal notation we will use to describe the semantics
of Imp programs. We already introduced the concept of store, which keeps track
of the mutation of identifiers and their value during the execution of the
program. We write #conv([c, $sigma$], $sigma_1$) to mean that the program $c$,
when evaluated starting from the context $sigma$, converges to the store
$sigma_1$; we write #fails([c, $sigma$]) to say that the program $c$, when
evaluated in context $sigma$, does not converge to a result but, instead,
execution gets stuck (that is, an unknown identifier is used).
The last possibility is for the execution to diverge, #div([c, $sigma$]): this
means that the evaluation of the program never stops and while no state of
failure is reached no result is ever produced. An example of this behaviour is
seen when evaluating @code-imp-diverging.
#code(label: <code-imp-diverging>)[`while true do skip`]
We are now able to give inference rules for each construct of the Imp language:
we will start from simple ones, that is arithmetic and boolean expressions, and
we will then move to commands. The inference rules we give follow the formalism
of *big-step* operational semantics, that is, intermediate states of evaluation
are not shown explicitly in the rules themselves.
=== Arithmetic expressions <imp-semantics-arithmetic_expressions>
Arithmetic expressions in Imp can be of three kinds: integer ($ZZ$) constants,
identifiers and sums. As anticipated, the evaluation of arithmetic expressions
can fail, that is, the evaluation of arithmetic expressions is not a total
function; again, the possibile erroneous states we can get into when evaluating
an arithmetic expression mainly concerns the use of undeclared identifiers.
Without introducing them, we will use notations similar to that used earlier for
commands, in particular #conv($dot.c$, $dot.c$).
#figure(
grid(
columns: (1fr, 1fr, 1fr),
rows: (40pt),
prooftrees.tree(prooftrees.axi[], prooftrees.uni[#conv([const n, $sigma$], [n])]),
prooftrees.tree(
prooftrees.axi[$id in sigma$],
prooftrees.uni[#conv([var id, $sigma$], [$sigma id$])],
),
prooftrees.tree(
prooftrees.axi(pad(bottom: 4pt, [#conv([$a_1$ , $sigma$], [$n_1$])])),
prooftrees.axi(pad(bottom: 4pt, [#conv([$a_2$, $sigma$], [$n_2$])])),
prooftrees.nary(2)[#conv([$"plus" a_1 a_2$, $sigma$], [$(n_1 + n_2)$])],
),
),
caption: "Inference rules for the semantics of arithmetic expressions of Imp",
supplement: "Table",
)<imp-arith-semantics>
The Agda code implementing the interpreter for arithmetic expressions is shown
in @code-aeval. As anticipated, the inference rules denote a partial
function; however, since the predicate $id in sigma$ is decidable, we can make
the interpreter target the `Maybe` monad and make the intepreter a total
function.
#mycode(label: <code-aeval>, "https://github.com/ecmma/co-thesis/blob/master/agda/lujon/Imp/Semantics/BigStep/Functional/Arith.agda#L16")[
//typstfmt::off
```hs
aeval : ∀ (a : AExp) (s : Store) -> Maybe ℤ
aeval (const x) s = just x
aeval (var x) s = s x
aeval (plus a a₁) s = aeval a s >>= λ v₁ -> aeval a₁ s >>= λ v₂ -> just (v₁ + v₂)
```
//typstfmt::on
]
=== Boolean expressions <imp-semantics-boolean_expressions>
Boolean expressions in Imp can be of four kinds: boolean constants, negation of
a boolean expression, logical conjunction and, finally, comparison of arithmetic
expressions.
#figure(
grid(
columns: (1fr, 1fr),
rows: (40pt, 40pt),
prooftrees.tree(prooftrees.axi[], prooftrees.uni[#conv([const c, $sigma$], [c])]),
prooftrees.tree(
prooftrees.axi(pad(bottom: 2pt, [#conv([b, $sigma$], [c])])),
prooftrees.uni[#conv([$not b$, $sigma$], [$not c$])],
),
prooftrees.tree(
prooftrees.axi(pad(bottom: 4pt, [#conv([$a_1$, $sigma$], [$n_1$])])),
prooftrees.axi(pad(bottom: 4pt, [#conv([$a_2$, $sigma$], [$n_2$])])),
prooftrees.nary(2)[#conv([le $a_1$ $a_2$, $sigma$], [$(n_1 < n_2)$])],
),
prooftrees.tree(
prooftrees.axi(pad(bottom: 4pt, [#conv([$b_1$, $sigma$], [$c_1$])])),
prooftrees.axi(pad(bottom: 4pt, [#conv([$b_2$, $sigma$], [$c_2$])])),
prooftrees.nary(2)[#conv([and $b_1$ $b_2$, $sigma$], [$(c_1 and c_2)$])],
)
),
caption: "Inference rules for the semantics of boolean expressions of Imp",
supplement: "Table",
)<imp-bool-semantics>
The line of reasoning for the concrete implementation in Agda is the same as
that for arithmetic expressions: the inference rules denote a partial function;
since what makes this function partial -- the definition of identifiers -- is a
decidable property, we can make the interpreter for boolean expressions a total function
using the `Maybe` monad, as shown in @code-beval.
#mycode(label: <code-beval>,"https://github.com/ecmma/co-thesis/blob/master/agda/lujon/Imp/Semantics/BigStep/Functional/Bool.agda#L20")[
//typstfmt::off
```hs
beval : ∀ (b : BExp) (s : Store) -> Maybe Bool
beval (const c) s = just c
beval (le a₁ a₂) s = aeval a₁ s >>=
λ v₁ -> aeval a₂ s >>=
λ v₂ -> just (v₁ ≤ᵇ v₂)
beval (not b) s = beval b s >>= λ b -> just (bnot b)
beval (and b₁ b₂) s = beval b₁ s >>=
λ b₁ -> beval b₂ s >>=
λ b₂ -> just (b₁ ∧ b₂)
```
//typstfmt::on
]
=== Commands <imp-semantics-commands>
#figure(
tablex(
columns: (140pt, auto, 160pt, 60pt),
auto-vlines: false,
auto-hlines: false,
prooftrees.tree(prooftrees.axi[], prooftrees.uni[#conv([skip , $sigma$], [$sigma$])]),
[$arrow.b.double$skip],
prooftrees.tree(
prooftrees.axi(pad(bottom: 2pt, [#conv([a , $sigma$], [v])])),
prooftrees.uni[#conv([$"assign" id a$, $sigma$], [$"update" id v space sigma$])],
),
[$arrow.b.double$assign],
prooftrees.tree(
prooftrees.axi(pad(bottom: 5pt, [#conv([$c_1$, $sigma$], [$sigma_1$])])),
prooftrees.axi(pad(bottom: 5pt, [#conv([$c_2$, $sigma_1$], [$sigma_2$])])),
prooftrees.nary(2)[#conv([$"seq" space c_1 space c_2$, $sigma$], [$sigma_2$])],
),
[$arrow.b.double$seq],
prooftrees.tree(
prooftrees.axi(pad(bottom: 5pt, [#conv([$c^t$, $sigma$], [$sigma^t$])])),
prooftrees.axi(pad(bottom: 5pt, [#conv([$b$, $sigma$], [$"true"$])])),
prooftrees.nary(2)[#pad(top: 5pt, conv([$"if" b "then" c^t "else" c^f$, $sigma$], [$sigma^t$]))],
),
[$arrow.b.double$if-true],
prooftrees.tree(
prooftrees.axi(pad(bottom: 5pt, [#conv([$c^f$, $sigma$], [$sigma^f$])])),
prooftrees.axi(pad(bottom: 5pt, [#conv([$b$, $sigma$], [$"false"$])])),
prooftrees.nary(2)[#pad(top: 5pt, conv([$"if" b "then" c^t "else" c^f$, $sigma$], [$sigma^f$]))],
),
[$arrow.b.double$if-false],
prooftrees.tree(
prooftrees.axi(pad(bottom: 5pt, [#conv([$b$, $sigma$], [$"false"$])])),
prooftrees.uni[#pad(top: 5pt, conv([$"while" b "do" c$, $sigma$], [$sigma$]))],
),
[$arrow.b.double$while-false],
colspanx(4, align: center,
grid(columns: 2,
column-gutter: 10pt,
prooftrees.tree(
prooftrees.axi(pad(bottom: 5pt, [#conv([$b$, $sigma$], [$"true"$])])),
prooftrees.axi(pad(bottom: 5pt, [#conv([$c$, $sigma$], [$sigma'$])])),
prooftrees.cobin[#conv([$"while" b "do" c$, $sigma$], [$sigma'$])],
), [#v(50%)$arrow.b.double$while-true#v(50%)])),
),
caption: "Inference rules for the semantics of commands",
supplement: "Table",
)<imp-commands-semantics>
We need to be careful when examining the inference rules in
@imp-commands-semantics. Although they are graphically rendered the same, the
convergency propositions used in the inference rules are different from those
in @imp-semantics-boolean_expressions or @imp-semantics-arithmetic_expressions.
In fact, while in the latter the only modeled effect is a decidable one, the
convergency proposition here models two effects, partiality and failure. While
failure, intended as we did before, is a decidable property, partiality is not,
and we cannot design an interpreter for these rules targeting the `Maybe` monad
only: we must thus combine the effects and target the `FailingDelay` monad, as
shown in @section-convergence[Section]. The code for the intepreter is shown in
@code-ceval.
#mycode(label: <code-ceval>, "https://github.com/ecmma/co-thesis/blob/master/agda/lujon/Imp/Semantics/BigStep/Functional/Command.agda#L23")[
//typstfmt::off
```hs
mutual
ceval-while : ∀ {i} (c : Command) (b : BExp) (s : Store)
-> Thunk (Delay (Maybe Store)) i
ceval-while c b s = λ where .force -> (ceval (while b c) s)
ceval : ∀ {i} -> (c : Command) -> (s : Store) -> Delay (Maybe Store) i
ceval skip s = now (just s)
ceval (assign id a) s =
now (aeval a s) >>= λ v -> now (just (update id v s))
ceval (seq c c₁) s =
ceval c s >>= λ s' -> ceval c₁ s'
ceval (ifelse b c c₁) s =
now (beval b s) >>= (λ bᵥ -> (if bᵥ then ceval c s else ceval c₁ s))
ceval (while b c) s =
now (beval b s) >>=
(λ bᵥ -> if bᵥ
then (ceval c s >>= λ s -> later (ceval-while c b s))
else now (just s))
```
//typstfmt::on
]
The last rule (`while` for `beval b` converging to `just true`) is coinductive,
and this is reflected in the code by having the computation happen inside a
`Thunk` (see @subsubsection-sizes-coinduction[Section])
=== Properties of the interpreter
Regarding the intepreter, the most important property we want to show puts in
relation the starting store a command is evaluated in and the (hypothetical)
resulting store. Up until now, we kept the mathematical layer and the code layer
separated; from now on we will collapse the two and allow ourselves to use
mathematical notation to express formal statements about the code: in practice,
this means that, for example, the mathematical names $"aeval"$,
$"beval"$ and $"ceval"$ refer to names from the "code layer"
//typstfmt::off
```hs aeval```, ```hs beval``` and ```hs ceval```, respectively.
//typstfmt::on
#lemma(label: <lemma-ceval-store-tilde>)[
Let $c$ be a command and $sigma_1$ and $sigma_2$ be two stores. Then
#align(
center,
$#conv($"ceval" c , sigma_1$, $sigma_2$) -> sigma_1 space ∻ sigma_2$,
)
#mycode(proof: <proof-ceval-store-tilde>, "https://github.com/ecmma/co-thesis/blob/master/agda/lujon/Imp/Semantics/BigStep/Functional/Properties.agda#L90")[
//typstfmt::off
```hs
ceval⇓=>∻ : ∀ (c : Command) (s s' : Store) (h⇓ : (ceval c s) ⇓ s') -> s ∻ s'
```
//typstfmt::on
]]
@lemma-ceval-store-tilde[Lemma] will be fundamental for later proofs.
It is also important, now that all is set up, to underline that the meaning of
#conv([c, $sigma$], $sigma_1$), #fails([c, $sigma$]) and #div([c, $sigma$])
which we used giving an intuitive description but without a concrete
definition, are exactly the types described in @section-convergence[Section],
with the parametric types adapted to the situation at hand: thus, saying
#conv([c, $sigma$], $sigma_1$) actually means that $"ceval" space "c" space
sigma ≋ "now" ("just" sigma_1)$, #div([c, $sigma$]) means that $"ceval" space
"c" space sigma ≋ "never"$ and #fails([c, $sigma$]) means that $"ceval"
space "c" space sigma ≋ "now" "nothing"$.
|
|
https://github.com/valentinvogt/npde-summary | https://raw.githubusercontent.com/valentinvogt/npde-summary/main/README.md | markdown | # NumPDE 2024 Summary
Tutorial class 2024 for *Numerical Methods for Partial Differential Equation* at ETH Zürich.
On this repository you can find the [typst](https://typst.app/) source files for the TA summary.
This summary is based on the [NumPDE 2023 summary](https://www.overleaf.com/5644262547pnpdgpmjjmcj) written in LaTeX.
Credit to the 2023 TAs for creating the summary.
## PDFs
You can find compiled PDFs under [releases](https://github.com/valentinvogt/npde-summary/releases).
## Contributions
If you find any errors in the summary or want to make some other contribution
to the notes, then you are very welcome to open an issue or create a pull request.
|
|
https://github.com/tani-mss/onjuku2024 | https://raw.githubusercontent.com/tani-mss/onjuku2024/main/slide.typ | typst | #import "@preview/touying:0.5.2": *
#import themes.stargazer: *
#import "@preview/tiaoma:0.2.0": *
#import "@preview/colorful-boxes:1.3.1": *
#import "@preview/prooftrees:0.1.0": *
#import "@preview/numbly:0.1.0": numbly
#show: stargazer-theme.with(
aspect-ratio: "16-9",
config-info(
title: [ランベック計算と文脈自由文法・線形文法・正規文法],
author: [谷口雅弥],
date: datetime.today(),
institution: [理化学研究所]
),
)
// For Japanese
// #set text(font: "Hiragino Kaku Gothic ProN", lang: "ja")
#set text(font: "Harano Aji Gothic", lang: "ja")
// #set text(font: "Harano Aji Mincho", lang: "ja")
// #show regex("[\p{scx:Han}\p{scx:Hira}\p{scx:Kana}]"): set text(font: "Noto Serif CJK JP", lang: "ja")
#set heading(numbering: numbly("{1}.", default: "1.1"))
#let myaxi(body) = axi(pad(bottom: 6pt, top: 6pt, body))
#let myuni(body) = uni(pad(bottom: 6pt, top: 6pt, body))
#let mybin(body) = bin(pad(bottom: 6pt, top: 6pt, body))
#let half(body) = block(width: 60%, body)
#title-slide()
#slide[
文が妥当であることは、論理式が証明できることであり\
論理式が証明できることは、文が妥当であることである。
]
#outline-slide()
= まえおき
== 自己紹介
- 谷口雅弥 (博士(情報科学, JAIST))
- 理化学研究所 革新知能統合研究センター 自然言語理解チーム
- 東北大学 自然言語処理研究グループ
- 形式言語理論(範疇文法)・数理論理学(部分構造論理)
== 配布スライド
#slide[
#set align(center)
`https://tani-mss.github.io/onjuku2024/slide.pdf`
#qrcode(
"https://tani-mss.github.io/onjuku2024/slide.pdf",
options: (scale: 4.0)
)
]
= 背景: ランベック計算と文脈自由文法
#focus-slide[
論理学のはなし
]
== ランベック計算の紹介
#outline-colorbox(title: [ランベック計算 (Lambek, 1958) $bold(L)^bullet$])[
#v(5pt)
小文字のアルファベットは原子論理式とする。
小文字のギリシャ文字は式 ($phi := a | phi slash phi | phi backslash phi$) であり大文字のギリシャ文字は式の列である。推論規則は以下。
#grid(
columns: (200pt,) * 3,
column-gutter: 50pt,
row-gutter: 10pt,
tree(
myaxi[],
myuni[$alpha => alpha$]
),
tree(
myaxi[$Sigma, alpha => beta$],
myuni[$Sigma => beta slash alpha$],
),
tree(
myaxi[$alpha,Sigma => beta$],
myuni[$Sigma => alpha backslash beta$],
),
tree(
myaxi[$Gamma,alpha,Delta => beta$],
myaxi[$Sigma => alpha$],
mybin[$Gamma,Sigma,Delta => beta$]
),
tree(
myaxi[$Gamma,alpha,Delta => beta$],
myaxi[$Sigma => gamma$],
mybin[$Gamma,alpha slash gamma, Sigma,Delta => beta$]
),
tree(
myaxi[$Gamma,alpha,Delta => beta$],
myaxi[$Sigma => gamma$],
mybin[$Gamma,Sigma,gamma backslash alpha,Delta => beta$]
),
tree(
myaxi[$Gamma,alpha,beta,Delta => beta$],
myuni[$Gamma,alpha bullet beta,Delta => beta$],
),
tree(
myaxi[$Gamma => alpha$],
myaxi[$Delta => beta$],
mybin[$Gamma,Delta => alpha bullet beta$],
),
)
]
== プロダクトフリーランベック計算
#outline-colorbox(title: [プロダクトフリーランベック計算 $bold(L)$])[
#v(5pt)
小文字のアルファベットは原子論理式とする。
小文字のギリシャ文字は式 ($phi := a | phi slash phi | phi backslash phi$) であり大文字のギリシャ文字は式の列である。推論規則は以下。
#grid(
columns: (200pt,) * 3,
column-gutter: 50pt,
row-gutter: 10pt,
tree(
myaxi[],
myuni[$a => a$]
),
tree(
myaxi[$Sigma, alpha => beta$],
myuni[$Sigma => beta slash alpha$],
),
tree(
myaxi[$alpha,Sigma => beta$],
myuni[$Sigma => alpha backslash beta$],
),
tree(
myaxi[$Gamma,alpha,Delta => beta$],
myaxi[$Sigma => alpha$],
mybin[$Gamma,Sigma,Delta => beta$]
),
tree(
myaxi[$Gamma,alpha,Delta => beta$],
myaxi[$Sigma => gamma$],
mybin[$Gamma,alpha slash gamma, Sigma,Delta => beta$]
),
tree(
myaxi[$Gamma,alpha,Delta => beta$],
myaxi[$Sigma => gamma$],
mybin[$Gamma,Sigma,gamma backslash alpha,Delta => beta$]
)
)
]
#outline-colorbox(title: [カット除去定理 (Lambek 1958)])[
#v(5pt)
$L$ は規則の集合とする。
$L in {bold(L),bold(L)^bullet};[L tack Gamma => alpha quad <==> quad L backslash {"cut"} tack Gamma => alpha]$
]
#focus-slide[
言語のはなし
]
== 文脈自由文法
#outline-colorbox(title: [文脈自由文法])[
#v(5pt)
大文字は非終端記号、小文字は終端記号とする。このとき、$A <- a$, $A <- B C$ で書かれる文法規則の集合を文脈自由文法とする。\ (一般には、もと緩く定義できるが、チョムスキー標準形を採用する)
]
#outline-colorbox(title: [文脈自由言語])[
#v(5pt)
文法にもとづいた書き換えによって生成される終端記号の列 (文)の集まりを言語と呼び、とくに文脈自由文法にもとづく言語を文脈自由言語とよぶ。
]
== 文脈自由文法との対応
ランベック計算の体系を$bold(L) = {"Ax", "Cut", "I" slash, "I" backslash, slash "I", backslash "I"}$と表記する。
#outline-colorbox(title: [Language $frak(L)(ell,L)$])[
#v(5pt)
$bb(C)$ は式。$ell$ は語彙$Sigma arrow.r cal(P)(bb(C))$であり$[dot]_i$は選択$cal(P)(bb(C)) arrow.r bb(C)$。言語 $frak(L)$ は以下の通り:
$
frak(L)(ell, L,s) = {w_1,w_2,dots,w_n | exists [dot]_1,[dot]_2,dots,[dot]_n; L tack [ell(w_1)]_1, [ell(w_2)]_2,dots,[ell(w_n)]_n arrow.r.double s}
$
*以降では煩雑さを軽減するために 選択関数の添字を無視する*
]
#outline-colorbox(title: [Pentus 1993, 1997])[
#v(5pt)
$frak(L)(ell, bold(L),s)$ は文脈自由言語; つまり $sans(L)$は文脈自由言語 iff. $exists ell[sans(L)=frak(L)(ell, bold(L), S)]$
]
#outline-colorbox(title: [言語のカット除去定理(谷口))])[
#v(5pt)
カット除去定理から次が直ちに導かれる。$frak(L)(ell, L, S) = frak(L)(ell, L backslash {"cut"}, S)$
]
== ランベック計算と文脈自由文法の関係
= ランベック計算と線形文法
#focus-slide[
論理のはなし
]
== ランベック文法の断片
#outline-colorbox(title: [ランベック計算の断片 $bold(L)(slash,backslash)$])[
#v(5pt)
小文字のアルファベットは原子論理式とする。
小文字のギリシャ文字は式 ($phi := a | phi slash phi | phi backslash phi$) であり大文字のギリシャ文字は式の列である。推論規則は以下。
#grid(
columns: (60pt,150pt,150pt,150pt),
column-gutter: 50pt,
row-gutter: 10pt,
tree(
myaxi[],
myuni[$a => a$]
),
tree(
myaxi[$Gamma,alpha,Delta => beta$],
myaxi[$Sigma => alpha$],
mybin[$Gamma,Sigma,Delta => beta$]
),
tree(
myaxi[$Gamma,alpha,Delta => beta$],
myaxi[$Sigma => gamma$],
mybin[$Gamma,alpha slash gamma, Sigma,Delta => beta$]
),
tree(
myaxi[$Gamma,alpha,Delta => beta$],
myaxi[$Sigma => gamma$],
mybin[$Gamma,Sigma,gamma backslash alpha,Delta => beta$]
)
)
]
#outline-colorbox(title: [カット除去定理(Zielonka 1976)])[
#v(5pt)
$L$ は規則の集合。
$L in {bold(L)(slash,backslash)};[L tack Gamma => alpha <==> L backslash {"cut"} tack Gamma => alpha]$
]
#outline-colorbox(title: [言語のカット除去定理(谷口))])[
#v(5pt)
カット除去定理から次が直ちに導かれる。$frak(L)(ell, L, S) = frak(L)(ell, L backslash {"cut"}, S)$
]
#focus-slide[
言語のはなし
]
== 線形文法
#outline-colorbox(title: "線形文法")[
#v(5pt)
$A <- a$, $A <- a B$, $A <- B a$の形で書かれる文法を線形文法と呼ぶ。\
もう少し緩い定義が一般的であるが、ここでは標準形として、これを採用する。\
一般には、規則の両辺に非終端記号が高々一つしか表われない文法規則である。
]
#outline-colorbox(title: [線形文法かつ正規文法でない例])[
#v(5pt)
以下より線形文法は正規文法だけでなく、文脈自由文法の一部も表現している。
$
A <- a B quad B <- A b quad B <- b quad quad sans(L) = {a^n b^n|n >= 1}
$
文脈自由文法以下の表現力であることは定義から直ちに導かれる。
]
#v(-15pt)
== 式の次数と語彙
#outline-colorbox(title: [線形文法とランベック計算の断片 (谷口)])[
#v(5pt)
式のうち演算子 $slash, backslash$ の数を式の次数と呼ぶ。\
語彙 $ell_1$ は 語彙のうち式の次数が高々1のものに限定したものとする。\
$sans(L)$ は線形言語とする。このとき $exists ell_1; sans(L) = frak(L)(ell_1, bold(L)(slash,backslash), S)$
]
*ランベック計算の断片と制約された語彙* は線形文法である!
== 線形文法とランベック計算の断片の関係の証明
#outline-colorbox(title: [主張])[
#v(5pt)
言語 $sans(L)_X$ は線形文法で生成される。ルートとなる非終端記号は$X$である。\
このとき、$s in L_X <==> s in frak(L)(ell_1,bold(L)(slash,backslash), X) $ となる語彙 $ell_1$が存在する。
]
#half[
*言語 $==>$ 論理*
*ベースケース*
長さが 1のとき$a in L_A$とする。
文法規則は $A <- a$ である。$ell_1$ は $ell_1(a) in.rev A$ とする。
このとき $s in frak(L)(ell_1, bold(L)(slash,backslash), A)$ が成り立つ。
*帰納ステップ*
長さが1より大きいとき、文法規則の形から
その文字列は $a overline(w)$ もしくは $overline(w) a$のどちらかに分割される。
]
#pagebreak()
#half[
*帰納ステップ 1* 長さが $n$ のとき、$a overline(w) in L_A$ とする。$overline(w)$ の長さが $n-1$ であるとする。
帰納法の仮定から $overline(w) in L_W ==> overline(w) in frak(L)(ell_1,bold(L)(slash,backslash), W)$。
文法規則は $A <- a W$ である。$ell_1$ は $ell_1(a) in.rev A slash W$ とする。
#tree(
myaxi[$[ell_1(overline(w))]=>W$],
myaxi[$A=>A$],
mybin[$A slash W, [ell_1(overline(w))] => A$],
myuni[$[ell_1(a)], [ell_1(overline(w))] => A$],
myuni[$[ell_1(a overline( w))] => A$]
)
したがって $a overline(w) in frak(L)(ell_1, bold(L)(slash, backslash), A)$ である。
]
#pagebreak()
#half[
*帰納ステップ 2* 長さが $n$ のとき、$overline(w) a in L_A$ とする。$overline(w)$ の長さは $n-1$ である。
帰納法の仮定から $overline(w) in L_W ==> overline(w) in frak(L)(ell_1,bold(L)(slash,backslash), W)$。
文法規則は $A <- W a$ である。$ell_1$ は $ell_1(a) in.rev W backslash A$ とする。
#tree(
myaxi[$[ell_1(overline(w))]=>W$],
myaxi[$A=>A$],
mybin[$[ell_1(overline(w))], W backslash A => A$],
myuni[$[ell_1(overline(w))], [ell_1(a)] => A$],
myuni[$[ell_1( overline(w) a)] => A$]
)
したがって $overline(w) a in frak(L)(ell_1, bold(L)(slash, backslash), A)$ である。
$tack.l$
]
#pagebreak()
*論理 $==>$ 言語*
#half[
*ベースケース*
長さが1で $bold(L)(slash,backslash) tack [ell_1(a)] => A$ \ すなわち $ell_1(a) in.rev A$ である。
このとき、文法規則 を$A <- a$ と置けば $a in L_A$である。
*帰納ステップ* 長さが $n$ のとき文字列 $overline(w)$ を考える。 $[ell_1(overline(w))] => A$ とする。
このとき、推論規則の形から最下段のシーケントは $A slash W, Gamma => A$ もしくは\ $Gamma, W backslash A => A$ のどちらかである。
]
#pagebreak()
#half[
*帰納ステップ1* $A slash W, Gamma => A$ とする。このとき $A => A$ と $ Gamma => W$ の二つに分け分けられる。
文字列が $a overline(w)$ の形をしているなら帰納法の仮定から語彙から $overline(w) in L_W$に関する文法規則 $cal(G)$ を作れてそれに $A <- a W$を加えることができ $a overline(w) in L_A$
]
#pagebreak()
#half[
*帰納ステップ2* $Gamma, W backslash A => A$ とする。このとき $A => A$ と $ Gamma => W$ の二つに分け分けられる。
文字列が $overline(w) a$ の形をしているなら帰納法の仮定から語彙から $overline(w) in L_W$に関する文法規則 $cal(G)$ を作れ、それに $A <- W a$を加えることができ $a overline(w) in L_A$
$tack.l$
したがってどんな文字列 $overline(w)$ に対しても \ $overline(w) in sans(L)_X <==> overline(w) in frak(L)(ell_1, bold(L)(slash,backslash), X)$ である。
]
== 線形文法とランベック計算
#outline-colorbox(title: [定理(言語における導入規則の許容可能性)])[
#v(5pt)
言語 $frak(L)(ell_1,L(slash,backslash), S)$において右導入規則は許容可能である。
#grid(
columns: (200pt,) * 3,
column-gutter: 50pt,
tree(
myaxi[$Sigma, alpha => beta$],
myuni[$Sigma => beta slash alpha$],
),
tree(
myaxi[$alpha,Sigma => beta$],
myuni[$Sigma => alpha backslash beta$],
),
)
つまり、この規則を加えても言語が拡張されることはない。
]
#pagebreak()
#half[
1. $bold(L)(slash,backslash)$ に新たに 右導入規則を加えた\ 普通のランベック計算 $bold(L)$を考える
2. カットフリーの過程のみを考える
3. $overline(s) in frak(L)(ell_1, bold(L), S)$ に対応する証明の最下段$sigma$は $[ell_1(w_1)],dots,[ell_1(w_n)]=> S$
4. $sigma$へ至る証明内での右導入規則を仮定。もっとも下層での右導入規則に注目
5. この右辺を $alpha$ とする。$d(alpha) >= 1$ である
]
#pagebreak()
#half[
6. $alpha$は以下の4つの方法で処理される
1. そのまま残る (3によって棄却される)
2. 右導入規則 (4によって棄却される)
3. カット規則 (2によって棄却される)
4. 左導入規則に用いられる
7. 4の場合を考える。この場合注目している\ 式 $eta$ の次数は $d(alpha) + 1$以上となる。
]
#pagebreak()
#half[
8. $eta$ は以下の4つの方法によって処理される
1. そのまま残る (3によって棄却される)
2. カット規則 (2によって棄却される)
3. 左導入規則
9. 3の場合、その注目した式に 7 の議論へ戻る
10. 9のループでは、次数が単調増加する。\ しかし、これは 2 の仮定に反する。
11. したがって、 4の仮定が棄却される。
]
#pagebreak()
ゆえに $overline(s) in frak(L)(ell_1, bold(L), S)$ において 右導入規則が使われることはなく、\
加えてもその言語が拡張されることはない。つまり $frak(L)(ell_1, bold(L), S) = frak(L)(ell_1, bold(L)(slash, backslash), S)$。\
言語上で右導入規則は許容可能 (addmissible)である。
= ランベック計算と正規文法
#focus-slide[
論理のはなし
]
== ランベック文法の左断片
#outline-colorbox(title: [ランベック計算の左断片 $bold(L)(slash)$])[
#v(5pt)
小文字のアルファベットは原子論理式とする。
小文字のギリシャ文字は式 ($phi := a | phi slash phi | phi backslash phi$) であり大文字のギリシャ文字は式の列である。推論規則は以下。
#grid(
columns: (60pt,150pt,150pt,150pt),
column-gutter: 50pt,
row-gutter: 10pt,
tree(
myaxi[],
myuni[$a => a$]
),
tree(
myaxi[$Gamma,alpha,Delta => beta$],
myaxi[$Sigma => alpha$],
mybin[$Gamma,Sigma,Delta => beta$]
),
tree(
myaxi[$Gamma,alpha,Delta => beta$],
myaxi[$Sigma => gamma$],
mybin[$Gamma,alpha slash gamma, Sigma,Delta => beta$]
),
)
]
#outline-colorbox(title: [カット除去定理(Zielonka 1976)の応用])[
#v(5pt)
$bold(L)(slash) tack Gamma => alpha <==> bold(L)(slash) backslash {"cut"} tack Gamma => alpha$
]
#outline-colorbox(title: [言語のカット除去定理(谷口))])[
#v(5pt)
カット除去定理から次が直ちに導かれる。$frak(L)(ell, bold(L)(slash), S) = frak(L)(ell, bold(L)(slash) backslash {"cut"}, S)$
]
#focus-slide[
言語のはなし
]
== 正規文法
#outline-colorbox(title: "左線形文法")[
#v(5pt)
$A <- a$, $A <- a B$の形で書かれる文法を左線形文法(正規文法)と呼ぶ。\
他の定義もあるが、ここでは標準形として、これを採用する。
]
#outline-colorbox(title: "tips: 右線形文法")[
#v(5pt)
$A <- a$, $A <- B a$の形で書かれる文法を右線形文法(正規文法)と呼ぶ。\
これも正規言語を生成する。
]
#v(-15pt)
== 式の次数と語彙
#outline-colorbox(title: [正規文法とランベック計算の断片(Stepan 2010)])[
#v(5pt)
式のうち演算子 $slash,backslash$ の数を式の次数と呼ぶ。\
語彙 $ell_(1slash)$ は 語彙のうち $slash$のみを含み次数が高々1のものに限定したものとする。\
$sans(L)$ は正規言語とする。このとき $exists ell_(1slash); sans(L) = frak(L)(ell_(1slash), bold(L)(slash), S)$
]
*ランベック計算の左断片と制約された語彙* は正規文法である!
== 正規文法とランベック計算の断片の関係の証明
#outline-colorbox(title: [主張])[
#v(5pt)
言語 $sans(L)_X$ は正規文法で生成される。ルートとなる非終端記号は$X$である。\
このとき $s in L_X <==> s in frak(L)(ell_(1slash),bold(L)(slash), X) $ となる語彙 $ell_(1slash)$が存在する。
]
*言語 $==>$ 論理*
#half[
*ベースケース* 長さが 1のとき$a in L_A$とする。\
このとき対応する文法規則は $A <- a$ である。 \
語彙$ell_(1slash)$ は $ell_(1slash)(a) in.rev A$ とする。\
このとき $s in frak(L)(ell_(1slash), bold(L)(slash), A)$ が成り立つ。
]
#pagebreak()
#half[
*帰納ステップ*
文法規則の形から
$a overline(w) in L_A$に分割される。
$a overline(w) in L_A$ で $overline(w)$ の長さが $n-1$ である。\
仮定から $overline(w) in L_W ==> overline(w) in frak(L)(ell_(1slash),bold(L)(slash), W)$。\
対応する文法規則は $A <- a W$ である。\ $ell_(1slash)$ は $ell_(1slash)(a) in.rev A slash W$ とする。
#tree(
myaxi[$[ell_(1slash)(overline(w))]=>W$],
myaxi[$A=>A$],
mybin[$A slash W, [ell_(1slash)(overline(w))] => A$],
myuni[$[ell_(1slash)(a)], [ell_(1slash)(overline(w))] => A$],
myuni[$[ell_(1slash)(a overline( w))] => A$]
)
したがって $a overline(w) in frak(L)(ell_(1slash), bold(L)(slash), A)$ である。
$tack.l$
]
#pagebreak()
*論理 $==>$ 言語*
#half[
*ベースケース*
長さが1 で $bold(L)(slash) tack [ell_(1slash)(a)] => A$ \ すなわち $ell_(1slash)(a) in.rev A$ である。
このとき、文法規則を $A <- a$ と置けば $a in L_A$である。
]
#pagebreak()
#half[
*帰納ステップ* 長さが $n$ のとき文字列 $overline(w)$ を考える。 $[ell_(1slash)(overline(w))] => A$ とする。
このとき、推論規則の形から最下段のシーケントは $A slash W, Gamma => A$である。
このとき $A => A$ と $ Gamma => W$ の二つに分け分けられる。
文字列が $a overline(w)$ の形であり帰納法の仮定から語彙から $overline(w) in L_W$に関する文法規則 $cal(G)$ を作り、\ $A <- a W$を加えて $a overline(w) in L_A$
$tack.l$
したがってどんな文字列 $overline(w)$ に対しても、\ $overline(w) in sans(L)_X <==> overline(w) in frak(L)(ell_(1slash), bold(L)(slash,backslash), X)$ である。
]
== 正規文法とランベック計算
#outline-colorbox(title: [定理(言語における導入規則の許容可能性)])[
#v(5pt)
言語 $frak(L)(ell_1,L(slash), S)$において以下の導入規則は許容可能である。
#grid(
columns: (200pt,) * 3,
column-gutter: 50pt,
tree(
myaxi[$Gamma,alpha,Delta => beta$],
myaxi[$Sigma => gamma$],
mybin[$Gamma,Sigma,gamma backslash alpha,Delta => beta$]
),
tree(
myaxi[$Sigma, alpha => beta$],
myuni[$Sigma => beta slash alpha$],
),
tree(
myaxi[$alpha,Sigma => beta$],
myuni[$Sigma => alpha backslash beta$],
),
)
つまり、これらの規則を加えても言語が拡張されることはない。
]
#pagebreak()
#half[
1. $bold(L)(slash)$ に新たに 右導入規則を加えた普通のランベック計算 $bold(L)$を考える
2. カットフリーの過程のみを考える
3. $overline(s) in frak(L)(ell_(1slash), bold(L), S)$ に対応する証明の最下段$sigma$は $[ell_(1slash)(w_1)],dots,[ell_(1slash)(w_n)]=> S$
4. $sigma$へ至る証明で $backslash$ の 左導入則を仮定する。
]
#pagebreak()
#half[
5. 続く証明では以下のケースが考えられる
1. そのまま残る (3 によって棄却される)
2. カット規則(2によって棄却される)
3. 左導入規則
6. 3の場合 5の議論を続ける。しかし、次数が単調増加し3によって棄却される
7. よって 4 の仮定は棄却される。
よって、$bold(L)(slash,backslash)$に膨らましても言語は同じ。\
さらに、線形文法と同様の議論で$bold(L)$でも同じ。\
]
== 小まとめ
- ランベック計算 + 無制限の語彙 は 文脈自由文法
- ランベック計算 + 次数 1 の語彙は 線形文法 (New?)
- ランベック計算 + 次数1で$slash$のみの語彙は 正規文法
- ランベック計算 + 次数1で$backslash$のみの語彙は 正規文法 (同様に示せる)
= おまけ: 古典論理への埋め込みがしたいです。
ランベック計算
#grid(
columns: (200pt,) * 3,
column-gutter: 50pt,
tree(
myaxi[],
myuni[$a => a$]
),
tree(
myaxi[$Sigma, alpha => beta$],
myuni[$Sigma => beta slash alpha$],
),
tree(
myaxi[$alpha,Sigma => beta$],
myuni[$Sigma => alpha backslash beta$],
),
tree(
myaxi[$Gamma,alpha,Delta => beta$],
myaxi[$Sigma => alpha$],
mybin[$Gamma,Sigma,Delta => beta$]
),
tree(
myaxi[$Gamma,alpha,Delta => beta$],
myaxi[$Sigma => gamma$],
mybin[$Gamma,alpha slash gamma, Sigma,Delta => beta$]
),
tree(
myaxi[$Gamma,alpha,Delta => beta$],
myaxi[$Sigma => gamma$],
mybin[$Gamma,Sigma,gamma backslash alpha,Delta => beta$]
),
)
ランベック計算の原子論理式に添字を加えると次の同値関係が導かれる (?)
$
exists Delta prec.eq Gamma;bold(L) tack Delta => alpha quad <==> quad "LK" tack bracket.b => [|Gamma => alpha|]
$
$
[|alpha_1,dots,alpha_n=>beta|] := [|alpha_1|]_1 and dots and [|alpha_n|]_n ->[|beta|]_1 or dots or [|beta|]_n \
[|alpha slash beta|]_i := [|beta|]_(i+1) -> [|alpha|]_i quad quad quad
[|alpha backslash beta|]_i := [|alpha|]_(i-1) -> [|beta|]_i quad quad quad
[|a|]_i := a_i
$
= まとめ
- ランベック計算 + 無制限の語彙 は 文脈自由文法
- ランベック計算 + 次数 1 の語彙は 線形文法 (New!)
- ランベック計算 + 次数1で$slash$のみの語彙は 正規文法
- ランベック計算 + 次数1で$backslash$のみの語彙は 正規文法
- ランベック計算を古典論理上でシミュレーションする方法を模索中
|
|
https://github.com/hei-templates/hevs-typsttemplate-thesis | https://raw.githubusercontent.com/hei-templates/hevs-typsttemplate-thesis/main/03-tail/bibliography.typ | typst | MIT License | #import "../00-templates/helpers.typ": *
#pagebreak()
#bibliography("../03-tail/bibliography.bib", style:bibstyle)
|
https://github.com/shealligh/typst-template | https://raw.githubusercontent.com/shealligh/typst-template/main/conf.typ | typst | #let conf(
course: none,
homework: [],
due_time: [],
instructor: [],
student: [],
id: [],
doc
) = {
set text(
font: ("New Computer Modern", "Yuppy SC"),
size: 10pt
)
set page(
paper: "a4",
header: [
#set text(10pt)
#smallcaps[#student]
#h(1fr) #homework
],
numbering: "1 / 1",
background: rotate(45deg,
text(80pt, fill: rgb("fde7e4"))[
#student
]
)
)
set align(center)
text(22pt, weight: "bold", [
#course: #homework
])
align(center, text(12pt, [
Instructed by #text(style: "italic", instructor)
]))
align(center, text(10pt, [
Due on #text(style: "italic", due_time)
]))
align(center, text(14pt, [
\ #student #h(1cm) #id
]))
set par(justify: true)
set align(left)
show math.equation.where(block: false): it => {
if it.has("label") and it.label == label("displayed-inline-math-equation") {
it
} else {
[$display(it)$<displayed-inline-math-equation>]
}
}
show raw.where(block: true): block.with(
fill: luma(200, 40%),
inset: 10pt,
radius: 4pt,
)
doc
}
#let prob = counter("problem")
#let problem(name: none, content) = {
prob.step()
if name != none {
align(left, text(16pt, weight: "bold")[#name])
}
else {
align(left, text(16pt, weight: "bold")[Problem #prob.display()])
}
align(left, content)
}
#let blockquote(content) = {
rect(fill: luma(94.12%), stroke: (left: 0.25em))[
#content
]
}
#let proof(content) = {
block(
fill: rgb("#c5e5fc6f"),
radius: 4pt,
inset: 8pt
)[
#text(style: "italic", [
Proof.
])
#content
#h(1fr) $square.stroked$
]
}
#let theo = counter("theorem")
#let theorem(name: none, content) = {
theo.step()
if name != none {
name = text[(#name)]
}
rect(fill: rgb("#eeffee"))[
#text(weight: "bold")[Theorem #theo.display()]
#text[#name. #content]
]
}
#let ans(content) = {
block(
fill: rgb("#d0edcb6f"),
radius: 4pt,
inset: 8pt,
width: 100%
)[
#text(style: "italic", [
Answer.
])
#content
]
}
// Code from https://typst-doc-cn.github.io/docs/chinese/
#let skew(angle, vscale: 1, body) = {
let (a, b, c, d) = (1, vscale * calc.tan(angle), 0, vscale)
let E = (a + d) / 2
let F = (a - d) / 2
let G = (b + c) / 2
let H = (c - b) / 2
let Q = calc.sqrt(E * E + H * H)
let R = calc.sqrt(F * F + G * G)
let sx = Q + R
let sy = Q - R
let a1 = calc.atan2(F, G)
let a2 = calc.atan2(E, H)
let theta = (a2 - a1) / 2
let phi = (a2 + a1) / 2
set rotate(origin: bottom + center)
set scale(origin: bottom + center)
rotate(phi, scale(x: sx * 100%, y: sy * 100%, rotate(theta, body)))
}
#let fake-italic(body) = skew(-12deg, body)
#let shadowed(body) = box(place(skew(-50deg, vscale: 0.8, text(fill: luma(200), body))) + place(body)) // TODO: fix shadowed 错位问题 |
|
https://github.com/Gewi413/typst-autodoc | https://raw.githubusercontent.com/Gewi413/typst-autodoc/master/typst-autodoc.typ | typst | MIT License | /**
* splits and filters the file into function headers with magic \/\*\*\
* @param text the text which is to get parsed
* @returns List of all functions with a docstring as plaintext
*/
#let findDocs(text) = {
let docComment = false
let function = false
let buff = ""
let headers = ()
for line in text.split("\n") {
if line.starts-with("/**") {
buff = ""
docComment = true
}
if docComment {
buff += line + "\n"
if "*/" in line {
docComment = false
function = true
}
}
if function {
buff += line + " "
if ")" in line {
headers.push(buff)
buff = ""
function = false
}
}
}
return headers
}
/**
* makes a red error box
* @param message the message to error with
* @foo
*/
#let error(message: "error") = box(fill: red, inset: 5pt, [#message])
/**
* parses a docstring and functionhead into a dictonary
* @returns dictionary with keys name, params, see-also, description, errors, version
*/
#let parseDocs(text) = {
let info = (
name: "",
params:(:),
see-also: (),
description: "",
errors: (),
version: "",
returns: "",
)
let lines = text.split("\n")
let head = lines.at(-1)
let name = if ")" in head {
head.matches(regex("let ([^(]+)"))
} else {
head.matches(regex("let ([^ ]+)"))
}.at(0).captures.at(0)
info.name = name
let params = (:)
for line in lines.slice(0,-1) {
let line = line.trim(regex("[ */]"))
let onward = line.split(" ").slice(1,)
let firstArg = onward.at(0, default: "")
if "@" not in line {
info.description += line + "\n"
} else if line.starts-with("@param") {
if onward.len() > 1 {
params.insert(firstArg, onward.slice(1,).join(" "))
}
} else if line.starts-with("@returns") {
info.returns = onward.join(" ")
} else if line.starts-with("@see") {
info.see-also += (firstArg,)
} else if line.starts-with("@version") {
info.insert("version", onward.join(" "))
} else {
info.errors += (line.split(" ").at(0),)
}
}
let args = head.slice(head.position("(") + 1, head.position(")")).split(",")
if args != () {
for arg in args {
let name = arg.split(":").at(0).trim()
info.params.insert(name, (:))
let default = arg.split(":").at(1, default: none)
if default != none {
info.params.at(name).default = default.trim()
}
if name in params {
info.params.at(name).description = params.at(name)
}
}
}
info.description = info.description.trim()
return info
}
/**
* prints the documentation
* == Feature
* can include _inline_ typst for more (rocket-emoji)
* @version 0.1.1
* @param file The file to parse into a documentation
* @returns Content filled with blocks for each function
* @see parseDocs
*/
#let main(file) = {
show heading.where(level: 2): set text(fill: gray, size: 11pt)
set text(font: "Fira Sans")
let headers = findDocs(read(file))
for function in headers {
block(breakable: false, box(fill: gray.lighten(80%), width: 100%, inset: 5pt, {
let info = parseDocs(function)
[= #info.name #label(info.name)
#if info.version != "" [
#h(2em) Version: #info.version
]
#eval("[" + info.description + " ]")
#if info.params != (:) [
== Parameters
#for (name, param) in info.params [
/ #raw(name): #param.at("description", default: "") #if "default" in param [
(default value: #raw(param.default))
]
]
]
#if info.returns != "" [
== Return value
#info.returns
]
#if info.see-also != () {
[== See also]
for other in info.see-also [
- #link(label(other), other)
]
}
#if info.errors != () {
[== Parsing errors]
for e in info.errors {
error(message: e)
}
}
]
}))
}
}
|
https://github.com/loqusion/typix | https://raw.githubusercontent.com/loqusion/typix/main/examples/quick-start/main.typ | typst | MIT License | = Lorem ipsum
#lorem(30)
|
https://github.com/hewliyang/fyp-typst | https://raw.githubusercontent.com/hewliyang/fyp-typst/main/main.typ | typst | #set par(justify: true, linebreaks: auto)
#set text(font: "New Computer Modern", size: 12pt)
#set page(paper: "a4", margin: (x: 1in, y: 1in))
#set figure(gap: 12pt)
#set math.equation(numbering: "(1)", supplement: [Equation])
#show heading: it => {
it
v(1em)
}
#show link: box.with(stroke: 1pt + blue, outset: (bottom: 1.5pt, x: .5pt, y: .5pt))
#show cite: box.with(stroke: 1pt + green, outset: (bottom: 1.5pt, x: .5pt, y: .5pt))
#show ref: box.with(stroke: 1pt + red, outset: (bottom: 1.5pt, x: .5pt, y: .5pt))
#let newPage = pagebreak
#include "front-page.typ"
#newPage()
#outline(title: "Table of Contents", depth: 999, indent: true)
#newPage()
#include "abstract.typ"
#newPage()
#set page(numbering: "1", header: align(right)[Evaluating Synthetic Speech])
#include "intro.typ"
#newPage()
#include "preliminaries.typ"
#newPage()
#include "related-work.typ"
#newPage()
#include "dataset-curation.typ"
#newPage()
#include "ablations.typ"
#newPage()
#include "self-supervised.typ"
#newPage()
#include "conclusion.typ"
#newPage()
#bibliography("references.bib", style: "springer-basic-author-date")
#newPage()
#outline(title: "Tables", target: figure.where(kind: table))
#newPage()
#outline(title: "Images", target: figure.where(kind: image)) |
|
https://github.com/SabrinaJewson/cmarker.typ | https://raw.githubusercontent.com/SabrinaJewson/cmarker.typ/main/examples/tests.md | markdown | MIT License | Tests
=====
This document contains a bunch of tests that should be manually checked.
(This should be on the same line) (as this)
(This should be above)
(this)
Basic styling: *italics*, _italics_, **bold**, __bold__, ~strikethrough~
Unlike Typst, bare links are not clickable: https://example.org.
Angle-bracket links are clickable: <https://example.org>.
We can also use links with text: [example.org](https://example.org).
Unlike Typst, we cannot do references with an at sign: @reference.
## Heading 2
### Heading 3
#### Heading 4
##### Heading 5
###### Heading 6
code block defined through indentation (no syntax highlighting)
We can put triple-backticks in indented code blocks:
```rust
let x = 5;
```
```rust
// Code block defined through backticks, with syntax highlighting
```
Some `inline code`.
A horizontal rule:
---
- an
- unordered
- list
Inline math: $\int_1^2 x \mathrm{d} x$
Display math:
$$
\int_1^2 x \mathrm{d} x
$$
with this paragraph nested in the last list element
We can escape things with backslashes:
\*asterisks\*,
\`backticks\`,
\_underscores\_,
\# hashes,
\~tildes\~,
\- minus signs,
\+ plus signs,
\<angle brackets\>.
== Putting equals signs at the start of the line does not make this line into a heading.
/ Unlike Typst, this line is plain text: and not a term and definition
Similarly, math mode does not work: $ x = 5 $
A backslash on its own does not produce a line break: a\b.
Typst commands do not work: #rect(width: 1cm)
Neither do Typst comments: /* A comment */ // Line comment
Neither does tildes: foo~bar
Neither do Unicode escapes: \u{1f600}
Smart quotes: 'smart quote' "smart quote"
We can escape them to make not-smart quotes: \'not smart quote\' \"not smart quote\"
We have Markdown smart punctuation, such as en dashes (-- and –) and em dashes (--- and —).
> Quoted text
>
> > Nested
>
> Unnnested
<!--typst-begin-exclude-->
This should not appear.<!--typst-end-exclude-->
Raw Typst code:
<!--raw-typst $ 2 + 2 = #(2 + 2) $-->
|
https://github.com/TypstApp-team/typst | https://raw.githubusercontent.com/TypstApp-team/typst/master/tests/typ/meta/footnote-break.typ | typst | Apache License 2.0 | // Test footnotes that break across pages.
---
#set page(height: 200pt)
#lorem(5)
#footnote[ // 1
A simple footnote.
#footnote[Well, not that simple ...] // 2
]
#lorem(15)
#footnote[Another footnote: #lorem(30)] // 3
#lorem(15)
#footnote[My fourth footnote: #lorem(50)] // 4
#lorem(15)
#footnote[And a final footnote.] // 5
|
https://github.com/daskol/typst-templates | https://raw.githubusercontent.com/daskol/typst-templates/main/tmlr/README.md | markdown | MIT License | # Transactions on Machine Learning Research (TMLR)
## Usage
You can use this template in the Typst web app by clicking _Start from
template_ on the dashboard and searching for `healthy-tmlr`.
Alternatively, you can use the CLI to kick this project off using the command
```shell
typst init @preview/smooth-tmlr
```
Typst will create a new directory with all the files needed to get you started.
## Example Papers
Here are an example paper in [LaTeX][1] and in [Typst][2].
## Configuration
This template exports the `tmlr` function with the following named arguments.
- `title`: The paper's title as content.
- `authors`: An array of author dictionaries. Each of the author dictionaries
must have a name key and can have the keys department, organization,
location, and email.
- `keywords`: Publication keywords (used in PDF metadata).
- `date`: Creation date (used in PDF metadata).
- `abstract`: The content of a brief summary of the paper or none. Appears at
the top under the title.
- `bibliography`: The result of a call to the bibliography function or none.
The function also accepts a single, positional argument for the body of the
paper.
- `appendix`: Content to append after bibliography section.
- `accepted`: If this is set to `false` then anonymized ready for submission
document is produced; `accepted: true` produces camera-redy version. If
the argument is set to `none` then preprint version is produced (can be
uploaded to arXiv).
- `review`: Hypertext link to review on OpenReview.
- `pubdate`: Date of publication (used only month and date).
The template will initialize your package with a sample call to the `tmlr`
function in a show rule. If you want to change an existing project to use this
template, you can add a show rule at the top of your file.
## Issues
- While author instruction says the all text should be in sans serif font
Computer Modern Bright, only headers and titles are in sans font Computer
Modern Sans and the rest of text is causal Computer Modern Serif (or Roman).
To be precice, the original template uses Latin Modern, a descendant of
Computer Modern. In this tempalte we stick to CMU (Computer Modern Unicode)
font family.
- In the original template paper, the word **Abstract** is of large font size
(12pt) and bold. This affects slightly line spacing. We don't know how to
adjust Typst to reproduce this feature of the reference template but this
issue does not impact a lot on visual appearence and layouting.
- In the original template special level-3 sections like "Author Contributions"
or "Acknowledgements" are not added to outline. We add them to outline as
level-1 header but still render them as level-3 headers.
- ICML-like bibliography style. In this case, the bibliography slightly differs
from the one in the original example paper. The main difference is that we
prefer to use author's lastname at first place to search an entry faster.
- In the original template a lot of vertical space is inserted before and after
graphics and table figures. It is unclear why so much space are inserted. We
belive that the reason is how Typst justify content verticaly. Nevertheless,
we append a page break after "Default Notation" section in order to show that
spacing does not differ visually.
- Another issue is related to Typst's inablity to produce colored annotation.
In order to mitigte the issue, we add a script which modifies annotations and
make them colored.
```shell
../colorize-annotations.py \
example-paper.typst.pdf example-paper-colored.typst.pdf
```
See [README.md][3] for details.
[1]: example-paper.latex.pdf
[2]: example-paper.typst.pdf
[3]: ../#colored-annotations
|
https://github.com/augustebaum/epfl-thesis-typst | https://raw.githubusercontent.com/augustebaum/epfl-thesis-typst/main/src/lib.typ | typst | MIT License | #let fill-line(left-text, right-text) = [#left-text #h(1fr) #right-text]
// The `in-outline` mechanism is for showing a short caption in the list of figures
// See https://sitandr.github.io/typst-examples-book/book/snippets/chapters/outlines.html#long-and-short-captions-for-the-outline
#let in-outline = state("in-outline", false)
#let flex-caption(long, short) = context { if in-outline.get() { short } else {
long } }
// ---
#let front-matter(body) = {
set page(numbering: "i")
counter(page).update(1)
set heading(numbering: none)
show heading.where(level: 1): it => {
it
v(6%, weak: true)
}
body
}
#let main-matter(body) = {
set page(numbering: "1")
counter(page).update(1)
counter(heading).update(0)
set heading(numbering: "1.1")
show heading.where(level: 1): it => {
it
v(12%, weak: true)
}
body
}
#let back-matter(body) = {
set heading(numbering: "A", supplement: [Appendix])
// Without this, the header says "Chapter F"
counter(heading.where(level: 1)).update(0)
// Without this, the table of contents line says "Chapter F"
counter(heading).update(0)
body
}
// ---
// This function gets your whole document as its `body` and formats it
#let template(
// The title for your work.
title: [Your Title],
// Author's name.
author: "Author",
// The paper size to use.
paper-size: "a4",
// Date that will be displayed on cover page.
// The value needs to be of the 'datetime' type.
// More info: https://typst.app/docs/reference/foundations/datetime/
// Example: datetime(year: 2024, month: 03, day: 17)
date: none,
// Format in which the date will be displayed on cover page.
// More info: https://typst.app/docs/reference/foundations/datetime/#format
date-format: "[month repr:long] [day padding:zero], [year repr:full]",
// The content of your work.
body,
) = {
// Set the document's metadata.
set document(
title: title, author: author, date: if date != none { date } else { auto },
)
// Set the body font.
set text(font: ("Utopia LaTeX"), size: 11pt)
// Configure page size and margins.
set page(
paper: paper-size, margin: (
bottom: 5cm, top: 4cm,
// The original LaTeX template references something called "hoffset", not sure what that is yet
inside: 26.2mm, outside: 37mm,
), numbering: "1", number-align: right,
)
// Configure paragraph properties.
// Default leading is 0.65em.
set par(leading: 0.7em, justify: true, linebreaks: "optimized")
// Default spacing is 1.2em.
show par: set block(spacing: 1.35em)
show heading: it => {
v(2.5em, weak: true)
it
v(1.5em, weak: true)
}
// Style chapter headings.
show heading.where(level: 1): it => {
set text(size: 22pt)
// Has no effect, still shows "Section"
set heading(supplement: [Chapter])
let black_rectangle = place(
dx: -page.margin.outside, dy: -1em, rect(fill: black, width: page.margin.outside - 5pt, height: 2em),
)
let heading_number = if heading.numbering == none { [] } else { counter(heading.where(level: 1)).display() }
let white_heading_number = place(dx: -1em, text(fill: white, heading_number))
// Start chapters on even pages
// FIXME: `pagebreak(to: "even")` replicates the behaviour seen in the
// original template, except for an important detail: the resulting empty
// pages still show the header and page number. This is not great and is the
// subject of https://github.com/typst/typst/issues/2722.
// pagebreak(to: "even")
pagebreak()
v(16%)
rect(
stroke: none, inset: 0em, black_rectangle + white_heading_number + it.body,
)
}
// Configure heading numbering.
set heading(numbering: "1.1")
// Do not hyphenate headings.
show heading: set text(hyphenate: false)
// Set page header
set page(
header-ascent: 30%, header: context{
// Get current page number.
let page-number = here().page()
// [ #repr(query(<disable_header>).map(el => el.location().page()).slice(0, 5)) ]
// If the current page is the start of a chapter, don't show a header
let target = heading.where(level: 1)
if query(target).any(it => it.location().page() == page-number) {
// return [New chapter! page #here().page(), #i]
return []
}
// Find the chapter of the section we are currently in.
let before = query(target.before(here()))
if before.len() > 0 {
let current = before.last()
let chapter-title = current.body
let chapter-number = counter(heading.where(level: 1)).display()
// let chapter-number-text = [#current.supplement Chapter #chapter-number]
let chapter-number-text = [Chapter #chapter-number]
if current.numbering != none {
let (left-text, right-text) = if calc.odd(page-number) {
(chapter-number-text, chapter-title)
} else {
(chapter-title, chapter-number-text)
}
text(weight: "bold", fill-line(left-text, right-text))
v(-1em)
line(length: 100%, stroke: 0.5pt)
}
}
},
)
// The `in-outline` is for showing a short caption in the list of figures
// See https://sitandr.github.io/typst-examples-book/book/snippets/chapters/outlines.html#long-and-short-captions-for-the-outline
show outline: it => {
in-outline.update(true)
// Show table of contents, list of figures, list of tables, etc. in the table of contents
set heading(outlined: true)
it
in-outline.update(false)
}
// Indent nested entries in the outline.
set outline(indent: auto, fill: repeat([#h(2.5pt) . #h(2.5pt)]))
show outline.entry: it => {
// Only apply styling if we're in the table of contents (not list of figures or list of tables, etc.)
if it.element.func() == heading {
if it.level == 1 {
v(1.5em, weak: true)
strong(it)
} else {
it
}
} else {
it
}
}
// Configure equation numbering.
set math.equation(numbering: n => {
let h1 = counter(heading).get().first()
numbering("(1.1)", h1, n)
})
show math.equation.where(block: true): it => {
set align(left)
// Indent
pad(left: 2em, it)
}
// FIXME: Has no effect?
set place(clearance: 2em)
set figure(numbering: n => {
let h1 = counter(heading).get().first()
numbering("1.1", h1, n)
}, gap: 1.5em)
set figure.caption(separator: [ -- ])
show figure.caption: it =>{
if it.kind == table {
align(center, it)
} else {
align(left, it)
}
}
show figure.where(kind: table): it => {
set figure.caption(position: top)
// Break large tables across pages.
set block(breakable: true)
it
}
set table(stroke: none)
// Set raw text font.
show raw: set text(font: ("Iosevka", "Fira Mono"), size: 9pt)
// Display inline code in a small box that retains the correct baseline.
// show raw.where(block: false): box.with(
// fill: luma(250).darken(2%), inset: (x: 3pt, y: 0pt), outset: (y: 3pt), radius: 2pt,
// )
// Display block code with padding.
show raw.where(block: true): block.with(inset: (x: 5pt))
// Show a small maroon circle next to external links.
show link: it => {
// Workaround for ctheorems package so that its labels keep the default link styling.
if type(it.dest) == label { return it }
it
h(1.6pt)
super(
box(height: 3.8pt, circle(radius: 1.2pt, stroke: 0.7pt + rgb("#993333"))),
)
}
body
}
|
https://github.com/Greacko/typyst_library | https://raw.githubusercontent.com/Greacko/typyst_library/main/library/title_page.typ | typst | #let title_page(title, prof, season) = {
set document(title: title, author: "<NAME>")
align(grid(text(title, top-edge:10em, size: 22pt),
text(season, top-edge:1.5em, size:20pt),
text("Prof: " + prof, top-edge:4em, size:18pt),
text("<NAME>",top-edge:1.5em, size:16pt), columns: auto),center)
}
#let hw_page(title, class, prof, season) = {
set document(title: title, author: "<NAME>")
align(grid(
text(title, top-edge:10em, size: 22pt),
text(class, top-edge:7em, size: 18pt),
text(season, top-edge:1.5em, size:17pt),
text("Prof: " + prof, top-edge:4em, size:16pt),
text("<NAME>",top-edge:1.5em, size:16pt), columns: auto),center)
} |
|
https://github.com/dantevi-other/kththesis-typst | https://raw.githubusercontent.com/dantevi-other/kththesis-typst/main/utils/styles.typ | typst | MIT License | /* ---------------------------------------------
This file conatains functions containing style
rules and that are meant to be used with the
`#show` rule to either set the styles to the rest
of the contents in a file or to a specified
element in a file.
Example:
```typ
#import "utils/styles.typ" as styles
// This applies the styles set by the function to
// the rest of the content succeding the statement
#show: rest => styles.set-base-typography-styles(rest)
```
--------------------------------------------- */
//-- Imports
#import "values.typ" as values
//-- Base typography
#let set-base-typography-styles(it) = {
set text(
font: "New Computer Modern",
size: values.font-size-base
)
it
}
//-- Headings
/*
TODO:
- Headings need to be styled.
*/
//-- Headers
/*
TODO:
- Dynamic headers need to be implemented.
*/
//-- Page numbering
/*
TODO:
- Page numbering formatting needs to be automatically changed for when the
pages contain a chapter heading (i.e., a heading defined with `=`).
*/
//-- Outline formatting
/*
TODO:
- The outline needs to be formatted (i.e., the Table of Contents). For
example, the level 1 headings (i.e., chapter headings) need to be
formatted so that they are bolded and so that the abstract sections are not included.
*/ |
https://github.com/Myriad-Dreamin/tinymist | https://raw.githubusercontent.com/Myriad-Dreamin/tinymist/main/crates/tinymist-query/src/fixtures/semantic_tokens/heading.typ | typst | Apache License 2.0 | === #text("Text in heading") |
https://github.com/EpicEricEE/typst-plugins | https://raw.githubusercontent.com/EpicEricEE/typst-plugins/master/hash/src/lib.typ | typst | #import "hash.typ": hash, hex, blake2, blake2s, md5, sha1, sha224, sha256, sha384, sha512, sha3
|
|
https://github.com/sora0116/unix_seminar | https://raw.githubusercontent.com/sora0116/unix_seminar/master/presentation/main.typ | typst | #import "template.typ": *
#show: my-theme.with(
title: "第10回Unixゼミ",
author: "<NAME>",
date: datetime(year: 2024, month: 7, day: 13),
)
#show raw: it => {
if it.lang == "shell" {
if it.block {
block(
fill: rgb("#1d2433"),
inset: 15pt,
radius: 5pt,
width: 100%,
text(fill: colors.at(0), it),
below: 10pt
)
} else {
box(
fill: rgb("#1d2433"),
inset: 15pt,
radius: 5pt,
width: 1fr,
text(fill: colors.at(0), it)
)
}
} else {
it
}
}
#set heading(numbering: "1.1")
#title-slide(title: [第10回Unixゼミ\ Cプログラム(デバッグ編)], author: "川島研 B4 高木 空")[
]
= はじめに
#slide(title: "はじめに")[
- 演習でGCC、GDB、LLDB、Perfを使用します。
```shell
$ gcc --version
$ gdb --version
$ lldb --version
$ perf --version
```
を打って入っているか確認してください。
]
#slide(title: "入れ方")[
- GCC、GDB、LLDB
```shell
$ sudo apt install gcc
$ sudo apt install gdb
$ sudo apt install lldb
```
- perf (Ubuntu)
```shell
$ sudo apt install linux-tools-$(uname -r) linux-tools-generic linux-tools-common
```
]
#slide(title: "内容")[
- デバッガ
- GDB
- LLDB
- プロファイラ
- Perf
- 演習やスライド、資料等
- Github: https://github.com/sora0116/unix_seminar
- CloneでもDownload ZIPでも
]
= デバッガ
== デバッガとは
=== 概要
#slide(title: "デバッガ")[
- デバッグ (debug)
- バグ(bug)を取り除く(de-)こと
- デバッグの手法
- printデバッグ
- コードを読む
- デバッガを使う
- 今回の主題
]
== デバッグの手法
=== printデバッグ
#slide(title: "デバッグの手法")[
- printデバッグ
- ソースコードにprintを埋め込む
- 利点
- 気軽に実行できる
- 欲しい出力を欲しい形式で得られる
- 欠点
- ソースコードを改変する必要がある
- バグの箇所を検討してからしかできない
- 得られる情報が少ない
]
=== デバッガ
#slide(title: "デバッグの手法")[
- デバッガを使う
- デバッガ - デバッグを補助するツール
- 利点
- プログラム全体を観察できる
- プログラムの変更が(一般には)不要
- スタックやメモリの監視もできる
- 欠点
- 使い方を知っている必要がある
]
== デバッガの具体例
=== GDBとLLDB
#slide(title: "C言語のデバッガ")[
- C言語プログラムのデバッガ
- GDB
- Gnu Projectのデバッガ
- gccを使うならコレ
- Linuxに標準搭載されている
- LLDB
- LLVMのデバッガ
- clangを使うならコレ
]
= GDB
== GDBの起動、終了
=== 起動
#slide(title: "GDBの起動")[
```shell
$ gdb [options] [<program>]
```
でGDBを起動
- `options` : 起動時のオプションを指定
- `--help` : 簡単な使い方を表示
- `--tui` : TUIモード(後述)で起動
- `program` : デバッグ対象の実行可能ファイルを指定
]
=== 終了
#slide(title: "GDBの終了")[
- GDBが起動すると先頭に`(gdb)`と表示される
```shell
(gdb) quit [<expr>]
(gdb) exit [<expr>]
```
でGDBを終了(`ctrl-d`でも可)
引数:
- `expr` : GDBの終了コードを指定
]
=== シェルコマンド
#slide(title: "GDB起動中のシェルコマンド")[
```shell
(gdb) shell <command>
(gdb) ! <command>
```
でGDB起動中にシェルコマンドを実行
引数:
- `command` : 実行するシェルコマンド
補足:
- パイプ等も使える
]
== コマンド
=== コマンド概要
#slide(title: "コマンド概要")[
- GDBはコマンドで操作
- `quit`や`shell`もコマンド
```shell
(gdb) <command> [<args>...]
```
の形で入力
- コマンドが区別できれば省略できる
- 例 : `quit` $arrow$ `q`
- `TAB`キーによる補完が可能
- 候補が唯一の場合自動入力
- 複数の場合2回押すと候補を表示
]
=== ヘルプ
#slide(title: "コマンド補助")[
```shell
(gdb) help [<class>|<command>]
```
コマンドの一覧や使い方を表示
引数:
- `class` : コマンド群を指定するクラス
- `command` : ヘルプを見たいコマンドを指定
補足:
- 引数無しで`help`を実行すると`class`の一覧が表示される
]
== プログラムの開始
=== スタート
#slide(title: "プログラムの開始")[
```shell
(gdb) run [<args>...]
```
でプログラムをGDBの下で実行
- `args` : プログラムのコマンドライン引数として渡される
]
=== チェックポイントとリスタート
#slide(title: "チェックポイントとリスタート")[
特定の場所でのプログラムの状態を保存して再開できる
```shell
(gdb) checkpoint
```
で現在の状態を保存
```shell
(gdb) info checkpoints
```
で保存したチェックポイントの一覧を表示
```shell
(gdb) restart <id>
```
で指定したチェックポイントから再開
]
== プログラムの停止
=== プログラム中断の概要
#slide(title: "プログラムの停止")[
- GDBを使うとプログラムを中断できる
- 停止する条件
- ブレークポイント
- ウォッチポイント
- キャッチポイント
- 実行の再開
- 継続実行
- ステップ実行
]
=== ブレークポイント
#slide(title: "ブレークポイント")[
- プログラム上の指定場所に到達したら中断
```shell
(gdb) break [<loc>] [if <cond>]
```
でブレークポイントを設置
引数:
- `loc` : 位置指定。以下の形式で指定:
- `[<filename>:]<linenum>` : 行番号指定
- `<offset>` : 行オフセット指定
- `[<filename>:]<function>` : 関数名指定
- `cond` : 条件式。満たすときだけ中断
]
=== ウォッチポイント
#slide(title: "ウォッチポイント")[
式の値が変更したら中断
```shell
(gdb) watch [-location] <expr>
```
でウォッチポイントを設置
引数:
- `-location` : `expr`の参照するメモリを監視
- `expr` : 監視対象の式
]
=== ブレークポイントの削除
#slide(title: "ブレークポイントの削除")[
```shell
(gdb) clear [<locspec>]
```
`<locspec>`にあるブレークポイントを削除
```shell
(gdb) delete [breakpoints] [<list>...]
```
`<list>`で指定したブレークポイント、ウォッチポイントを削除
```shell
(gdb) info breakpoints
```
設置されたブレークポイント、ウォッチポイントを表示
]
== プログラムの再開
=== 継続実行
#slide(title: "継続実行")[
次の停止場所まで実行する
```shell
(gdb) continue [<count>]
(gdb) fg [<count>]
```
で継続実行
引数:
- `count` : 停止箇所を無視する回数
]
=== ステップ実行
#slide(title: "ステップ実行")[
次の停止箇所を指定しつつ再開
```shell
(gdb) step [<count>]
(gdb) nexti [<count>]
```
で次の行まで実行。
補足:
- `step`は関数呼び出しの場合中に入る
- `next`は関数呼び出しの場合中に入らない
引数:
- `count` : 無視する行数
```shell
(gdb) until <locspec>
```
`locspec`で指定した位置まで実行
]
== スタックの調査
=== バックトレース
#slide(title: "バックトレース")[
関数呼び出しのトレース
```shell
(gdb) backtrace
(gdb) where
(gdb) info stack
```
でバックトレースを表示
]
=== フレームの選択
#slide(title: "フレームの選択")[
```shell
(gdb) frame [<spec>]
```
でフレームを選択
引数:
- `spec`: フレームを指定。以下の形式が可能
- `<num>` : フレーム番号を指定
- `<function-name>` : 関数名を指定
```shell
up <n>
down <n>
```
で一つ上または下のフレームを指定
]
=== フレーム関連のステップ実行
#slide(title: "ステップ実行")[
```shell
(gdb) finish
```
で選択中のフレームが返るまで実行
]
== ソースコードの調査
=== リスト
#slide(title: "ソースコード情報の表示")[
```shell
(gdb) list [<line>|<function>|+|-]
```
でソースコードを表示
引数:
- `line` : 行番号を指定してそこを中心に表示
- `function` : 関数名を指定して開始地点を中心に表示
- `+`, `-` : 前に表示した部分の後/前を表示
```shell
(gdb) list <start>, <end>
```
で指定部分を表示
]
== データの調査
=== プリント
#slide(title: "プリント")[
```shell
(gdb) print [[<options>...] --] [/<fmt>] <expr>
```
でフォーマットを指定して`expr`の値を表示
引数:
- `options` : オプション
- `fmt` : フォーマット指定。以下が指定可能:
- `x, d, u, o, t, z`: 16,10,符号なし10,8,2,0埋め16進数で表示
- `a`: アドレスとして表示
- `c`: 整数にキャストして文字として表示
- `f`: 浮動小数として表示
- `s`: 文字列として表示
- `r`: 生フォーマットで表示
- `expr` : 表示する値
]
#slide(title: "メモリ")[
```shell
(gdb) x[/<num><fmt><unit>] <addr>
```
でメモリの内容を表示
引数:
- `num`: 表示するメモリ量(単位: `unit`)
- `fmt`: フォーマット指定。以下が指定可能:
- `print`で指定可能なフォーマット
- `i`: 機械語命令として表示
- `m`: メモリタグとして表示
- `unit`: `num`で使用する単位
- `b, h, w, g`: 1, 2, 4, 8バイト
- `addr`: 表示するメモリ領域の先頭アドレス
]
=== ディスプレイ
#slide(title: "ディスプレイ")[
```shell
(gdb) display[/<fmt>] <expr>
```
でプログラムが停止する度に自動で表示
フォーマットに応じて`print`か`x`が呼ばれる
引数:
- `fmt`: フォーマットを指定。`print`,`x`で指定可能なものが指定可能
- `expr`: 表示する式またはアドレス
```shell
(gdb) info display
```
で設定されているディスプレイのリストを表示
```shell
(gdb) undisplay <dnum>...
```
でディスプレイを解除
]
=== 人工配列
#slide(title: "人工配列")[
```shell
(gdb) p <first>@<len>
```
で`first`を最初の要素とする長さ`len`の配列として表示
例:
```c
int *arr = (int*)malloc(2 * sizeof(int));
```
と宣言したものを
```shell
(gdb) p *arr@2
```
で表示
```shell
(gdb) p (int[2])*arr
```
でも可
]
=== レジスタ
#slide(title: "レジスタ")[
```shell
(gdb) info registers
```
でベクタ、フロート以外のレジスタを全て表示
```shell
(gdb) info all-registers
```
ですべてのレジスタを表示
]
== (トレースポイント)
== (TUI)
== 演習1
#slide(title: "演習1")[
#align(center+horizon)[演習1を解いてください。]
]
= LLDB
== LLDBの起動、終了
=== 起動
#slide(title: "LLDBの起動")[
```shell
$ lldb [<options>]
```
でLLDBを起動
]
=== 終了
#slide(title: "LLDBの終了")[
- GDBが起動すると先頭に`(lldb)`と表示される
```shell
(lldb) quit [<expr>]
(lldb) exit [<expr>]
```
でLLDBを終了(`ctrl-d`でも可)
引数:
- `expr` : LLDBの終了コードを指定
]
== コマンド
=== コマンド概要
#slide(title: "コマンド概要")[
- LLDBはコマンドで操作
- `quit`や`shell`もコマンド
```shell
(lldb) <noun> <verb> [-<option> [<option-value>]] [<args>]
```
の形で入力
- コマンドが区別できれば省略できる
- 例 : `quit` $arrow$ `q`
- `TAB`キーによる補完が可能
- 候補が唯一の場合自動入力
- 複数の場合2回押すと候補を表示
]
=== ヘルプ
#slide(title: "コマンド補助")[
```shell
(lldb) help <command>
```
コマンドの一覧や使い方を表示
引数:
- `command` : ヘルプを見たいコマンドを指定
補足:
- 引数無しで`help`を実行すると`command`の一覧が表示される
]
== プログラムの開始
=== スタート
#slide(title: "プログラムの開始")[
```shell
(gdb) process launch [<options>] [<args>]
```
でプログラムをLLDBの下で実行
- `args` : プログラムのコマンドライン引数として渡される
`options`:
- `-s`: エントリポイントで停止
]
== プログラムの停止
=== プログラム中断の概要
#slide(title: "プログラムの停止")[
- LLDBを使うとプログラムを中断できる
- 停止する条件
- ブレークポイント
- ウォッチポイント
- 実行の再開
- 継続実行
- ステップ実行
]
=== ブレークポイント
#slide(title: "ブレークポイント")[
- プログラム上の指定場所に到達したら中断
```shell
(gdb) breakpoint set [<options>]
```
でブレークポイントを設置
`options`:
- `-l <num>`: 行番号を指定
- `-n <name>`: 関数名を指定
- `-E <lang>`: 例外を指定
]
=== ウォッチポイント
#slide(title: "ウォッチポイント")[
式の値が変更したら中断
```shell
(gdb) watchpoint set expression [<options>] <expr>
(gdb) watchpoint set variable [<options>] <varname>
```
でウォッチポイントを設置
`options`:
- `-w`: ウォッチタイプを指定
- `read`: 読まれたら停止
- `write`: 書かれたら停止
- `read_write`: 読み書きがあったら停止
]
=== ブレークポイントの削除
#slide(title: "ブレークポイントの削除")[
```shell
(gdb) breakpoint delete [<options>] [<breakpoint-id-list>]
(gdb) watchpoint delete [<options>] [<breakpoint-id-list>]
```
で指定したブレークポイント、ウォッチポイントを削除
`options`:
- `-d`: 現在無効なリストで指定した以外の全てを削除
- `-f`: 警告なしで全て削除
]
== プログラムの再開
=== 継続実行
#slide(title: "継続実行")[
次の停止場所まで実行する
```shell
(gdb) thread continue [<thread-index>]
```
で継続実行
]
=== ステップ実行
#slide(title: "ステップ実行")[
次の停止箇所を指定しつつ再開
```shell
(gdb) thread step-in
(gdb) thread step-over
```
で次の行まで実行。
補足:
- `step-in`は関数呼び出しの場合中に入る
- `step-over`は関数呼び出しの場合中に入らない
`options`:
- `-c <count>`: ステップ回数
]
== スタックの調査
=== バックトレース
#slide(title: "バックトレース")[
関数呼び出しのトレース
```shell
(gdb) thread backtrace <options>
```
でバックトレースを表示
`options`:
- `-c <count>`: 表示するフレーム数
- `-s <index>`: 表示を開始するフレーム
]
=== フレームの選択
#slide(title: "フレームの選択")[
```shell
(gdb) frame select [<options>] [<frame-index>]
```
でフレームを選択
`options`:
- `-r <offset>`: 現在のフレームからのオフセットで指定
]
=== フレーム関連のステップ実行
#slide(title: "ステップ実行")[
```shell
(gdb) thread step-out
```
で選択中のフレームが返るまで実行
]
== ソースコードの調査
=== リスト
#slide(title: "ソースコード情報の表示")[
```shell
(gdb) source list <options>
```
でソースコードを表示
`options`:
- `-l <linenum>`: 指定した行番号付近を表示
- `-f <filename>`: 指定したファイルを表示
- `-n <symbol>`: 指定した関数を表示
]
== データの調査
=== プリント
#slide(title: "プリント")[
```shell
(gdb) frame variable [<options>] [<varname>...]
```
で選択中のフレームの局所変数の値を表示
`options`:
- `-g`: グローバル変数も表示
- `-l`: 局所変数を非表示
=== 人工配列
- `-Z <len>`: 配列として表示
]
=== レジスタ
#slide(title: "レジスタ")[
```shell
(gdb) register read [<options>] [<register-name>]
```
でベクタ、フロート以外のレジスタを全て表示
`options`:
- `-a`: ベクタ、フロート含む全てのレジスタを表示
]
== 演習2
#slide(title: "演習2")[
#align(center+horizon)[演習2を解いてください。]
]
= プロファイラ
== プロファイラとは
#slide(title: "プロファイラとは")[
- プロファイラ
- プログラムの動作を記録し、動作の統計情報を調べるツール
- 使いどころ
- 作成したプログラムの性能評価
- ホットスポットの調査
- ハードウェア性能情報の監視
== Perf
- Perf
- Linux向けのプロファイラ
]
== コマンド
#slide(title: "コマンド")[
```shell
# perf <command>
```
の形式でコマンドを実行
```shell
# perf
```
で`command`の一覧を閲覧
```shell
# perf help <command>
```
で各コマンドの使い方を表示
```shell
# perf list
```
でイベント(観測できる統計情報)の一覧を表示
]
== stat
#slide(title: "stat")[
```shell
# perf stat [<options>] [<command>]
```
で`command`を実行して統計情報を表示
よく使う`options`:
- `-B, --big-num` : 大きな数字を見やすく表示
- `-e, --event <e>` : 集計するイベントを指定
- カンマで区切って複数指定可
]
== record
#slide(title: "record")[
```shell
# perf record [<options>] [<command>]
```
で`command`を実行してプロファイル情報を収集
よく使う`options`:
- `-e <events>` : 収集するイベントを指定
- `-o <filename>` : 出力ファイル名を指定
- `-g` : コールグラフを有効化
]
== report
#slide(title: "report")[
```shell
# perf report [<options>]
```
で`record`で生成したプロファイル結果を調査
よく使う`options`:
- `-i` : 調査するファイルを指定
- `--stdio` : TUIモードを使用しない
]
== (top)
== 演習3
#slide(title: "演習3")[
#align(center+horizon)[演習3を解いてください。]
]
// #set text(size: 12pt)
// #set page(paper: "a4")
// #block(inset: 30pt)[#outline(indent: 1em)]
|
|
https://github.com/jamesrswift/journal-ensemble | https://raw.githubusercontent.com/jamesrswift/journal-ensemble/main/src/ensemble.typ | typst | The Unlicense | #let color-accent-1 = state("color-accent-1", rgb(174,154,73))
#let color-accent-2 = state("color-accent-2", rgb(42,59,71))
#let rule(
accent-1: rgb(174,154,73),
accent-2: rgb(42,59,71),
) = (body) => {
set page(paper: "a4", numbering: "1")
set text(font: "Open Sans")
set par(leading: 0.75em)
show figure.caption: set align(left)
set figure(gap: 1.2em)
set place(clearance: 2.5em)
color-accent-1.update(accent-1)
color-accent-2.update(accent-2)
body
} |
https://github.com/myst-templates/scipy | https://raw.githubusercontent.com/myst-templates/scipy/main/README.md | markdown | MIT License | # SciPy Proceedings
A typst template for SciPy Proceedings 2024 using MyST Markdown.

|
https://github.com/Dav1com/minerva-report-fcfm | https://raw.githubusercontent.com/Dav1com/minerva-report-fcfm/master/meta.typ | typst | MIT No Attribution | /** meta.typ
*
* Archivo para constantes y estilos usados en documentación,
* y otros elementos sobre el package en sí mismo.
*/
#import "@preview/tidy:0.3.0" as tidy
#let minerva() = {
import "minerva-report-fcfm.typ" as minerva
return minerva
}
#let package-name = "minerva-report-fcfm"
#let package-version = "0.3.0"
#let package-version-arr = (0,3,0)
#let global-namespace = (
"minerva": read.with("minerva-report-fcfm.typ"),
"minerva.departamentos": read.with("lib/departamentos.typ"),
"departamentos": read.with("lib/departamentos.typ"),
"minerva.footer": read.with("lib/footer.typ"),
"footer": read.with("lib/footer.typ"),
"minerva.front": read.with("lib/front.typ"),
"front": read.with("lib/front.typ"),
"minerva.header": read.with("lib/header.typ"),
"header": read.with("lib/header.typ"),
"minerva.rules": read.with("lib/rules.typ"),
"rules": read.with("lib/rules.typ"),
"minerva.states": read.with("lib/states.typ"),
"states": read.with("lib/states.typ"),
"minerva.util": read.with("lib/util.typ"),
"util": read.with("lib/util.typ"),
)
#let global-scope() = ("minerva": minerva())
#let local-namespace(local-file) = {
let local = global-namespace
local.insert(".", read.with(local-file))
return local
}
#let tidy-styles() = { // workaround to inject "minerva" to the example scope
import tidy.styles: default, help
let mine = dictionary(default)
mine.insert("show-example", (..args) => {
let outer-scope = args.named().at("scope", default: (:))
return help.show-example(..args, scope: outer-scope + global-scope())
})
return mine
}
#let help-show(doc) = {
show heading: it => {
show "Parameters": "Argumentos"
show "Example": "Ejemplo"
it
}
show regex("^Default"): "Por defecto"
doc
}
#let help-leaf(module-name) = {
let file-name = "lib/" + module-name + ".typ"
let base-func = tidy.generate-help(
namespace: local-namespace(file-name),
package-name: package-name + module-name,
style: tidy-styles()
)
return (..args) => {
show: help-show
base-func(..args)
}
}
|
https://github.com/kokkonisd/yahtzee-scoreboard | https://raw.githubusercontent.com/kokkonisd/yahtzee-scoreboard/main/scoreboard.typ | typst | #let MAIN_FONT = "FreeSerif"
#let HEADER_TEXT_SIZE = 30pt
#let NORMAL_TEXT_SIZE = 18pt
#let SMALL_TEXT_SIZE = 12pt
#set page(margin: 10pt)
#show text: it => { smallcaps(it) }
#set text(size: NORMAL_TEXT_SIZE, font: MAIN_FONT)
#v(2cm)
#block(width: 100%)[
#set align(center + horizon)
#stack(
dir: ltr,
spacing: 4pt,
box[#line(length: 3cm)],
box[#text(size: HEADER_TEXT_SIZE)[
#show par: set block(spacing: 0pt)
*_Yahtzee!_*
⚀ ⚁ ⚂ ⚃ ⚄
]],
box[#line(length: 3cm)],
)
]
#set align(center + horizon)
#block[
#table(
columns: (auto, 2pt, 1fr),
rows: (
auto,
2pt,
auto,
auto,
auto,
auto,
auto,
auto,
auto,
2pt,
auto,
auto,
auto,
auto,
auto,
auto,
auto,
auto,
2pt,
auto
),
inset: 10pt,
align: left + horizon,
[*Player*], [], [],
[], [], [],
[*1s*], [], [],
[*2s*], [], [],
[*3s*], [], [],
[*4s*], [], [],
[*5s*], [], [],
[*6s*], [], [],
[
*Bonus _+35_ \
#text(size: SMALL_TEXT_SIZE)[(if sum > 63)]*
], [], [],
[], [], [],
[*Sum*], [], [],
[*3 of a Kind*], [], [],
[*4 of a Kind*], [], [],
[*Full House (_25_)*], [], [],
[*Small Straight (_30_)*], [], [],
[*Large Straight (_40_)*], [], [],
[*Yahtzee! (_50_)*], [], [],
[
*Bonus Yahtzee! _+50_ \
#text(size: SMALL_TEXT_SIZE)[(if Yahtzee!)]*
], [], [],
[], [], [],
[*Total*], [], [],
)
]
|
|
https://github.com/rabotaem-incorporated/algebra-conspect-1course | https://raw.githubusercontent.com/rabotaem-incorporated/algebra-conspect-1course/master/sections/01-number-theory/01-divisibility.typ | typst | Other | #import "../../utils/core.typ": *
== Делимость
#def[
$a, b in ZZ, a | b <==> exists c in ZZ: b = a c$
]
#prop[
+ $a divides a$ --- рефлексивность
+ $a divides b, b divides c ==> exists c in ZZ: b = a c$ --- транзитивность
+ $a divides b, k in ZZ ==> k a divides k b$
+ $a divides b_1, a divides b_2 ==> a divides (b_1 plus.minus b_2)$
+ $plus.minus 1 divides a$
+ $cases(
k a space.hair divides space.hair k b,
k eq.not 0
) ==> a divides b$
]
#def[
$a, b$ называются _ассоциированными_, если $a divides b$ и $b divides a$.
Иногда такое отношение обозначают $a sim b$:
$ a sim b <==> a divides b and b divides a $
]
#prop[
+ Пусть $a sim a'$, $ b sim b'$. Тогда $a divides b <==> a' divides b'$.
] |
https://github.com/liuzhuan/reading-list | https://raw.githubusercontent.com/liuzhuan/reading-list/master/books/programming-with-types/note.typ | typst | #import "../../templates/notes.typ": notes
#show: rest => notes(rest)
= 类型简介
== 为什么存在类型
=== 0 和 1
=== 类型和类型系统的定义
== 类型系统的优点
=== 正确性
=== 不可变性
=== 封装
=== 可组合性
=== 可读性
== 类型系统的类型
=== 动态类型和静态类型
=== 弱类型和强类型
=== 类型推断
= 基本类型
== 设计不返回值的函数
=== 空类型
=== 单元类型
== 布尔逻辑和短路
== 数值类型的常见陷阱
== 编码文本
== 使用数组和引用构建数据结构
= 组合
= 类型安全
= 函数类型
= 函数类型的高级应用
= 子类型
|
|
https://github.com/Kasci/LiturgicalBooks | https://raw.githubusercontent.com/Kasci/LiturgicalBooks/master/CSL_old/oktoich/Hlas5/6_Sobota.typ | typst | #let V = (
"HV": (
("","Rádujsja póstnikom","Plámeň nečéstija ľútaho strastotérpcy uhasíša krovéj svojích tečéňmi, blahočéstija svítlosť v míri vsém vozžéhše múčenicy, bóhi že lžeimenítyja, i ťích zlovónija, i chrámy do koncá popalíša: svít vozsijáša súščym na zemlí čisťijšij, ímže i prosviščájemi, ťmý izbihájem bezbóžija, i prélesti ídoľskija ukloňájemsja, Christú poklaňájuščesja, podajúščemu mírovi véliju mílosť."),
("","","Slovesá jeretík zločestívych, i lovlénija udób razrušívše, orúžnicy Otcá beznačáľnaho, Sýna sobeznačáľnaho, i svjatáho Dúcha býste, v trijéch lícich jedínstvu Božestvá, blahočestnomúdrenňi vírnych naučájušče i utverždájušče pravoslávnuju própoviď. Ťímže i blažími jesté, pástyrije vsesvjaščénniji: jáko na pážitech živonósnych Christóvo stádo upasóste, za nehóže vsjá boľízni i napásti mnohoobráznyja preterpíste."),
("","","Strásti plotskíja udób do koncá poprá, podvíhšejesja prepodóbnych soslóvije, vlastelína umá ďijánijem dobroďítelej prijémše: ímže bisóvskija vsjá kózni pobidíša dóblestvenňi, i ánhelom sobesídnicy javíšasja, jáko bezplótniji požívše. Ímže i nýňi srádujutsja v výšnich obítelech, svítlo živúšče, i Christú predstoját, ot nehó prosjášče dušám nášym darováti véliju mílosť."),
("","","Ščitóm víry obólkšesja, i známenijem krestnym sebé ukrípľše, k múkam múžeski vdášasja, i dijávoľu hordýňu i lésť uprazdníša svjatíji tvojí, Hóspodi, ťích molítvami jáko vsesíľnyj Bóh, míru mír nizposlí, i dušám nášym véliju mílosť."),
("","","Ščitóm víry obólkšesja, i známenijem krestnym sebé ukrípľše, k múkam múžeski vdášasja, i dijávoľu hordýňu i lésť uprazdníša svjatíji tvojí, Hóspodi, ťích molítvami jáko vsesíľnyj Bóh, míru mír nizposlí, i dušám nášym véliju mílosť."),
("","","O zemných vsích nebréhše, i na múki múžeski derznúvše, blažénnych nadéžd ne pohrišíste, no nebésnomu cárstviju nasľídnicy býste, prechváľniji múčenicy: imúšče derznovénije k čelovikoľúbcu Bóhu, míru mír prosíte, i dušám nášym véliju mílosť."),
("Bohoródičen","","V čermňím móri, neiskusobráčnyja nevísty óbraz napisásja inohdá. Támo Moiséj, razďilíteľ vodý zdé že Havrijíl, služíteľ čudesé. Tohdá hlubinú šéstvova nemókrenno Izráiľ: nýňi že Christá rodí bezsímenno Ďíva. Móre po prošéstviji Izráilevi prebýsť neprochódno: neporóčnaja po roždeství Jemmanúilevi prebýsť netľínna. Sýj, i préžde sýj, javléjsja jáko čelovík, Bóže pomíluj nás."),
),
"S": (
("","","Molíte za ný svjatíji múčenicy, da izbávimsja ot bezzakónij nášich: vám bo daná býsť bláhodáť molítisja o nás."),
("","","Nesýtnoju ľubóviju duší, Christá ne otverhóstesja svjatíji múčenicy: ľútyja i razlíčnyja rány strastéj preterpíste, mučítelej hordýňu nizložíste: nepreklónnu i nevredímu víru sochráňše, na nebesá prestávistesja. Ťímže i derznovénije imúšče k nemú, prosíte darováti nám véliju mílosť."),
("Mértven","","Pomjanúch proróka vopijúšča: áz jésm zemľá i pépeľ, i páki razsmotrích vo hrobích, i víďich kósti obnažénnyja, i rích úbo: któ jésť cár, ilí vóin, ilí bohát, ilí níšč, ilí právednik, ilí hríšnik? No upokój Hóspodi s právednymi rabý tvojá, jáko čelovikoľúbec."),
("Bohoródičen","","Obrádovannaja, chodátajstvuj tvojími molítvami, i isprosí dušám nášym mnóžestvo ščedrót, i očiščénije mnóhich prehrišénij mólimsja."),
),
)
#let P = (
"1": (
("","","Koňá i vsádnika v móre čermnóje, sokrušájaj bráni, mýšceju vysókoju, Christós istrjasé: Izráiľa že spásé, pobídnuju písň pojúšča."),
("","","Vsí ťa čelovíčestiji ródi chváľat, jáko drévle Ďívo, proróčeski proreklá jesí: i mené úbo prijimí pojúšča ťá Vladýčice, i prosvití, i vrazumí."),
("","","Pritupíla jesí smérti žálo, i mirskíj hrích Ďívo, ístinnuju róždši žízň, jejáže rádi Vladýčice, pritupí strastéj mojích óstryja stríly vskóri."),
("","","Jedína ispeščréna ďivíčeskimi rjásnami ot víka jávľšisja, smokóvnuju rízu Adámovu tý rastórhnula jesí: ťímže mjá nýňi oblecý cilomúdrija odéždeju molítvami tvojími."),
("","","Bohátstvo i božéstvennuju slávu sťažáša úbo mnóhi dščéri préžde jávi, no bez sravnénija Vladýčice, tý vsích prevozšlá jesí. Ťímže mjá nýňi obohatí nebésnymi i božéstvennymi blahodáťmi."),
),
"3": (
("","","Vodruzívyj na ničesómže zémľu poveľínijem tvojím, i povísivyj neoderžímo ťahoťíjuščuju, na nedvížimim Christé, kámeni zápovidej tvojích, cérkov tvojú, utverdí, jedíne bláže i čelovikoľúbče."),
("","","Hlubiná i vysotá v tebí poznavášesja Ďívo prečístaja, Bóžijej múdrosti nepostižímij, ot tvojích ložésn róždšejsja: jéjuže hlubiný sérdce mojé izbávi mudrovánij zmiínych."),
("","","Íže préžde pernátyja, i hády, ot vodý sostávil jesí slóvom, ne súščyja préžde: tý ábije Christé ot króve čístyja Ďívy, božéstvennaho tvojehó voploščénija odéždu stránnu ustróil jesí."),
("","","Tý jedína očiščénije javílasja jesí jestestvú, prečístaja, v ňúže óhň božéstvennyj neopáľno vséľsja, sijé očísti jávi: tý úbo sohrišénij i strastéj mojích skvérnu očísti, i tvojími molítvami prosvití mja."),
("","","Čášu nóvaho vinohráda róždija, napojájuščuju jávi vírnyja vo ostavlénije sohrišénij, ťá prečístaja vídyj, moľú: ispuščénijem božéstvennyja vodý napój sérdce mojé."),
),
"4": (
("","","Božéstvennoje tvojé razumív istoščánije, prozorlívo Avvakúm, Christé, so trépetom vopijáše tebí: vo spasénije ľudéj tvojích, spastí pomázannyja tvojá prišél jesí."),
("","","Neorána tý javílasja jesí brazdá, nesíjannyj božéstvennyj prozjábšaja klás, ímže álčušča mjá nakormí božéstvennymi darováňmi že i blahodáťmi."),
("","","Boľášča mjá ískrenno smértne, i dušévnych strastéj ohném soderžíma Vladýčice, molítv tvojích vodóju napojívši, vskóri vozstávi."),
("","","Jáko súščij Bóžij hrád oduševlén, jehóže ríki mýslennyja veseľát stremlénija, molítv tvojích stolpóm duší mojejá chráminu utverdí."),
("","","Óblak ťá vídyj, odoždívšij právdu ístinnuju, moľú prečístaja Vladýčice, ot vsích obíďaščich mjá izbáviti rabá tvojehó vskóri."),
),
"5": (
("","","Oďijájsja svítom jáko rízoju, k tebí útreňuju, i tebí zovú: dúšu mojú prosvití omračénnuju Christé, jáko jedín blahoutróben."),
("","","Vozmuščénije i vólnu hrichá, i strastéj mojích Ďívo Vladýčice, do koncá utiší, bezstrástija róždši vinóvnaho."),
("","","Postáv sýj svýše Christóv javísja, blahoľípija odéždy božéstvennyja, dobroďítelej odéždeju čístaja, obnažénnuju dúšu mojú oblecý."),
("","","Očiščénije mí dáruj sohrišénij, tvojími moľbámi čístaja Ďívo, jáže očiščénije božéstvennoje róždšaja nám Christá i Hóspoda."),
("","","Strúpy, jázvy i hnojénija hrichóvnaja, rukoďíjstvija, molítvami potrebí mi Ďívo, i sílu rabú tvojemú podážď."),
),
"6": (
("","","Neístovstvujuščejesja búreju dušetľínnoju, Vladýko Christé, strastéj móre ukrotí, i ot tlí vozvedí mjá, jáko blahoutróben."),
("","","Jáže svít róždšaja svitílam tvoríteľnyj, dúšu mojú nýňi prosvití, i izbávi ot strastéj omračénija, vsesvítlaja."),
("","","Mérry usladívšaho vódy préžde Bohoródice, tvojehó Sýna molí, izbáviti mjá strásti ľútyja, i hóresti vskóri."),
("","","Vozmuščájet potók strastéj dúšu mojú, prečístaja: no sehó izsuší molítvami tvojími, i pómysly lukávyja potrebí."),
("","","Christós izbavľája čelovíki priíde ot Sijóna, iz čréva tvojehó Vladýčice preneporóčnaja: ímže i mené ot napástej izbávi i skorbéj."),
),
"S": (
("","","Vskúju unyvájušči dušé strástnaja, zabýla jesí Bóha tvojehó mílujuščaho ťá? I poveľínija jehó preobíďivši, v bluďí žitijé skončaváješi umovrédno: otstupí ot zlóby, Bohoródice vopijúšči: otčájannuju dúšu mojú pomíluj."),
),
"7": (
("","","Prevoznosímyj otcév Hospóď plámeň uhasí, ótroki orosí, sohlásno pojúščyja: Bóže, blahoslovén jesí."),
("","","Užasájutsja i trepéščut tvojehó prizyvánija prečístaja, bisóvstiji polcý: ot níchže izbavľájušči mjá spasí, i sobľudí, pokryvájušči ot vsjákaho vréda."),
("","","Neizhlahólannaja sláva tvojá Ďívo, slávy bo Hóspoda rodilá jesí: ťímže mjá spodóbi slávy Sýna tvojehó i Bóha mojehó, tvojími molítvami."),
("","","Preklonísja k moľbám tvojehó rabá Vladýčice, i izbávi mjá vskóri bíd i skorbéj, i vsjákich iskušénij, vídimych i nevídimych."),
("","","Vsehó mjá strasťmí studá prečístaja, okaľávšasja i oskvernívšasja, čistotóju omýj, i ujasní Ďívo, molítvami tvojích okroplénij."),
),
"8": (
("","","Tebí vseďíteľu v peščí ótrocy, vsemírnyj lík splétše, pojáchu: ďilá vsjákaja Hóspoda pójte, i prevoznosíte vo vsjá víki."),
("","","Vodá neplódstvija strástna, duší mojejá ložesná neplódna sotvorí, i izsuší: odoždí mi léhkij óblače, božéstvennuju rósu, jáko da vozraščú plodý pokajánija."),
("","","Vólnu pomyšlénij strástnych i búrju utiší prečístaja, tvojími molítvami: naprávi že mjá k tečéniju bezstrástija, da ťá slávľu tépľi vo víki vsjá."),
("","","Dvére mýslennaja, i zatvorénaja vratá, ímiže jedín prójde Bóh, dvéri zahradí i zakľučí strastéj mojích, i upovánija otvérzi mí vratá."),
("","","Vozmí ot mené prehrišénij brémja, Máti Ďívo, jáže jedína vzémľuščaho míra vsehó vés hrích, róždšaja neskázanno áhnca Bóžija i Slóva."),
),
"9": (
("","","Isáije likúj, Ďíva imí vo čréve, i rodí Sýna Jemmanúila, Bóha že i čelovíka, vostók ímja jemú: jehóže veličájušče, Ďívu ublažájem."),
("","","Oskvernív jáko čelovík dúšu mojú prehrišéňmi mnóhimi, i strasťmí plotskími okaľávsja, ťá moľú nýňi priľížno, i míl sjá ďíju: očísti mjá čístaja, tvojími molítvami ot vsjákija zlóby."),
("","","Volíteľa mílosti rodilá jesí, ščedrót čelovikoľúbca Bóha, jedínaho blaháho, dolhoterpilívaho i blahoutróbnaho: jehóže blahopremínna pokaží mi čístaja, tvojími moľbámi, i sohrišénij razrišénije podážď."),
("","","Dremánijem oderžíma unýnija, i slasťmí spjášča mjá nýňi, Vladýčice, rabá tvojehó vozdvíhni k dobroďítelem ďijánij blahích, neusýpnymi tvojími máternimi molítvami."),
("","","Blahoslovjá blahoslovľú ťa prečístaja, i veličáju tépľi: blahosloví mja úbo tvojehó pivcá, i vsjáčeskich núždnych i pečáľnych izbávi, i sochraní tvojíma dláňma nepobidíma."),
),
)
#let U = (
"S1": (
("","","Sijájet dnés pámjať strástotérpec, ímať bo i ot nebés zarjú: lík ánheľskij toržestvújet, i ród čelovíčeskij sprázdnujet. Ťímže móľatsja Hóspodevi, pomílovatisja dušám nášym."),
("","","Čudesá svjatých tvojích múčenik sťínu nerazorímu nám darovál jesí, Christé Bóže: ťích molítvami vírnyja ľúdi tvojá utverdí, jáko jedín bláh i čelovikoľúbec."),
("Bohoródičen","","Rádujsja, dvére Hospódňa neprochodímaja, rádujsja, sťinó i pokróve pritekájuščich k tebí, rádujsja, neoburevájemoje pristánišče, i neiskusobráčnaja, róždšaja plótiju tvorcá tvojehó i Bóha: moľášči ne oskuďiváj o vospivájuščich, i kláňajuščichsja roždestvú tvojemú."),
),
"S2": (
("","","Hóspodi, čáši strastéj tvojích strastotérpcy tvojí porevnovávše, ostáviša žitéjskuju krasotú, i býša ánhelom sopričástnicy: ťích moľbámi podážď dušám nášym mír Christé Bóže, i véliju mílosť."),
("","","Svjatých múčenik ispravlénijem nebésnyja síly preudivíšasja, káko v ťíľi mértvenňim podvíhšesja dóbri, bezplótnaho vrahá síloju krestnoju pobidíša nevídimo: i móľatsja Hóspodevi, pomílovatisja dušám nášym."),
("Pokóin","","Pokój Spáse náš s právednymi rabý tvojá, i ťích vselí vo dvorý tvojá, jákože písano jésť, prezirája vsjá sohrišénija ích, jáko bláh, vólnaja i nevóľnaja, i vsjá jáže v víďiniji i ne v víďiniji, čelovikoľúbče."),
("Bohoródičen","","Ot Ďívy vozsijávyj míru Christé Bóže, sýny svíta tóju pokazávyj, pomíluj nás."),
),
"K": (
"P1": (
"1": (
("","","Zémľu, na ňúže ne vozsijá, ni víďi sólnce kohdá: bézdnu, júže ne víďi náhu širotá nebésnaja, Izrájiľ prójde nevlážno Hóspodi, i vvél jesí jehó v hóru svjatýni tvojejá, chváľašča i pojúšča pobídnuju písň."),
("","","Ťilesá predajúšče nekrótkim sudijám, preterpíste nesterpímyja rány dóbliji stradáľcy, čájušče prijáti póčesti svýše: i vvedé vás Christós vo víčnyja obíteli, rádujuščichsja i pojúščich pobídnuju písň,"),
("","","svjatítelem: Prepodóbniji i právedniji, i svjatítelije, blahoslávniji soveršívše poveľínija Bóžija, upasóša ľúdi, i dóbri nastáviša k voďí rázuma: i potóki sládosti dostójno vosprijáša, istočájušče blahodátiju iscilénij ríki."),
("","","Naprávi mjá Hóspodi, k pristániščem životá, molítvami prorók preslávnych, premúdrych pervosvjatítelej, i svjaščénnych žén postradávšich krípko, i postóm vrahá poprávšich, múžeskim umóm, božéstvennoju tebé blahodátiju jávľšahosja na zemlí."),
("Pokóin","","Tebé mólim blahopremínnaho Bóha: upokój v ňídrich avraámovych rabý tvojá Christé, jáže k tebí prestávil jesí ot žitéjskaho mjatéža, i spodóbi ích svíta víčnaho, ťích sohrišénija prezirája jáko bláh."),
("","","Rádujsja, tebí zovém, róždšej rádosť vsepítaja: prosvití náša umý i dúšy, i k stezjám rázuma vsích naprávi, i prehrišénij vsím očiščénije dáti molí jedína Bohonevísto, Sýna tvojehó i Bóha."),
),
"2": (
("","","Spasíteľu Bóhu, v móri ľúdi nemókrymi nohámi nastávľšemu, i faraóna so vsevóinstvom potópľšemu, tomú jedínomu poím, jáko proslávisja."),
("","","Božéstvennoju ľubóviju strastotérpcy Christóvy mučítelej hordýňu popráša: prestávlennym že víroju mílostivnoje prósjat ostavlénije i pokój."),
("","","Vo svjatých selénijich, vo dvórich tvojích Christé, prestávlennyja vselí! Íže dólh za ních prolijávyj króv tvojú Vladýko, prečestňíjšuju."),
("","","Premúdrosť Bóžija, íže izvístno načertánije vsé nosjáj Rodítelevo: íchže priját ščédre, sám upokój, podavája ím prisnosúščnoje blažénstvo."),
("","","Svitonósnaja síň, zlatovídnyj kovčéh, božéstvennoje Slóvo obderžášči voploščénnoje nás rádi, i razorívšeje smértnuju sílu, javílasja jesí vseneporóčnaja."),
),
),
"P3": (
"1": (
("","","Dvížimoje sérdce mojé Hóspodi, volnámi žitéjskimi, utverdí, v pristánišče tíchoje nastavľája jáko Bóh."),
("","","Pálicami bijémo ne poščaďíste ťílo, i mečí sikómo vsechváľniji orúžnicy, ukripľájemi nadéždeju múčenicy víčnych krasót."),
("","","Svjatíteľstva odéždu prosvitíste, vídy dobroďítelnymi upásše Christóvo stádo na pážitech živótnych."),
("","","Plóť umerščvľájušče vozderžánijem prepodóbniji, žízni božéstvenňij pričastíšasja: ťích Christé svjaščénnymi molítvami ot bíd izbávi nás."),
("","","Usópšym támošnij pokój čelovikoľúbče podážď, jáže soďíjaša na zemlí, dólhi otpuščája jáko bláh."),
("","","Blahoslovénnuju v ženách ťá jáko víďi, soslóvije žénskoje postradá, i tvojemú Sýnu, Ďívo Máti, privedésja."),
),
"2": (
("","","Utverdí ný Bóže Spáse, tvojéju síloju, i vozdvíhni róh tvojejá cérkve, pravovírno chváľaščich ťá."),
("","","Múžeski podvíhšesja stradáľcy, mučíteľskim stremlénijem protívu stáša, i móľatsja o usópšich Christú."),
("","","Zakóny tvojími vospitávšichsja, prestávľšichsja preblahíj, v svítlych tvojích selénijich prijém, upokój."),
("","","Mílostivyj jedíne Bóže, jáže izbrál jesí, spodóbi svjatých svítlostej, prezirája ťích sohrišénija."),
("","","Pojém tvojé roždestvó čístaja, ímže pérvaho osuždénija i kľátvy izbávichomsja, i ot smérti svobodíchomsja."),
),
),
"P4": (
"1": (
("","","Uslýšach Hóspodi slúch tvój, i ubojáchsja, razumích smotrénije tvojé, i proslávich ťá jedíne čelovikoľúbče."),
("","","Síloju tvojéju Hóspodi, strastotérpcy vrážiju sílu popráša, i kríposť býša vírnym, i velíkoje utverždénije."),
("","","Prepodóbniji vsí rádostiju rádujutsja, i oďivájutsja svjaščénnicy božéstvenniji v právdu, jákože v rízu."),
("","","Vospojím vsí Bohohlahólivyja Bóžija proróki, i počtím žén soslóvije, jáže dóbri tečénije skončávšyja."),
("","","K pristánišču tvojehó cárstvija Vladýko, ustremív, upokój, íchže prestávil jesí ot mjatéža i búri nastojáščaho žitijá."),
("","","Bezľítnyj býsť nýňi pod ľítom iz tebé Ďívo: tohó molí razrušíti vsjá duší mojejá ľítnaja prehrišénija."),
),
"2": (
("","","Uslýšach Hóspodi, iz hróba tvojé vostánije, i proslávich tvojú nepobidímuju sílu."),
("","","Soprisnosúščna ťá Otcú ispovídavše blahočéstno múčenicy Christé, ubijéni býša, i vopijút tí: izbávi íchže prijál jesí rabý tvojá."),
("","","Íže v mertvecích bývyj jedín svobóď mertvéc Christé, i mertvecém žízň víčnuju dáruja, pokój dážď nýňi prestávlenym rabóm tvojím."),
("","","Prišédyj vo jéže spastí zablúždšyja Christé, rájskaho spodóbi vselénija, jáže prestávil jesí vo víri, opravdávyj blahodátiju."),
("","","Osiní ťa výšňaho otrokovíce síla, v tebí ráj soďíla živótnyj, drévo imúščij posreďí, chodátaja i Hóspoda."),
),
),
"P5": (
"1": (
("","","Okajánnuju dúšu mojú, noščeborjúščujusja so ťmóju strastéj, predvarív uščédri, i vozsijáj mýslennoje sólnce dnesvítlyja zvizdý vo mňí, vo jéže razďilíti nóšč ot svíta."),
("","","Iscilénije nedúhujuščym istočájut kósti múčenik: ne sokrušívšesja bo zlóboju, i náša obnovľájut sokrušénija: vsjá že kósti zločéstija jáko prách istníša."),
("","","Zakóny tvojá sobľudájušče svjatítelije upasóša ľúdi, i nastáviša ščédre, k životú búduščemu: prepodóbniji že umertvíša strastéj mučíteľstvo soveršénnym umóm."),
("","","Da počtútsja prorócy, i s ními vsí právednicy víroju, i da pochváľatsja prepodóbno požívšiji, i múkami prosvitívšijisja na zemlí božéstvennyja žený, jáko rabý Christóvy."),
("Pokóin","","Jáže ot zemlí priját, v nebésnych učiní selénijich vírnyja rabý tvojá, ťích prezirája prehrišénija, za premnóhuju bláhosť Christé, voploščéjsja nás rádi zemných."),
("Bohoródičen","","Pojém ťá Ďívo, jejáže rádi javísja Bóh súščym na zemlí, čelovík býv, vopijúšče: rádujsja, zemlé blahoplodovítaja, plodonosjáščaja klás tájny, pitájušč vsjákoje dychánije."),
),
"2": (
("","","Útreňujušče vopijém tí Hóspodi, spasí ný, tý bo jesí Bóh náš, rázvi bo tebé inóho ne znájem."),
("","","Múčenik prijém Hóspodi, molénija, dúšy, jáže prestávil jesí, so izbránnymi tí pričtí."),
("","","Predrékl jesí, ne uzríti smérti vírujuščym v ťá: ťímže Vladýko usópšyja upokój."),
("","","Krasotý dómu tvojehó Hóspodi, tvojá rabý ulučíti spodóbi, i sládkaho pričástija."),
("","","Slóvo, jéže Otcú soprisnosúščnoje, ot Ďívy voplóščsja, umertví smértiju smérť."),
),
),
"P6": (
"1": (
("","","Jákože proróka ot zvírja izbávil jesí Hóspodi, i mené iz hlubiný nesoderžímych strastéj vozvedí, moľúsja: da priložú prizríti mí k chrámu svjatómu tvojemú."),
("","","Ťilesá predávše na rány božéstvenniji múčenicy, mučítelej rukám, veseľáchusja dušéju: božéstvennoje bo zrjáchu voístinnu, prisnosúščnoje rádovanije i božéstvennaja vozdajánija."),
("","","Sláva premúdrym svjatítelem i prepodóbnym tý jesí Christé: molítvami ích tvojá ľúdi uščédri, íchže svojéju króviju sťažál jesí, jáko čelovikoľúbec."),
("","","Ot tebé Hóspodi, prosviščájuščesja umóm prorócy, projavľájut jásno dálňaja jákože blíz: žený že síloju tvojéju deržávu vrážiju razrušíša, stradánijem i postóm."),
("","","Prestávlenyja ot nás vírnyja rabý tvojá, likóm izbránnych sopričtáv bláže, upokój Hóspodi, vsjá ťích sohrišénija prezirája za milosérdije."),
("Bohoródičen","","Sozdávyj v načátci Jévu Hóspodi, Ďívy v ložesná všéd, náše soďílovaješi obnovlénije v rábij óbraz obólksja, íže Vladýka vsjáčeskich."),
),
"2": (
("","","Obýde mjá bézdna, hrób mňí kít býsť: áz že vozopích k tebí čelovikoľúbcu, i spasé mja desníca tvojá Hóspodi."),
("","","Vóinstvo múčenik tvojích, výšnim sílam podóbjaščesja, Christé, móľat ťá, podážď čelovikoľúbče, prestávlenym jéže ot tebé naslaždénije."),
("","","V mísťich prochlaždénija, v mísťich svjatých svítlosti, v mísťich oslablénija Christé, jáko čelovikoľúbec, íchže prijál jesí, učiní rabý tvojá."),
("","","Očísti rabý tvojá, i ťím sohrišénij proščénije podážď čelovikoľúbče, i žízni spodóbi netľínňij, i blažénnomu nasľídiju."),
("Bohoródičen","","Začátija bezsímennaho tvojehó, któ slóvom izreščí móžet čudesé, vseneporóčnaja: Bóha vo rodilá jesí, za milosérdije k nám prišédša."),
),
),
"P7": (
"1": (
("","","Ohňá hasílišče otrokóv molítva, orošájuščaja péšč, propovídnica čudesé, ne opaľájušči, nižé sožihájušči pisnoslóvcy Bóha otéc nášich."),
("","","Vý razžizájemi ľútych mučénij ohném, ľublénije tepľíjšeje múčenicy slávniji pokazáste ko Hóspodu, prochlaždájušče vás pómyslom blahočestívym."),
("","","Premúdrostiju Dúcha ukrasívšesja premúdriji, i svítlo požíste, svjaščennoďíjstvujušče blahodáti Jevánhelia, i jáko Bóžija služíteli pochvaľájem vás."),
("","","Vý umertvívše plóť boľízňmi mnóhimi, žízni spodóbistesja búduščija prepodóbniji, moľáščesja sijú polučíti nám umerščvlénym strastéj priložéňmi."),
("","","Blažénnyj lík Bóžijich prorók, i žén sobór, podvíhšyjasja postóm, i stradánijem nizložívšyja vrahá, da pochváľatsja vírno."),
("","","Mértvym priobščívsja vsích žízň Slóve, nýňi ostávľšich žitijá mjatéž, ko pristánišču tvojemú božéstvennomu uprávi, sohrišénija ích prezirája bláže."),
("","","Íže Bohoródicu ťá múdrstvujuščiji rázumom právym, ohňá víčnaho i ťmý da izbávimsja chodátajstvom tvojím Vladýčice, i nevídimych vráh borjúščich nás."),
),
"2": (
("","","V peščí óhnenňij pisnoslóvcy spasýj ótroki, blahoslovén Bóh otéc nášich."),
("","","Nýňi nepristúpnaho svíta nasýtitisja, podážď Spáse, prestávlenym, moľbámi strastotérpec tvojích."),
("","","V cérkvi pérvenec Christé, vo víri skončávšichsja, ščédre, sopričtí."),
("","","Ukrášeny odéždami netľínija tvojá rabý, prestávlenyja k tebí Spáse, upokój."),
("","","Tók smértnaho suščestvá otsiklá jesí prečístaja, žízň bez símene začénši, vseneporóčnaja."),
),
),
"P8": (
"1": (
("","","Ánhelov sónm, čelovíkov sobór, carjá i ziždíteľa vsích, svjaščénnicy pójte, blahoslovíte levíti, ľúdije prevoznosíte vo vsjá víki."),
("","","Preplývše mučénij pučínu okormlénijem slóva, stradáľcy krovéj tečénijem pohruzíste vsjá polkí ľstívaho, i živeté vo víki."),
("","","Premúdriji bývše svjaščennoďílatelije, svjaščénno na voďí pravoslávija vám vvírennoje stádo prepitáste: voístinnu sládosti krásnych potókov naslaždájetesja vo víki."),
("","","Svitíla prepodóbniji vírnym javístesja, jáko soveršívše ďilá svíta, i k božéstvenňij svítlosti prestávistesja: ťmý nás svobodíti molítesja Vladýci."),
("","","Veselísja soslóvije žénskoje, póčestej ispolnénije vsjákich prijémšeje ránami, i lík rádujsja proróčeskij, i právednych, uhodívšich Christú vo víki."),
("Bohoródičen","","Orúžije obraščájuščejesja nýňi, dážď Vladýko nevozbránno proití, prestávlenym ot žitijá rabóm tvojím: vnútr rajá ťích vseľája, jáko jedín mílostiv."),
),
"2": (
("","","Jáko vratá vvoďáščaja k božéstvennomu vchódu, jáko dobrovoschódnuju ľístvicu Bóžiju, jáko spasájuščymsja nezablúdnuju nastávnicu, obrádovannuju vospojím Ďívu Maríju."),
("","","Iz Otcá préžde vík roždénnaho Sýna i Bóha, i v posľídňaja ľíta voploščénnaho ot Ďívy Mátere, svjaščénnicy pójte, ľúdije prevoznosíte vo vsjá víki."),
("","","Íže svjatých múčenik pódvihi prijémyj, i ťích rádi upokojájaj vo víri tvojéj usópšyja, tebé Spáse pojém, i prevoznósim vo vsjá víki."),
("","","Premírnyja tvojejá slávy sijánijem ozarjátisja, jáže ot nás prestávlenyja spodóbi, jáko blahoutróben, tebé Spáse pojúščyja, i prevoznosjáščyja vo vsjá víki."),
("","","S líki svjatých, íchže prestávil jesí, učiní, i Avraámu, v ňídrich s Lázarem pričtí tebé Spáse pojúščich, i prevoznosjáščich vo vsjá víki."),
("Bohoródičen","","Ukrášena dobrótoju čistotý, Ďívo Máti, dobrotvórnaho blahoľípija žilíšče bývši: ťímže ťá pojém, i prevoznósim čístuju vo vsjá víki."),
),
),
"P9": (
"1": (
("","","Jáko sotvorí tebí velíčija sílnyj, Ďívu jávľ ťá čístu po roždeství, jáko róždšuju bez símene svojehó tvorcá: ťím ťá Bohoródicu veličájem."),
("","","Svjáščennoďíjstvenniji pástyrije prorók svjatých lík, právednych neizčétnoje mnóžestvo: múčenikov sobór, svjaščénnymi písňmi da ublažájutsja: moľáščesja spastísja dušám nášym."),
("","","Jáko čúdnyj póstničestvovav prepodóbnych sobór premúdrenno, čudés pokazáňmi mnóhimi nýňi udivísja: ťích moľbámi dívnyj Hóspodi, udiví na vsích mílosti tvojá."),
("","","So svjaščennomúčeniki skončávšimi tečénije dóbri, žén bezčíslennoje mnóžestvo postradávšeje i postívšejesja, ľubóviju da ublažájetsja vírno, so ánheľskimi líki prebyvájuščeje."),
("","","Svjatých vsích mnóžestvo mólit ťá Slóve: upokój mnóžestva jáže vo víri ot zemlí prestávlenyja, za mnóžestvo mílosti, jáže soďíjanaja ími v žitií, prezirája sohrišénija."),
("Bohoródičen","","Umovrédno hrichí soďíjach mnóhi Ďívo, mučénija ožidáju próčeje, ot nehóže mjá izbávi, nesumňínnym sérdcem k tebí prichoďáščaho, i božéstvennyj pokróv tvój prizyvájušča."),
),
"2": (
("","","Ťá páče umá i slovesé Máter Bóžiju, v ľíto bezľítnaho neizrečénno róždšuju, vírniji jedinomúdrenno veličájem."),
("","","Stradánij svjaščénnych múčenicy, vozdajánija prijémše, darováti ťá nýňi móľat, víroju prestávlenym Spáse, oslablénije."),
("","","Umerščvlénije preterpíl jesí jedíne Spáse bezsmértne, íže voskresénije mértvym podajá jáko blahoutróben, i bezsmértija svítlosť."),
("","","Isprávil jesí nás pádšich v smérť, i na živót víčnyj naďíjatisja naučíl jesí, jehóže ulučíti tvojím rabóm Spáse, dáruj."),
("Bohoródičen","","Zakóna síni preidóša roždestvóm tvojím, ístina vozsijá, blahodáť darovásja Bohoródice: ťímže ťá veličájem."),
),
),
),
"CH": (
("","","Blahoslovéno vóinstvo nebésnaho Carjá: ášče bo i zemnoródni bíša strastotérpcy, no ánheľskij sán tščáchusja dostíhnuti, o ťilesích neradívše, i strastéj rádi bezplótnych spodóbišasja čésti. Ťímže molítvami ích Hóspodi, spasí dúšy náša."),
("","","Strastonóscy tvojí Hóspodi, činóm ánheľskim upodóbľšesja, jáko bezplótniji, múki preterpíša, i jedinomýslenno upovánije imúšče, obiščánnych bláh naslaždénije. Molítvami ích Christé Bóže, pomíluj nás."),
("","","Svjatíji múčenicy, na zemlí podvíhšesja, mráz preterpíša, i ohňú predášasja, vodá ích priját. Ťích jésť hlás: proidóchom skvozí óhň i vódu, i izvedé ný v pokój. Ťích molítvami Bóže, pomíluj nás."),
("","","V múkach súšče svjatíji, rádujuščesja vopijáchu: kúpľa nám súť sijá ko Vladýci. Vmísto byvájuščich rán na ťilesích, svítloje oďijánije vo voskresénije procvitét nám, za bezčéstije vincý, za úzy temníčnyja ráj: i za jéže so zloďíji osuždénije, jéže so ánhely žitijé. Molítvami ích Hóspodi, spasí dúšy náša."),
("","","Tý sozdávyj mjá Hóspodi, i položí na mňí rúku tvojú, i zapovídav mí rékl jesí: v zémľu páki pójdeši. Nastávi mjá na právyj púť tvój, proščája mňí prehrišénija. Oslábi mí, i spasí mja, moľúsja, jáko čelovikoľúbec."),
("Bohoródičen","","Ole okajánnaja dušé! Kíj otvít ímaši reščí Sudijí vo ón čás, jehdá prestóly postávjatsja na suďí, i sudijá priídet ot nebés, sošéd so ťmámi ánheľskimi? Jehdá sjádet na sudíšči, prjú sotvoríti s rabý nepotrébnymi, podóbnymi mňí, čtó otviščáti ímaši? Čtóže prinestí tohdá? Poístinňi ničtóže, úm i ťílo oskvernívši tvojé. Ťímže pripadí k Ďívi, i zoví neprestánno, podáti tebí bohátno hrichóv proščénije."),
),
"ST": (
("","Rádujsja póstnikom","Svítom licá tvojehó Christé, prestávlenyja jáko ščédr prosvití. Vselí já v místo zláčno, pri vodách tvojehó čístaho i božéstvennaho pokója, v želájemych ňídrich Avraáma práotca, iďíže svít tvój čísťi sijájet, i prolivájutsja istóčnicy blahostýni: iďíže likújut jásno veseľáščesja právednych vsích sobóri o tvojéj bláhosti. S nímiže učiní rabý tvojá, podajá ím véliju mílosť."),
("","","Píti vsesostávnymi hlásy, slavoslóviti že tvojú deržávu, blahovolí ščédre, prestávľšyjasja ot privrémennych k tebí Vladýci vsích i Bóhu nášemu, podajá krasotóju tvojéju osviščátisja, i sládkaho i krásnaho pričástija tvojehó, vosprijáti že i naslaždátisja čísťíjše: iďíže ókrest prestóla tvojehó likújut ánheli, i svjatých lícy rádostno obstoját. S nímiže tvojím rabóm pokój podážď, i véliju mílosť."),
("","","Iďíže prorókov lík, apóstolov i múčenikov čínove, i vsí íže ot víka opravdívšijisja tvojéju spasíteľnoju strástiju i króviju, jéjuže iskupíl jesí pľinénaho čelovíka, támo víroju usópšyja upokój, jáko čelovikoľúbec, proščájaj sohrišénija: jedín bo bezhríšen na zemlí požíl jesí svját voístinnu, jedín vo uméršich svobóď. Ťímže tvojím rabóm pokój podážď, i véliju mílosť."),
("Bohoródičen","","Zakónom hrichóvnym nás poraboščénnych svobodíla jesí Vladýčice, v ložesnách zakonodávca i carjá Christá začénši jedína Ďívo Máti, ímže opravdájemsja túne, i blahodátiju : jehóže nýňi molí, dúšy víduščich ťá Bohomáter, napisáti v knízi živótňij, jáko da chodátajstvom tvojím spásšesja vseneporóčnaja, Sýna tvojehó ľubéznoje izbavlénije polúčim, tomú poklaňájuščesja, podajúščemu mírovi véliju mílosť."),
),
)
#let L = (
"B": (
("","","Razbójnik na kresťí Bóha ťá býti vírovav, Christé, ispovída ťá čísťi ot sérdca, pomjaní mja Hóspodi, vopijá, vo cárstviji tvojém."),
("","","Načalozlóbnaho vrahá, umérše múčenicy, pohubíste, i vzydóste k výšnim, vinčávšesja božéstvennymi pobídami, i carjú vsích Bóhu predstáste."),
("","","Svjaščénstva svítom svjatítelije prosviščájemi proslávišasja, i prepodóbnych mnóžestvo prisnosúščnyj polučíša živót: ťímže ublažájemi súť."),
("","","S líki izbránnych na mísťi Vladýko oslablénija, íchže prestávil jesí, vselí Slóve, prezrív Christé, jáže na zemlí ťích sohrišénija."),
("","","O Tróice čéstnája! svjatítelej i múčenik čéstných pódvihi umoléna búdi: víroju uméršich dušám spasénije dáruj, i véliju mílosť."),
("","","Jáže nevmistímaho vsími, Bohorádovannaja vmistíla jesí, i róždši páče jestestvá i slóva, tohó mílostiva býti vsím Vladýčice umolí."),
),
)
|
|
https://github.com/wizicer/gnark-cheatsheet | https://raw.githubusercontent.com/wizicer/gnark-cheatsheet/main/README.md | markdown | # Gnark Cheatsheet
This cheatsheet is based on `gnark v0.10.0`.
![preview][png]
# Download
You can download the cheatsheet in following formats:
- [PDF][pdf]
- [typst][typst]
Please [file an issue][issues] if you have ideas for improvement or find mistakes.
# License [![Creative Commons License][by-img]][by]
The gnark cheatsheet comes with a [Creative Commons Attribution 4.0 International License][by].
[pdf]: gnark-cheatsheet.pdf
[png]: preview.png
[typst]: gnark-cheatsheet.typ
[by]: https://creativecommons.org/licenses/by/4.0/
[by-img]: https://i.creativecommons.org/l/by/4.0/88x31.png
[issues]: https://github.com/wizicer/gnark-cheatsheet/issues |
|
https://github.com/typst/packages | https://raw.githubusercontent.com/typst/packages/main/packages/preview/tidy/0.1.0/src/styles.typ | typst | Apache License 2.0 |
#import "styles/default.typ"
#import "styles/minimal.typ"
|
https://github.com/ivaquero/book-control | https://raw.githubusercontent.com/ivaquero/book-control/main/Toolbox-Practice.typ | typst | #import "@local/scibook:0.1.0": *
#show: doc => conf(
title: "MATLAB 工具箱最佳实践",
author: ("ivaquero"),
header-cap: "现代控制理论",
footer-cap: "github@ivaquero",
outline-on: false,
doc,
)
= 工程结构
<tree>
== 根目录
<root>
根目录即工程目录,通常采用驼峰命名,如 `quickerSimCFD`。其大体结构如下
```markdown
quickerSimCFD/
| README.md
| LICENSE
└───images/
readmeImage.png
```
== 工具箱目录
<toolbox>
工具箱目录即算法代码目录,其应包括如下文件
- 算法接口文件:如`add.m`
- 算法底层文件夹:`internal`
- 交互教程文件:`gettingStarted.mlx`
- 示例文件夹:`examples`
其大体结构如下
```markdown
quickerSimCFD/
:
└───toolbox/
| add.m
| gettingStarted.mlx
├───examples/
| usingAdd.mlx
└───internal/
intToWord.m
```
== 增强
<enhancing>
MATLAB 提供了各种功能,以使工具箱更直观,更方便使用。推荐实践有:
=== [参数验证]
为增强用户的使用功能时的经验,我们可以添加一个“arguments”块创建定制的选项卡完成建议(R2019a 引入)。此外,MATLAB 将验证类型,大小和值传递给我们的功能,使用户可以调用我们的功能正确。请参阅:#link("https://www.mathworks.com/help/matlab/matlab_prog/function-argument-validation-1.html")[Function-Argument-Validation]。
若我们需要对选项卡完成的更多控制权,请创建一个`functionsignatures.json`,然后将其与相应的函数或类相同的目录中。请参阅:#link("https://www.mathworks.com/help/matlab/matlab_prog/customize-code-suggestions-and-completions.html")[Customize-Code-Suggestions-And-Completions]。
=== 命名空间
名称空间(也称为软件包)提供了一种组织类和功能的方法,并降低了具有相同名称的两个功能的风险。请参阅:#link("https://www.mathworks.com/help/matlab/matlab_oop/scoping-classes-with-packages.html")
=== MATLAB Apps
MATLAB 应用程序是交互式图形应用程序,允许用户在工具箱中执行特定的工作流程。我们将 MATLAB 应用程序包装到一个文件(.mlapp)中,以更轻松地分发。在工具箱文件夹的顶层创建“应用程序”文件夹。打包工具箱时,请确保将我们的应用程序包含在工具箱包装对话框的应用程序部分中。这样,用户可以在安装后轻松访问和运行我们的应用程序。请参阅:#link("https://www.mathworks.com/help/matlab/gui-development.html")[GUI-Development]。
=== 实时任务
实时任务是简单的点击接口,可以在 R2022a 开始的实时脚本中使用。它们为用户提供了一种交互式和直观的方法,可以与我们的工具箱进行交互。将实时任务类放在工具箱文件夹中的“内部”文件夹中,因为用户不直接调用此功能。作为创建的一部分,我们将创建一个 `liveTasks.json` 文件,该文件必须在 `resources` 文件夹中。请参阅:#link("https://www.mathworks.com/help/matlab/develop-live-editor-tasks.html")[Develop-Live-Editor-Tasks]。
== 总结
当使用了以上所有这些推荐功能,则我们的工具箱还应包括:
+ 对功能的选项卡完成和参数验证
+ Apps:`quickerSimCFD.mlapp`
+ 命名空间`describe`中的次级功能:`+describe/describe.add`
+ 实时任务:`internal/liveTasks.json`
此时工程结构为
```markdown
quickerSimCFD/
:
└───toolbox/
| add.m
| functionSignatures.json
| gettingStarted.mlx
├───+describe/
| add.m
├───apps/
| quickerSimCFD.mlapp
├───examples/
| usingAdd.mlx
└───internal/
| addLiveTask.m
| intToWord.m
└───resources/
liveTasks.json
```
#pagebreak()
= 打包
<packaging>
共享 MATLAB 工具箱通常涉及共享`.m`文件的集合或将它们组合到`.zip`文件中。但是,这里强烈建议一种更好的方法,即将工具箱包装到 MATLAB 工具箱文件中(`.mltbx`)从而获得更增强的用户体验。
我们可以为工具箱添加版本编号和其他信息提供图标。用户可以通过 #link("https://www.mathworks.com/help/matlab/matlab_env/get-add-ons.html")[Add-on Manager] 轻松发现,安装,更新和卸载工具箱。请参阅:#link("https://www.mathworks.com/help/matlab/matlab_prog/create-and-share-custom-matlab-toolboxes.html")[Create-And-Share-Custom-Matlab-Toolboxes]。
另外,建议命名包装文件 `toolboxPackaging.prj` 并命名图标文件为`toolboxPackaging.png`,将其放入`images`文件夹中。
使用 `Toolbox Packaging Tool` 创建工具箱包装文件。在 MATLAB,转到 `Home` 选项卡的`Add-Ons`菜单,选择`Toolbox Packaging Tool`。
#figure(
image("images/matlab-toolbox.png", width: 45%),
// caption: "",
// supplement: [图]
)
== 打包文件
`Toolbox Packaging Tool` 创建的 MATLAB 工具箱文件(`.mltbx`)应放在根目录下方的名为 `release` 的文件夹中。从此是一个派生文件,不应在源控制下。此时的工程结构如下:
```markdown
quickerSimCFD/
:
| toolboxPackaging.prj
├───images/
│ readmeImage.png
│ toolboxPackaging.png
├───release/
│ Arithmetic Toolbox.mltbx
└───toolbox/
add.m
:
```
== 发布策略
打包完成后,我们有多个选择发布我们的工具箱
- 创建一个 #link("https://docs.github.com/en/repositories/releasing-projects-on-github/managing-releases-in-a-repository")[GitHub 仓库],并链接到 #link("https://www.mathworks.com/matlabcentral/fileexchange/")[MATLAB File Exchange]。工具箱将在 `Add-on Explorer` 中出现,并将安装最新的发布版本。请参阅 #link("https://www.mathworks.com/matlabcentral/discussions/highlights/132204-github-releases-in-file-exchange")[Github-Releases-In-File-Exchange]。
- 将工具箱文件(`.mltbx`)复制到用户共享位置,双击它以安装它。
== 维护
<robust>
=== 测试
<tests>
测试检查工具箱的质量并帮助我们建立信心高质量的发布。#link("https://www.mathworks.com/help/matlab/matlab-unit-test-framework.html")[MATLAB Testing Framework] 提供了用于测试代码的支持。对于熟悉 MATLAB 的用户,应该很熟悉#link("https://www.mathworks.com/help/matlab/function-based-unit-tests.html")[Function-Based Unit Tests]。
将测试放在 `tests` 文件夹中。若在 GitHub 上托管工具箱,则可以使用 #link("https://github.com/matlab-actions/overview")[GitHub Actions] 来通过自动运行测试来限定更改。
现在,我们的工程结构为
```markdown
quickerSimCFD/
:
├───tests/
| testAdd.m
| testIntToWord.m
└───toolbox/
add.m
:
```
#pagebreak()
== 工程文件
<project>
#link("https://www.mathworks.com/help/matlab/projects.html")[工程文件] 是确保创作团队保持一致环境的好方法。它管理复杂项目中的依赖性,使路径正确,并与源控制系统集成。
使项目文件(带有`.prj`扩展名)与根目录相同的名称。将其放入根目录中。可得
```markdown
quickerSimCFD/
| README.md
| quickerSimCFD.prj
| license.txt
| toolboxPackaging.prj
:
└───resources/
```
== 持续集成
<cicd>
源控制系统应使用此文件夹作为源存储库的根。包括`.gitatributes`和`.gitignore`。一个典型 MATLAB 工具箱项目的 `.gitignore` 文件可参考 #link("https://github.com/mathworks/gitignore/blob/main/Global/MATLAB.gitignore")。
与打包有关的脚本应放置在根文件夹下方的`buildUtilities`文件夹中。 考虑使用 R2022b 中引入的 #link("https://www.mathworks.com/help/matlab/matlab_prog/overview-of-matlab-build-tool.html")[buildtool]。与 `buildtool` 关联的任务功能在 `buildfile.m` 中。
```markdown
quickerSimCFD/
│ .gitattributes
│ .gitignore
| README.md
| quickerSimCFD.prj
| buildfile.m
| license.txt
| toolboxPackaging.prj
├───.git/
:
├───resources/
└───buildUtilities/
```
== 在线运行
<online>
#link("https://www.mathworks.com/products/matlab-online/git.html")[MATLAB Online] 给出了在线运行
MATLAB 的方法。这为访问我们的 GitHub 仓库的用户提供了一种简单的方法,可以在文件交换时跳到我们的代码。设置`File Exchange`条目后,我们的工具箱将出现在页面顶部的工具。请参阅 #link("https://blogs.mathworks.com/community/2019/11/27/a-github-badge-for-the-file-exchange/")[Github-Badge-For-The-File-Exchange]。
|
|
https://github.com/TypstApp-team/typst | https://raw.githubusercontent.com/TypstApp-team/typst/master/tests/typ/meta/cite-form.typ | typst | Apache License 2.0 | // Test citation forms.
---
#set page(width: 200pt)
Nothing: #cite(<arrgh>, form: none)
#cite(<netwok>, form: "prose") say stuff.
#bibliography("/files/works.bib", style: "apa")
|
https://github.com/jgm/typst-hs | https://raw.githubusercontent.com/jgm/typst-hs/main/test/typ/math/matrix-alignment-01.typ | typst | Other | // Test alternating explicit alignment in a matrix.
$ mat(
"a" & "a a a" & "a a";
"a a" & "a a" & "a";
"a a a" & "a" & "a a a";
) $
|
https://github.com/kilpkonn/msc-thesis | https://raw.githubusercontent.com/kilpkonn/msc-thesis/master/main.typ | typst | #import "template.typ": *
#show: project.with(
title: "Term Search in Rust",
title_estonian: "Avaldise otsing programmeerimiskeeles Rust",
thesis_type: "Master's thesis",
thesis_type_estonian: "Magistritöö",
authors: (
(
name: "<NAME>",
student_code: "211564IAPM"
),
),
supervisors: (
(
name: "<NAME>",
degree: "MSc",
),
),
location: "Tallinn",
date: "May 12, 2024",
dev: false,
)
= Introduction
Rust#cite-footnote("Rust", "2024-04-06", "https://www.rust-lang.org/", "https://web.archive.org/web/20240409193051/https://www.rust-lang.org/") is a programming language for developing reliable and efficient systems.
The language was created by <NAME>, later developed at Mozilla for Firefox, but is now gaining popularity and has found its way to the Linux kernel#cite-footnote("Linux 6.1-rc1", "2024-04-06", "https://lkml.org/lkml/2022/10/16/359", "https://web.archive.org/web/20240408110623/https://lkml.org/lkml/2022/10/16/359").
It differs from other popular systems programming languages such as C and C++ by focusing more on the reliability and productivity of the programmer.
Rust has an expressive type system that guarantees a lack of undefined behavior at compile type.
It is done with a novel ownership model and is enforced by a compiler tool called borrow checker.
The borrow checker rejects all programs that may contain illegal memory accesses or data races.
We will call the set of programs that can be compiled valid, as they are guaranteed to not cause undefined behavior.
Many programming languages with type systems that guarantee the program to be valid have tools that help the programmer with term search i.e. by searching for valid programs (usually called expressions in Rust) that satisfy the type system.
Rust, however, does not have tools for term search, although the type system makes it a perfect candidate for one.
Consider the following Rust program in @into-example-1:
#figure(
sourcecode()[
```rs
enum Option<T> { None, Some(T) }
fn wrap(arg: i32) -> Option<i32> {
todo!();
}
```],
caption: [
Rust function to wrap `i32` in `Option`
],
) <into-example-1>
From the types of values in scope and constructors of ```rust Option```, we can produce the expected result for ```rust todo!()``` by applying the constructor ```rust Some``` to ```rust arg``` and returning it.
By combining multiple constructors for types as well as functions in scope or methods on types, it is possible to produce more complex, valid programs.
== Motivation
Due to Rust's expressive type system, programmers might find themselves quite often wrapping the result of some function behind multiple layers of constructors. For example, in the web backend framework `actix-web`#cite-footnote("Actix", "2024-04-06", "https://actix.rs/", "https://web.archive.org/web/20240329223953/https://actix.rs/"), a typical JSON endpoint function might look something like shown in @motivation-example-1.
#figure(
sourcecode()[
```rs
struct FooResponse { /* Struct fields */ }
#[get("/foo")]
async fn foo() -> Option<Json<FooResponse>> {
let service_res = service.foo(); // Get a response from some service
Some(Json(FooResponse {
/* Fill struct fields from `service_res` */
}))
}
```],
caption: [
Example endpoint in `actix-web` framework
],
) <motivation-example-1>
We can see that converting the result ```rust service_res``` from the service to ```rust FooResponse``` and wrapping it in ```rust Some(Json(...))``` can be automatically generated just by making the types match.
This means that term search can be used to reduce the amount of code the programmer has to write.
When investigating common usage patterns among programmers using large language models for code generation, @how-programmers-interact-with-code-generation-models[p. 19] found two patterns:
1. Language models are used to reduce the amount of code the programmer has to write therefore making them faster.
They call it the _acceleration mode_.
2. Language models are used to explore possible ways to complete incomplete programs.
This is commonly used when a programmer is using new libraries and is unsure how to continue.
They call this usage pattern _exploration mode_.
We argue that the same patterns can be found among programmers using term search.
In acceleration mode, term search is not as powerful as language models, but it can be more predictable as it has well-defined tactics that it uses rather than deep neural networks.
There is not so much "wow" effect - it just produces code that one could write by trying different programs that type-check.
However, we expect term search to perform well in _exploration mode_.
@how-programmers-interact-with-code-generation-models[p. 10] finds that programmers tend to explore only if they have confidence in the tool.
As term search only produces valid programs based on well-defined tactics, it is a lot easier to trust it than code generation based on language models that have some uncertainty in them.
== Research Objectives
The main objective of this thesis is to implement a tactics-based term search for the programming language Rust.
The algorithm should:
- only produce valid programs, i.e. programs that compile
- finish fast enough to be used interactively while typing
- produce suggestions for a wide variety of Rust programs
- not crash or cause other issues on any Rust program
Other objectives include:
- Evaluating the fitness of tactics on existing large codebases
- Investigating term search usability for auto-completion
== Contributions of the thesis
In this thesis, we make the following contributions:
- @background gives an overview of term search algorithms used in other languages and autocompletion tools used in Rust and mainstream programming languages. We also introduce some aspects of the Rust programming language that are relevant to the term search.
- @design introduces term search to Rust by extending the official language server of the Rust programming language, `rust-analyzer`.
We discuss the implementation of the algorithm in detail as well as different use cases.
In @tactics, we describe the capabilities of our tool.
- @evaluation evaluates the performance of the tool. We compare it to mainstream tools, some machine-learning-based methods and term search tools in other programming languages.
- @future-work describes future work that would improve our implementation. This includes technical challenges but also describes possible extensions to the algorithm.
We have upstreamed our implementation of term search to the `rust-analyzer` project.
It is part of the official distribution since version `v0.3.1850`#cite-footnote("Rust Analyzer Changelog #221", "2024-04-06", "https://rust-analyzer.github.io/thisweek/2024/02/19/changelog-221.html", "https://web.archive.org/web/20240412220709/https://rust-analyzer.github.io/thisweek/2024/02/19/changelog-221.html"), released on February 19th 2024.
An archived version can be found at the Software Heritage Archive #link("https://archive.softwareheritage.org/browse/revision/6b250a22c41b2899b0735c5bc607e50c3d774d74/?origin_url=https://github.com/kilpkonn/rust-analyzer&snapshot=25aaa3ceeca154121a5c2944f50ec7b17819a315")[`swh:1:rev:6b250a22c41b2899b0735c5bc607e50c3d774d74`].
= Background <background>
In this chapter, we will take a look at the type system of the Rust programming language to understand the context of our task.
Next, we will take a look at what the term search is and how it is commonly used.
Later, we will study some implementations for term search to better understand how the algorithms for it work.
In the end, we will briefly cover how _autocompletion_ is implemented in modern tools to give some context of the framework we are working in and the tools that we are improving on.
== The Rust language
Rust is a general-purpose systems programming language first released in 2015#cite-footnote("Announcing Rust 1.0", "2024-04-06", "https://blog.rust-lang.org/2015/05/15/Rust-1.0.html", "https://web.archive.org/web/20240406065426/https://blog.rust-lang.org/2015/05/15/Rust-1.0.html").
It takes lots of inspiration from functional programming languages, namely, it supports algebraic data types, higher-order functions, and immutability.
=== Type system
Rust has multiple different kinds of types.
There are scalar types, references, compound data types, algebraic data types, function types, and more.
In this section, we will discuss types that are relevant to the term search implementation we are building.
We will ignore some of the more complex data types such as function types as implementing term search for them is out of the scope of this thesis.
Scalar types are the simplest data types in Rust.
A scalar type represents a single value.
Rust has four primary scalar types: integers, floating-point numbers, booleans, and characters.
Compound types can group multiple values into one type.
Rust has two primitive compound types: arrays and tuples.
An array is a type that can store a fixed amount of elements of the same type.
Tuple, however, is a type that groups values of different types.
Examples for both array and tuple types can be seen in @rust-types on lines 2 and 3.
Reference types are types that contain no other data than a reference to some other type.
An example of a reference type can be seen in @rust-types on line 4.
#figure(
sourcecode()[```rs
let a: i32 = 0; // Scalar type for 32 bit signed integer
let b: [u8, 3] = [1, 2, 3]; // Array type that stores 3 values of type `u8`
let c: (bool, char, f32) = (true, 'z', 0.0); // Tuple that consists of 3 types
let d: &i32 = &a; // Reference type to `i32`
```],
caption: [
Types in Rust
],
) <rust-types>
Rust has two kinds of algebraic types: _structures_ (also referred as `struct`s) and _enumerations_ (also referred as `enum`s).
Structures are product types, and enumerations are sum types.
Each of them comes with their own data constructors.
Structures have one constructor that takes arguments for all of its fields.
Enumerations have one constructor for each of their variants.
Both of them are shown in @rust-type-constructor.
#figure(
sourcecode()[```rs
// Product type has values for both `x` and `y`
struct Foo {
x: i32,
y: bool,
}
// Sum type has values for either constructor `A` or `B`
enum Bar {
A(i32),
B(bool),
}
fn main() {
let foo = Foo { x: 1, y: true }; // Initialize struct
let bar = Bar::B(false); // Initialize enum with one of it's variants
}
```],
caption: [
Sum and product types in Rust
],
) <rust-type-constructor>
To initialize a `struct`, we have to provide terms for each of the fields it has, as shown on line 12.
For `enum`, we choose one of the variants we wish to construct and only need to provide terms for that variant.
Note that structures and enumeration types may both depend on generic types, i.e. types that are specified at the call site rather than being hard-coded to the type signature.
For example, in @rust-type-constructor-generics, we made the struct ```rust Foo``` generic over `T` by making the field `x` be of generic type `T` rather than some concrete type.
A common generic enum in Rust is the ```rust Option``` type which is used to represent optional values.
The ```rust None``` constructor takes no arguments and indicates that there is no value.
Constructor ```rust Some(T)``` takes one term of type `T` and indicates that there is some value stored in `Option`.
Initializing structs and enums with different types is shown in the `main` function at the end of @rust-type-constructor-generics.
#figure(
sourcecode()[```rs
struct Foo<T> {
x: T,
y: bool,
}
enum Option<T> {
Some(T),
None,
}
fn main() {
let foo_bool: Foo<bool> = Foo { x: true, y: true};
let foo_int: Foo<i32> = Foo { x: 123, y: true};
let option_str: Option<&str> = Some("some string");
let option_bool: Option<bool> = Some(false);
}
```],
caption: [
Sum and product types with generics
],
) <rust-type-constructor-generics>
=== Type unification
It is possible to check for either syntactic or semantic equality between the two types.
Two types are syntactically equal if they have the same syntax.
Syntactic equality is a very restrictive way to compare types.
A much more permissive way to compare types is semantic equality.
Semantic equality of types means that two types contain the same information and can be used interchangeably.
Using syntactic equality to compare types can cause problems.
Rust high-level intermediate representation (HIR) has multiple ways to define a type.
This means that the same type can be defined in multiple ways that are not syntactically equal.
For example, in the program ```rust type Foo = i32```, the type ```rust Foo``` and the type ```rust i32``` are not syntactically equal.
However, they are semantically equal, as ```rust Foo``` is an alias for ```rust i32```.
This means that the types unify even though they are syntactically different.
To check for semantic equality of types we see if two types can be unified.
Rust's type system is based on a Hindley-Milner type system @affine-type-system-with-hindley-milner, therefore the types are compared in a typing environment.
In Rust, the _trait solver_ is responsible for checking the unification of types#cite-footnote("Rust Compiler Development Guide, The ty module: representing types", "2024-04-06", "https://rustc-dev-guide.rust-lang.org/ty.html", "https://web.archive.org/web/20231205205735/https://rustc-dev-guide.rust-lang.org/ty.html").
The trait solver works at the HIR level of abstraction, and it is heavily inspired by Prolog engines.
The trait solver uses "first-order hereditary harrop" (FOHH) clauses, which are Horn clauses that are allowed to have quantifiers in the body @proof-procedure-for-the-logic-of-hereditary-harrop-formulas.
Unification of types `X` and `Y` is done by registering a new clause `Unify(X, Y)` (the #emph[goal]) and solving for it.
Solving is done by a Prolog-like engine, which tries to satisfy all clauses registered in the typing environment.
If a contradiction is found between the goal and the clauses, there is no solution, and the types `X` and `Y` do not unify.
If a solution is found, it contains a set of subgoals that still need to be proven.
If we manage to recursively prove all the subgoals, then we know that `X` and `Y` unify.
If some goals remain unsolved but there is also no contradiction, then simply more information is needed to guarantee unification.
How we treat the last case depends on the use case, but in this thesis, for simplicity, we assume that the types do not unify.
An example of unification can be seen in @rust-type-unification.
#figure(
sourcecode(highlighted: (14,))[
```rs
trait HasAnswer {
type Answer;
fn get_answer(&self) -> Self::Answer;
}
struct Life { /* fields */ }
impl HasAnswer for Life {
type Answer = u8;
fn get_answer(&self) -> Self::Answer { 42 }
}
fn main() {
let life = Life { /* fields */ };
let ans: u8 = life.get_answer();
assert!(ans == 42);
}
```],
caption: [
A unification problem for the return type of `life.get_answer()`.
The goal is#linebreak()`Unify(<Life as HasAnswer>::Answer, u8)`.
In context is `Implemented(Life: HasAnswer)` and `AliasEq(<Life as HasAnswer>::Answer = u8)`.
From these clauses, we can solve the problem.
],
) <rust-type-unification>
=== Borrow checking
Another crucial step for the Rust compiler is borrow checking#cite-footnote("Rust Compiler Development Guide, MIR borrow check", "2024-04-06", "https://rustc-dev-guide.rust-lang.org/borrow_check.html", "https://web.archive.org/web/20230324181544/https://rustc-dev-guide.rust-lang.org/borrow_check.html").
The main responsibilities of the borrow checker are to make sure that:
- All variables are initialized before being used
- No value is moved twice or used after being dropped
- No value is moved while borrowed
- No immutable variable can be mutated
- There can be only one mutable borrow
Some examples of kinds of bugs that the borrow checker prevents are _use-after-free_ and _double-free_
The borrow checker works at the Middle Intermediate Representation (MIR) level of abstraction.
The currently used model for borrows is Non-Lexical Lifetimes (NLL).
The borrow checker first builds up a control flow graph to find all possible data accesses and moves.
Then it builds up constraints between lifetimes.
After that, regions for every lifetime are built up.
A region for a lifetime is a set of program points at which the region is valid.
The regions are built up from constraints:
- A liveness constraint arises when some variable whose type includes a region R is live at some point P. This simply means that the region R must include point P.
- Outlives constraint ```rust 'a: 'b``` means that the region of ```rust 'a``` has to also be a superset of the region of ```rust 'b```.
From the regions, the borrow checker can calculate all the borrows at every program point.
An extra pass is made over all the variables, and errors are reported whenever aliasing rules are violated.
Rust also has a concept of two-phased borrows that splits the borrow into two phases: reservation and activation.
These are used to allow nested function calls like ```rust vec.push(vec.len())```.
These programs would otherwise be invalid, as in the example above ```rust vec.len()``` is immutably borrowed while ```rust vec.push(...)``` takes the mutable borrow.
The two-stage borrows are treated as follows:
- It is checked that no mutable borrow conflicts with the two-phase borrow at the reservation point (`vec.len()` for the example above).
- Between the reservation and the activation point, the two-phase borrow acts as a shared borrow.
- After the activation point, the two-phase borrow acts as a mutable borrow.
There is also an option to escape the restrictions of the borrow checker by using ```rust unsafe``` code blocks.
In an ```rust unsafe``` code block, the programmer has the sole responsibility to guarantee the validity of aliasing rules with no help from the borrow checker.
== Term search <term-search>
Term search is the process of generating terms that satisfy some type in a given context.
In automated theorem proving, this is usually known as proof search.
In Rust, we call it a term search, as we don't usually think of programs as proofs.
The Curry-Howard correspondence is a direct correspondence between computer programs and mathematical proofs.
The correspondence is used in proof assistants such as Coq and Isabelle and also in dependently typed languages such as Agda and Idris.
The idea is to state a proposition as a type and then prove it by producing a value of the given type, as explained in @propositions-as-types.
For example, if we have an addition on natural numbers defined in Idris as shown in @idirs-add-nat.
#figure(
sourcecode()[
```hs
add : Nat -> Nat -> Nat
add Z m = m
add (S k) m = S (add k m)
```],
caption: [
Addition of natural numbers in Idris
],
) <idirs-add-nat>
We can prove that adding any natural number `m` to 0 is equal to the natural number `m`.
For that, we create a declaration `add_zero` with the type of the proposition and prove it by defining a program that satisfies the type.
#figure(
sourcecode()[
```hs
add_zero : (m : Nat) -> add Z m = m -- Proposition
add_zero m = Refl -- Proof
```],
caption: [
Prove $0 + n = n$ in Idris
],
) <idirs-plus-reduces-z>
The example above is quite trivial, as the compiler can figure out from the definition of `add` that ```hs add Z m``` is defined to be `m` according to the first clause in the definition of `add`
Based on that we can prove `add_zero` by reflexivity.
However, if there are more steps required, writing proofs manually gets cumbersome, so we use tools to automatically search for terms that inhabit a type i.e. proposition.
For example, Agda has a tool called Agsy that is used for term search, and Idris has this built into its compiler.
=== Term search in Agda
Agda @dependently-typed-programming-in-agda is a dependently typed functional programming language and proof assistant.
It is one of the first languages that has sufficiently good tools for leveraging term search for inductive proofs.
We will be more interested in the proof assistant part of Agda, as it is the one leveraging the term search to help the programmer come up with proofs.
As there are multiple options, we picked two that seem the most popular or relevant for our use case.
We chose Agsy as this is the well-known tool that is part of the Agda project itself, and Mimer, which attempts to improve on Agsy.
==== Agsy <agsy>
Agsy is the official term-search-based proof assistant for Agda.
It was first published in 2006 in @tool-for-automated-theorem-proving-in-agda and integrated into Agda in 2009#cite-footnote("Agda, Automatic Proof Search (Auto)", "2024-04-06", "https://agda.readthedocs.io/en/v2.6.4.1/tools/auto.html", "https://web.archive.org/web/20240410183801/https://agda.readthedocs.io/en/v2.6.4.1/tools/auto.html").
We will be looking at the high-level implementation of its algorithm for term search.
In principle, Agsy iteratively refines problems into more subproblems until enough subproblems can be solved.
This process is called iterative deepening.
This is necessary as a problem may, in general, be refined to infinite depth.
The refinement of a problem can produce multiple branches with subproblems.
In some cases, we need to solve all the subproblems.
In other cases, it is sufficient to solve just one of the subproblems to solve the "top-level" problem.
An example where we need to solve just one of the subproblems is when we try different approaches to come up with a term.
For example, we can either use some local variable, function or constructor to solve the problem as shown in @agsy_transformation_branches.
#figure(
image("fig/agsy_transformation_branches.svg", width: 60%),
caption: [
Solving the top-level problem requires solving _at least one_ of the subproblems
],
) <agsy_transformation_branches>
In case we use constructors or functions that take multiple arguments, we need to solve all the subproblems of finding terms for arguments.
The same is true for case splitting: we have to solve subproblems for all the cases.
For example, shown in @agsy_all_branches we see that function ```hs foo : (A, B, C) -> Foo```
can only be used if we manage to solve the subproblems of finding terms of the correct type for all the arguments.
#figure(
image("fig/agsy_all_branches.svg", width: 60%),
caption: [
Solving the top-level problem requires solving _all_ of the subproblems
],
) <agsy_all_branches>
Agsy uses problem collections (```hs PrbColl```) to model the subproblems that need to be all solved individually for the "top-level" problem to be solved.
Solution collections (```hs SolColl```) are used to keep track of solutions for a particular problem collection.
A solution collection has a solution for each of the problems in a corresponding problem collection.
The intuition for the tool is the following:
1. Given a problem, we create a set of possible subproblem collections out of which we need to solve _at least one_, as shown in @agsy_transformation_branches.
2. We attempt to solve _all_ the subproblem collections by recursively solving all the problems in the collection
3. If we manage to solve _all_ the problems in the collection, we use it as a possible solution, otherwise, we discard it as a dead end.
The algorithm itself is based on depth-first search (DFS) and consists of two subfunctions.
Function ```hs search: Problem -> Maybe [Solution]``` is the main entry point that attempts to find a set of solutions for a problem.
The function internally makes use of another function ```hs searchColl: PrbColl -> Maybe [SolColl]``` that attempts to find a set of solution collections for a problem collection.
The pseudocode for the `search` and `searchColl` functions can be seen in @agsy-snippet.
We model Problem collections as a list of subproblems together with a _refinement_ that produces those problems.
A refinement is a recipe to transform the problem into zero or more subproblems.
For example, finding a pair ```hs (Bool, Int)``` can be refined to two subproblems: finding a term of type ```hs Bool``` and another of type ```hs Int``` and applying the tuple constructor ```hs (_,_)```.
If we refine the problem without creating any new subproblems, then we can call the problem solved.
Otherwise, all the subproblems need to be solved for the solution to hold.
The refinement is stored so that, on a successful solution, we can construct the term solving the top-level problem from the solution collection.
The `search` algorithm starts by refining the problem into new problem collections.
Refining is done by tactics.
Tactics are essentially just a way of organizing possible refinements.
An example tactic that attempts to solve the problem by filling it with locals in scope can be seen in @agsy-example-tactic.
In case refining does not create any new problem collections, the base case is reached, and the problem is trivially solved (line 9 in @agsy-snippet).
When there are new problem collections, we try to solve _any_ of them.
In case we cannot solve any of the problem collections, then the problem is unsolvable, and we give up by returning ```hs Nothing``` (line 15).
Otherwise, we return the solutions we found.
We solve problem collections by using the `searchColl` function.
Problem collections where we can't solve all the problems cannot be turned into solution collections as there is no way to build a well-formed term with problems remaining in it.
We only care about cases where we can fully solve the problem, so we discard them by returning ```hs Nothing```.
On line 14 of @agsy-snippet we filter out unsuccessful solutions.
For successful solution collections, we substitute the refinements we took into the problem to get back the solution.
The solution is a well-formed term with no remaining subproblems, which we can return to the callee.
#figure(
sourcecode()[```hs
newtype ProbColl = (Refinement, [Problem])
newtype SolColl = (Refinement, [Solution])
-- Find solutions to a problem
search :: Problem -> Maybe [Solution]
search p =
case (createRefs p) of
-- ↓ No new problems, trivially solved
[] -> Just [TrivialSolution]
-- ↓ Refinement created at least one subproblem
subproblems ->
-- Recursively solve subproblems; discard solution
-- collections that are not fully solved.
case (dropUnsolved $ map searchColl subproblems) of
[] -> Nothing
sols -> Just $ map (substitute p) sols
where
dropUnsolved :: [Maybe [SolColl]] -> [SolColl]
dropUnsolved = flatten . catMaybes
-- Find a solution to every problem in problem collection
searchColl :: ProbColl -> Maybe [SolColl]
searchColl = sequence $ fmap search
-- Create refinements for problem
createRefs :: Problem -> [ProbColl]
createRefs p = flatten [tactic1 p, tactic2 p, tacticN p]
-- Create a solution to a problem from a refinement
-- and solutions to subproblems.
substitute :: Problem -> SolColl -> Solution
substitute = {- elided -}
```],
caption: [
A high-level overview of the term search algorithm used in Agsy
],
) <agsy-snippet>
An example of a tactic can be seen in @agsy-example-tactic.
#figure(
sourcecode()[```hs
-- Suggest locals for solving any problem
tacticLocal :: Problem -> [ProbColl]
tacticLocal p =
let locals = localsInScope p
in
map (\l -> (Refinement::SubstituteLocal p l, [])) $
filter (\l -> couldUnify p l) locals
```
],
caption: [
An example tactic that attempts to solve the problem by using locals in scope
],
) <agsy-example-tactic>
As described above, the algorithm is built around DFS.
However, the authors of @tool-for-automated-theorem-proving-in-agda note that while the performance of the tool is good enough to be useful, it performs poorly on larger problems.
They suggest that more advanced search space reduction techniques can be used, as well as writing it in a language that does not suffer from automatic memory management.
It is also noted that there seem to be many false subproblems that can never be solved, so they suggest a parallel algorithm that could potentially prove the uselessness of those subproblems and reduce the search space.
#pagebreak()
==== Mimer
Mimer @mimer is another proof-assistant tool for Agda that attempts to address some of the shortcomings in Agsy.
As of February 2024, Mimer has become part of Agda#cite-footnote("Agda GitHub pull request, Mimer: a drop-in replacement for Agsy", "2024-04-06", "https://github.com/agda/agda/pull/6410", "https://web.archive.org/web/20240410183837/https://github.com/agda/agda/pull/6410") and will be released as a replacement for Agsy.
According to its authors, it is designed to handle many small synthesis problems rather than complex ones.
Mimer is less powerful than Agsy as it doesn't perform case splits.
On the other hand, it is designed to be more robust.
Other than not using case splits, the main algorithm follows the one used in Agsy and described in @agsy.
The main differences from the original Agsy implementation are:
1. Mimer uses memoization to avoid searching for the same term multiple times.
2. Mimer guides the search with branch costs.
Branch costs are a heuristic to hopefully guide the search to an answer faster than randomly picking branches.
Mimer gives lower costs to branches that contain more local variables and fewer external definitions.
The rationale for that is that it is more likely that the user wishes to use variables from the local scope than from outside of it.
However, they noted that the costs of the tactics need to be tweaked in future work, as this was not their focus.
=== Term search in Standard ML <standardml>
As a part of the RedPRL#cite-footnote("The red* family of proof assistants", "2024-04-06", "https://redprl.org/", "https://web.archive.org/web/20240316102035/https://redprl.org/") @redprl project, @algebraic-foundations-of-proof-refinement implements term search for Standard ML.
The algorithm suggested in @algebraic-foundations-of-proof-refinement keeps track of the subproblems in a telescope @telescopic-mappings-typed-lambda-calc.
A telescope is a list of types with dependencies between them.
It is a convenient data structure to keep the proof state for dependently typed languages.
However, for languages without dependent types (this also includes Rust), they suggest using a regular list instead.
To more effectively propagate substitutions to subproblems in the telescope @algebraic-foundations-of-proof-refinement suggests using BFS instead of DFS.
The idea is to run all the tactics once on each subproblem, repeatedly.
This way, substitutions propagate along the telescope of subproblems after every iteration.
In the case of DFS, we would propagate the constraints only after exhausting the search on the first subproblem in the sequence.
To better understand the difference between the BFS approach suggested and the DFS approach, let's see how each of them works.
First, let's consider the DFS approach as a baseline.
The high-level algorithm for DFS is to first generate possible ways to refine the problem into new subproblems and then solve each of the subproblems fully before continuing to the next subproblem.
In the snippet below, tactics create problem collections that are options we can take to refine the problem into new subproblems.
After that, we attempt to solve each set of subproblems to find the first problem collection where we manage to solve all the subproblems.
That problem collection effectively becomes our solution.
In @standardml-dfs-code we can see that the DFS fits functional style very well, as for all the subproblems, we can just recursively call the same `solve` function again.
Note that in the listing, the constraints are propagated to the remaining problems only after the problem is fully solved.
#figure(
sourcecode()[```hs
solve :: Problem -> Maybe Solution
solve problem =
let
pcs: [ProblemCollection] = tactics problem -- Generate possible refinements
in
-- Find only the first solution
head [combineToSolution x | Just x <- map solveDFS pcs]
solveDFS :: ProblemCollection -> Maybe SolutionCollection
solveDFS [] = Just [] -- No subproblems => Empty solution collection
solveDFS (p:ps) = do
sol <- solve p -- Return `Nothing` for no solution
ps' <- propagateConstraints sol ps -- Propagate constraints
rest <- solvesolveDFS ps' -- Attempt to solve other subproblems
return sol : rest
```],
caption: [
Pseudocode for DFS search
],
) <standardml-dfs-code>
Now let's look at how the BFS algorithm suggested in @algebraic-foundations-of-proof-refinement works.
The high-level algorithm for BFS is to generate possible ways to refine the problem into new subproblems and then incrementally solve all the subproblems in parallel.
The pseudocode for it can be seen in @standardml-bfs-code.
The algorithm starts by converting the given problem to a singleton problem collection.
Now the produced collection is fed into `solveBFS` function, which starts incrementally solving the problem collections.
In this example, we are using a queue to keep track of the problem collections we are solving.
Internally, the `solveBFS` function loops over the elements of the queue until either a solution is found or the queue becomes empty.
In the snippet, we check the status of the problem collection with a `status` function that tells us the status of the problem collection.
The status is either:
- *AllSolved* for problem collections that do not have any unresolved subproblems in them and are ready to be converted into solutions.
- *NoSolution* for problem collections that have remaining unresolved subproblems that we are unable to make any progress on.
- *RemainingProblems* for all the problem collections that we can make progress on by incrementally stepping the problem further.
In the case of ```hs AllSolved``` we return the solution as we are done with the search.
In the case of ```hs NoSolution``` we discard the problem from the queue.
Otherwise, (in the case of ```hs RemainingProblems```) we step the problem collection at the head of the queue and push the results back to the back of the queue.
Now we are ready to keep iterating the loop again with the new problem collection at the head of the queue.
Stepping the problem collection steps (or adds atomic refinements) to all problems in the problem collection and propagates the constraints to the rest of the subproblems if refinements produce any new constraints.
As the problem can generally be refined in multiple ways, the function returns a list of problem collections that are all possible successors to the input problem collection.
Propagating the constraints is done in the `propagateConstraints` function.
The function adds new constraints arising from the head element refinements to all subproblems in the problem collection.
#figure(
sourcecode()[```hs
solve :: Problem -> Maybe Solution
solve problem =
let
pcs: [ProblemCollection] = toSingletonCollection problem
in
fmap combineToSolution (solveBFS pcs) -- Find the first solution
solveBFS :: [ProblemCollection] -> Maybe SolutionCollection
solveBFS pcs =
loop (toQueue pcs)
where
loop :: Queue ProblemCollection -> Maybe SolutionCollection
loop [] = Nothing -- Empty queue means we didn't manage to find a solution
loop (pc:queue) = do
case status pc of
AllSolved -> return toSolutionCollection ps' -- Solution found
NoSolution -> loop queue -- Unable to solve, discard
RemainingProblems -> -- Keep iteratively solving
let
pcs: [ProblemCollection] = step pc
queue': Queue ProblemCollection = append queue pcs
in
loop queue'
step :: ProblemCollection -> [ProblemCollection]
step [] = []
step (p:ps) =
let
pcs: [ProblemCollection] = tactics p -- Possible ways to refine head
in
-- Propagate constraints and step other goals
flatten . map (\pc ->
step $ propagateContstraints ps (extractConstraints pc)) pcs
propagateConstraints :: ProblemCollection -> Constraints -> ProblemCollection
propagateConstraints ps constraints = fmap (addConstraints constraints) ps
```],
caption: [
Pseudocode for BFS search
],
) <standardml-bfs-code>
Consider the example where we are searching for a goal ```hs ?goal :: ([a], a -> String)``` that is a pair of a list of some type and a function of that type to `String`.
Similar goals in everyday life could arise from finding a list together with a function that can map the elements to strings to print them (`show` function).
Note that in this example, we want the first member of the pair to be a list, but we do not care about the types inside the list.
The only requirement is that the second member of the pair can map the same type to ```hs String```.
We have the following items in scope:
```hs
bar : Bar
mk_foo : Bar -> Foo
mk_list_foo : Foo -> [Foo]
mk_list_bar : Bar -> [Bar]
show_bar : Bar -> String
```
To simplify the notation, we name the goals as ```hs ?<number>```, for example, ```hs ?1``` for goal 1.
First, we can split the goal of finding a pair into two subgoals: ```hs [?1 : [a], ?2 : a -> String]```.
This is the same step for BFS and DFS, as there is not much else to do with ```hs ?goal``` as there are now functions
that take us to a pair of any two types except using the pair constructor.
At this point, we have two subgoals to solve
```hs
(?1 : [a], ?2 : a -> String)
```
Now we are at the point where the differences between DFS and BFS start playing out.
First, let's look at how the DFS would handle the goals.
We start by focusing on ```hs ?1```.
We can use `mk_list_foo` to transform the goal into finding something of the type ```hs Foo```.
Now we have the following solution and goals:
```hs
(mk_list_foo(?3 : Foo), ?2 : a -> String)
```
Note that although the `a` in ```hs ?s2``` has to be of type ```hs Foo```, we have not propagated this knowledge there yet as we are focusing on ```hs ?3```.
We only propagate the constraints when we discard the hole as filled.
We use `mk_foo` to create a new goal ```hs ?4 : Bar``` which we solve by providing `bar`.
Now we propagate the constraints to the remaining subgoals, ```hs ?2``` in this example.
This means that the second subgoal becomes ```hs ?2 : Foo -> String``` as shown below.
```hs
(mk_list_foo(mk_foo(?4 : Bar), ?2 : a -> String)
(mk_list_foo(mk_foo(bar)), ?2 : Foo -> String)
```
However, we cannot find anything of type ```hs Foo -> String``` so we have to revert to ```hs ?1```.
This time we use `mk_list_bar` to fill ```hs ?1``` meaning that the remaining subgoal becomes ```hs ?2 : Bar -> String```.
We can fill it by providing `show_bar`.
As no more subgoals are remaining the problem is solved with the steps shown below.
```hs
(mk_list_bar(?3 : Bar), ?2 : a -> String)
(mk_list_bar(bar), ?2 : Bar -> String)
(mk_list_bar(bar), show_bar)
```
An overview of all the steps we took can be seen in the @standardml-dfs-steps.
#figure(
sourcecode()[```hs
?goal : ([a], a -> String)
(?1 : [a], ?2 : a -> String)
(mk_list_foo(?3 : Foo), ?2 : a -> String)
(mk_list_foo(mk_foo(?4 : Bar), ?2 : a -> String)
(mk_list_foo(mk_foo(bar)), ?2 : Foo -> String) -- Revert to ?1
(mk_list_bar(?3 : Bar), ?2 : a -> String)
(mk_list_bar(bar), ?2 : Bar -> String)
(mk_list_bar(bar), show_bar)
```],
caption: [
DFS algorithm steps
],
) <standardml-dfs-steps>
Now let's take a look at the algorithm that uses BFS to handle the goals.
The first iteration is the same as described above, after which we have two subgoals to fill.
```hs
(?1 : [a], ?2 : a -> String)
queue = [[?1, ?2]]
```
As we are always working on the head element of the queue, we are still working on ```hs ?1```.
Once again, we use `mk_list_foo` to transform the first subgoal to ```hs ?3 : Foo```, but this time we also insert another problem collection into the queue, where we use `mk_list_bar` instead.
We also propagate the information to other subgoals so that we constrain ```hs ?2``` to either ```hs Foo -> String``` or ```hs Bar -> String```.
```hs
(mk_list_foo(?3 : Foo), ?2 : Foo -> String)
(mk_list_bar(?4 : Bar), ?2 : Bar -> String)
queue = [[?3, ?2], [?4, ?2]]
```
In the next step, we search for something of type ```hs Foo``` for ```hs ?3``` and a function of type ```hs Foo -> String``` in ```hs ?2```.
We find `bar` for the first goal, but not anything for the second goal.
This means we discard the branch as we are not able to solve the problem collection.
Note that at this point we still have ```hs ?4``` pending, meaning we have not yet exhausted the search in the current "branch".
Reverting now means that we save some work that was guaranteed to not affect the overall outcome.
The search space becomes
```hs
(mk_list_foo(mk_foo(?4 : Bar)), ?2 : <impossible>) -- discarded
(mk_list_bar(?4 : Bar), ?2 : Bar -> String)
queue = [[?4, ?2]]
```
Now we focus on the other problem collection.
In this iteration, we find solutions for both of the goals.
As all the problems in the problem collection get solved, we can turn the problem collection into a solution and return it.
```hs
(mk_list_bar(?5 : Bar), ?2 : Bar -> String)
(mk_list_bar(bar), show_bar)
```
An overview of all the steps we took can be seen in @standardml-bfs-steps.
Note that from line 3 to line 5, there are two parallel branches, and the order between branches is arbitrary.
#figure(
sourcecode()[```hs
?goal : ([a], a -> String)
(?1 : [a], ?2 : a -> String)
(mk_list_foo(?3 : Foo), ?2 : Foo -> String) -- Branch 1
(mk_list_foo(mk_foo(?4 : Bar)), ?2 : <impossible>) -- Discard branch 1
(mk_list_bar(?5 : Bar), ?2 : Bar -> String) -- Branch 2
(mk_list_bar(bar), show_bar)
```],
caption: [
BFS algorithm steps
],
) <standardml-bfs-steps>
In the example above, we see that BFS and propagating constraints to other subgoals can help us cut some search branches to speed up the search.
However, this is not always the case.
BFS is faster only if we manage to cut the proof before exhausting the search for the current goal.
In case the first goal we focus on cannot be filled, DFS is faster as it doesn't do any work on filling other goals.
=== Term search in Haskell
Wingman#cite-footnote("Hackage, Wingman plugin for Haskell Language Server", "2024-04-06", "https://hackage.haskell.org/package/hls-tactics-plugin", "https://web.archive.org/web/20240313211704/https://hackage.haskell.org/package/hls-tactics-plugin") is a plugin for Haskell Language Server that provides term search.
For term search, Wingman uses a library called Refinery#cite-footnote("Github Refinery repository", "2024-04-06", "https://github.com/TOTBWF/refinery", "https://web.archive.org/web/20230615122227/https://github.com/TOTBWF/refinery") that is also based on @algebraic-foundations-of-proof-refinement similarly to the Standard ML tool we described in @standardml.
As we described the core ideas in @standardml, we won't cover them here.
However, we will take a look at some implementation details.
The most interesting implementation detail for us is how BFS is achieved.
Refinery uses the interleaving of subgoals generated by each tactic to get the desired effect.
Let's look at the example to get a better idea of what is going on.
Suppose that at some point in the term search, we have three pending subgoals: `[`#text(red)[`?1`]`, ?2, ?3]` and we have some tactic that produces two new subgoals `[`#text(blue)[`?4`]`, `#text(blue)[`?5`]`]` when refining #text(red)[`?1`].
The DFS way of handling it would be
#block()[
`[`#text(red)[`?1`]`, ?2, ?3] -> tactic -> [`#text(blue)[`?4`]`, `#text(blue)[`?5`]`, ?2, ?3]`
]
However, with interleaving, the goals are ordered in the following way:
#block()[
`[`#text(red)[`?1`]`, ?2, ?3] -> tactic -> [?2, `#text(blue)[`?4`]`, ?3, `#text(blue)[`?5`]`]`
]
Note that there is also a way to insert the new goals at the back of the goals list, which is the BFS way.
#block()[
`[`#text(red)[`?1`]`, ?2, ?3] -> tactic -> [?2, ?3, `#text(blue)[`?4`]`, `#text(blue)[`?5`]`]`
]
However, in Refinery, they have decided to go with interleaving, as it works well with tactics that produce infinite amounts of new holes due to not making any new process.
Note that this works especially well because of the lazy evaluation in Haskell.
In the case of eager evaluation, the execution would still halt, producing all the subgoals, so interlining would now have an effect.
=== Term search in Idris2
Idris2 @idris2-design-and-implementation is a dependently typed programming language that has term search built into its compiler.
Internally, the compiler makes use of a small language they call TT.
TT is a dependently typed λ-calculus with inductive families and pattern-matching definitions.
The language is kept as small as reasonably possible to make working with it easier.
As the term search algorithm also works on TT, we will take a closer look at it.
More precisely, we will look at what they call $"TT"_"dev"$, which is TT extended with hole and guess bindings.
The guess binding is similar to a let binding but without any reduction rules for guess bindings.
Using binders to represent holes is useful in a dependently typed setting since one value may determine another.
Attaching a guess (a generated term) to a binder ensures that instantiating one such variable also instantiates all of its dependencies.
$"TT"_"dev"$ consists of terms, bindings and constants as shown in @idris-tt-syntax.
#figure(
sourcecode(numbering: none)[```
Terms, t ::= c (constant)
| x (variable)
| b. t (binding)
| t t (application)
| T (type constructor)
| D (data constructor)
Binders, b ::= λ x : t (abstraction)
| let x -> t : t (let binding)
| ∀x : t (function space)
| ?x : t (hole binding)
| ?x ≈ t : t (guess)
Constants, c ::= Type (type universes)
| i (integer literal)
| str (string literal)
```],
caption: [
$"TT"_"dev"$ syntax, following @idris2-design-and-implementation[Fig. 1 & Fig. 6] / © Cambridge University Press 2013
],
) <idris-tt-syntax>
Idris2 makes use of a priority queue of holes and guess binders to keep track of subgoals to fill.
The goal is considered filled once the queue becomes empty.
In the implementation, the proof state is captured in an elaboration monad, which is a state monad with exceptions.
The general flow of the algorithm is the following:
1. Create a new proof state.
2. Run a series of tactics to build up the term.
3. Recheck the generated term.
The proof state contains the context of the problem (local and global bindings), the proof term, unsolved unification problems, and the holes queue.
The main parts of the state that change during the proof search are the holes queue and sometimes the unsolved unification problems.
The holes queue changes as we try to empty it by filling all the holes.
Unsolved unification problems only change if new information about unification becomes available when instantiating terms in the proof search.
For example, we may have a unification problem `Unify(f x, Int)` that cannot be solved without new information.
Only when we provide some concrete `f` or `x` the problem can be solved further.
Tactics in Idris2 operate on the sub-goal given by the hole at the head of the hole queue in the proof state.
All tactics run relative to context, which contains all the bindings in scope.
They take a term (that is, hole or guess binding) and produce a new term that is of suitable type.
Tactics are also allowed to have side effects that modify the proof state.
Next, let's take a look at the primitive building blocks that are used by tactics to create and fill holes.
Operation `claim` is used to create new holes in the context of a current hole.
The operation creates a new hole binding to the head of the hole queue.
Note that the binding is what associates the generated hole with the current hole.
Operation `fill` is used to fill a goal with value.
Given the value `v`, the operation attempts to solve the hole by creating a guess binder with `v`.
It also tries to fulfill other goals by attempting to unify `v` with the types of holes.
Note that the `fill` operation does not destroy the hole yet, as the guess binding it created is allowed to have more holes in it.
To destroy holes, the operation `solve` is used.
It operates on guess bindings and checks if they contain any more holes.
If they don't, then the hole is destroyed and substituted with the value from the guess binder.
The two-step process, with `fill` followed by `solve`, allows the elaborator to work safely with incomplete terms.
This way, incomplete terms do not affect other holes (by adding extra constraints) until we know we can solve them.
Once a term is complete in a guess binding, it may be substituted into the scope of the binding safely.
In each of these tactics, if any step fails, or the term in focus does not solve the problem, the entire tactic fails.
This means that it roughly follows the DFS approach described in @standardml.
#pagebreak()
=== Term search in Elm with Smyth
Smyth#cite-footnote("Smyth", "2024-04-06", "https://uchicago-pl.github.io/smyth/", "https://web.archive.org/web/20231005015038/https://uchicago-pl.github.io/smyth/") is a system for program sketching in a typed functional language, approximately Elm.
In @smyth, they describe that it uses evaluation of ordinary assertions that give rise to input-output examples, which are then used to guide the search to complete the holes.
Symth uses type- and example-directed synthesis as opposed to other tools in Agda only using type-guided search for terms.
The general idea is to search for terms that satisfy the goal type as well as example outputs for the term given in assertions.
It is also based on a DFS but is optimized for maximal use memoization.
The idea is to maximize the number of terms that have the same typing environment and can therefore be reused.
This is done by factorizing the terms into smaller terms that carry less context with them.
Smyth has many other optimizations, but they focus on using the information from examples and are therefore not interesting for us as they focus on optimizing the handling of data provided by examples.
== Program synthesis in Rust
RusSol is a proof-of-concept tool to synthesize Rust programs from both function declarations and pre- and post-conditions.
It is based on separation logic as described in @rust-program-synthesis, and it is the first synthesizer for Rust code from functional correctness specifications.
Internally, it uses SuSLik’s @suslik general-purpose proof search framework.
RusSol itself is implemented as an extension to `rustc`, the official rust compiler.
It has a separate command-line tool, but internally, it reuses many parts of the compiler.
Although the main use case for RusSol is quite different from our use case, they share a lot of common ground.
The idea of the tool is to specify the function declaration as follows and then run the tool on it to synthesize the program to replace the ```rust todo!()``` macro on line 5 in @russol-input.
#figure(
sourcecode(highlighted: (5,))[```rs
#[requires(x < 100)]
#[ensures(y && result == Option::Some(x))]
#[ensures(!y && result == Option::None)]
fn foo(x: &i32, y: bool) -> Option<i32> {
todo!()
}
```],
caption: [
RusSol input program
],
) <russol-input>
From the preconditions (`requires` macro) and post-conditions (`ensures` macro), it can synthesize the body of the function.
For the example in @russol-input, the output is shown in @russol-output.
#figure(
sourcecode(numbering: none)[```rs
match y {
true => Some(x),
false => None
}
```],
caption: [
RusSol output for `todo!()` macro
],
) <russol-output>
It can also insert ```rust unreachable!()``` macros in places that are never reached during program execution.
RusSol works at the HIR level of abstraction.
It translates the information from HIR to separation logic rules that SuSLik can understand and feeds them into it.
After getting a successful response, it turns the response back into Rust code, as shown in @russol-workflow.
#figure(
image("fig/russol-suslik.png", width: 100%),
caption: [
"RusSol workflow" by @rust-program-synthesis / #link("https://creativecommons.org/licenses/by/4.0/ ")[CC BY 4.0]
],
) <russol-workflow>
All the programs synthesized by RusSol are guaranteed to be correct by construction.
This is achieved by extracting the programs from separation logic derivations.
However, in @rust-program-synthesis, they noted that they cannot prove the correctness of separation logic rules for Rust as, at this point, Rust lacks formal specification.
Nevertheless, the tool was tested on 100 different crates and managed to always produce a valid code.
As the tool uses an external engine to synthesize the programs, we will not dive into its inner workings.
However, we will take a look at the notes by the authors of @rust-program-synthesis, as they are very relevant to us.
The authors found that quite often the types are descriptive enough to produce useful programs, and the preconditions and postconditions are not required.
This aligns with our intuition that synthesizing terms from types can be useful in practice.
The authors of RusSol pointed out the main limitations of the tool, which are:
1. It does not support traits.
2. It does not support conditionals as it lacks branch abduction.
3. It does not synthesize arithmetic expressions.
4. It does not support ```rust unsafe``` code.
They also noted that the first three of them can be solved with some extra engineering effort, but the last one requires more fundamental changes to the tool.
From the benchmarks on the top 100 crates on crates.io, it was measured that it takes about 0.5s on average to synthesize non-primitive expressions.
Quite often, the synthesis time was 2-3s and sometimes reached as high as 18.3s.
This is fast enough to use for filling holes, but too slow to use for autocompletion.
== Autocompletion
Autocompletion is predicting what the user is typing and then suggesting the predictions to the user.
In the case of programming the suggestions are usually derived from context and may be just a word from the current buffer or maybe functions reachable in the current context.
It is nowadays considered one of the basic features that any integrated development environment (IDE) has built-in.
We will explore the LSP protocol in @lsp-protocol to have a basic understanding of the constraints and features of the framework we are working in.
This is essential to later understand some of our design choices for implementation, as described in @design.
Let's take a look at some of the popular autocompletion tools and their autocompletion-related features to get some intuition of what the common approach is for implementing them.
We will be mostly looking at the kind of semantic information the tools used to provide suggestions.
==== Clangd
Clangd#cite-footnote("Clangd, what is clangd?", "2024-04-06", "https://clangd.llvm.org/", "https://web.archive.org/web/20240324053051/https://clangd.llvm.org/") is a popular autocompletion tool for C/C++.
It is a language server extension to the Clang compiler and, therefore, can be used in many editors.
It suggests functions, methods, variables, etc. are available in the context, and it can handle some mistyping and abbreviations of some words.
For example, using a snake case instead of a camel case still yields suggestions.
For method calls, it does understand the receiver type and only suggests methods and fields that exist for the type.
However, it does not try to infer the expected type of expression that is being completed and therefore is unable to prioritize methods based on that.
All in all, it serves as a great example of an autocompletion tool that has a semantic understanding of the program but does not provide any functionality beyond the basics.
==== Pyright
Pyright#cite-footnote("GitHub pyright repository", "2024-04-06", "https://github.com/microsoft/pyright", "https://web.archive.org/web/20240403213050/https://github.com/microsoft/pyright") is a popular language server for Python.
It suggests all the items that are available in scope for autocompletion, and it also suggests the methods and fields that are on the receiver type.
While it tries to provide more advanced features than `clangd`, it does not get much further due to Python being a dynamically typed language.
There simply isn't that much information available before running the program.
This seems to be a general limitation of all Python autocompletion tools.
==== Intellij
Intellij#cite-footnote("IntelliJ IDEA", "2024-04-06", "https://www.jetbrains.com/idea/", "https://web.archive.org/web/20240409180113/https://www.jetbrains.com/idea/") is an IDE by JetBrains for Java.
Similarly to all other JetBrains products, it does not use LSP but rather has all the tooling built into the product.
It provides the completion of all the items in scope as well as the methods and fields of receiver type.
They call them "basic completions".
The tool also has an understanding of expected types, so it attempts to order the suggestions based on their types.
This means that suggestions with the expected type appear first in the list.
In addition to "basic completion", they provide "type-matching completions", which are very similar to basic completion but filter out all the results that do not have matching types.
There is also what they call "chain completion", which expands the list to also suggest chained method calls.
Together with filtering out only matching types, it gives similar results to what term search provides.
However, as this is implemented differently, its depth is limited to two, which makes it less useful.
It also doesn't attempt to automatically fill all the arguments, so it works best with functions that take no arguments.
For Java, it is quite useful nonetheless, as there are a lot of getter functions.
In some sense, the depth limit of two (or three together with the receiver type) is mainly a technical limitation, but it is also caused by Java using interfaces in a different way than what Rust does with traits.
Interfaces in Java are meant to hide the internal representation of classes, which in some cases limits what we can provide just based on types.
For example, if we are expected to give something that implements `List`, we cannot prefer `ArrayList` to `LinkedList` just based on types.
More common usage of static dispatch in Rust means that we more often know the concrete type and therefore can also provide more accurate suggestions based on it.
In Java, there is often not enough information to suggest longer chains, as there are likely too many irrelevant suggestions.
==== Rust-analyzer <rust-analyzer>
Rust-analyzer#cite-footnote("rust-analyzer", "2024-04-06", "https://rust-analyzer.github.io/", "https://web.archive.org/web/20240406183402/https://rust-analyzer.github.io/") is an implementation of the Language Server Protocol for the Rust programming language.
It provides features like completion and go-to definition/references, smart refactoring, etc.
This is also the tool we are extending with term search functionality.
Rust-analyzer provides all the "basic completions" that IntelliJ provides and also supports ordering suggestions by type.
However, it does not support method chains, so in that regard, it is less powerful than IntelliJ for Java.
Filtering by type is also not part of it, but as it gathers all the information to do it, it can be implemented rather trivially.
Other than autocompletion, it does have an interesting concept of typed holes.
They are `_` (underscore) characters at expression positions that cause the program to be rejected by the compiler.
Rust-analyzer treats them as holes in the program that are supposed to become terms of the correct type to make the program valid.
Based on that concept, it suggests filling them with variables in scope, which is very similar to what term search does.
However, it only suggests trivial ways of filling holes, so we are looking to improve on it a lot.
=== Language Server Protocol <lsp-protocol>
Implementing autocompletion for every language and for every IDE results in a $O(N * M)$ complexity where N is the number of languages supported and M is the number of IDEs supported.
In other words, one would have to write a tool for every language-IDE pair.
This problem is very similar to the problem of compiler design with N languages and M target architectures.
The problem can be reduced from $O(N*M)$ to $O(N+M)$ by separating the compiler to the front- and backend @compiler-design[Section 1.3].
The idea is that there is a unique front end for every language that lowers the language-specific constructs to an intermediate representation that is a common interface for all of them.
To get machine code out of the intermediate representation, there is also a unique back end for every target architecture.
Similar ideas can also be used in building language tools.
Language server protocol (LSP) has been invented to do exactly that.
The Language Server Protocol#cite-footnote("Language Server Protocol", "2024-04-06", "https://microsoft.github.io/language-server-protocol/", "https://web.archive.org/web/20240406114122/https://microsoft.github.io/language-server-protocol/") (LSP) is an open, JSON-RPC-based#cite-footnote("JSON-RPC 2.0 Specification", "2024-04-06", "https://www.jsonrpc.org/specification", "https://web.archive.org/web/20240409000305/https://www.jsonrpc.org/specification") protocol for use between editors and servers that provide language-specific tools for a programming language.
The protocol takes the position of intermediate representation: frontends are the LSP clients in IDEs, and the backends are LSP servers.
We will refer to LSP clients as just clients and LSP servers as just servers.
As the protocol is standardized, every client knows how to work with any server.
LSP was first introduced to the public in 2016, and now many#cite-footnote("The Language Server Protocol implementations: Tools supporting the LSP", "2024-04-06", "https://microsoft.github.io/language-server-protocol/implementors/tools/", "https://web.archive.org/web/20240226024547/https://microsoft.github.io/language-server-protocol/implementors/tools/") modern IDEs support it.
Some of the common functionalities provided by LSP servers include @editing-support-for-languages-lsp:
- Go to definition/reference
- Hover
- Diagnostics (warnings/errors)
- Autocompletion
- Formatting
- Refactoring routines (extract function, etc.)
- Semantic syntax highlighting
Note that the functionalities are optional, and the language server can choose which to provide.
The high-level communication between client and server is shown in @lsp-data-flow.
The idea is that when the programmer works in the IDE, the client sends all text edits to the server.
The server can then process the updates and send new autocompletion suggestions, syntax highlighting and diagnostics back to the client so that it can update the information in the IDE.
#figure(
image("fig/lsp_data_flow.svg", width: 100%),
caption: [
LSP client notifies the server of changes and user requests.
The server responds by providing different functionalities to the client.
],
) <lsp-data-flow>
The important thing to note here is that the client starts the server the first time it requires data from it.
After that, the server runs as a daemon process, usually until the editor is closed or until the client commands it to shut down.
As it doesn't get restarted very often, it can keep the state in memory, which allows responding to client events faster.
It is quite common that the server does semantic analysis fully only once and later only runs the analysis again for files that have changed.
Caching the state and incrementally updating it is quite important, as the full analysis can take up to a considerable amount of time, which is not an acceptable latency for autocompletion nor for other operations servers provide.
Caching the abstract syntax tree is a common performance optimization strategy for servers @editing-support-for-languages-lsp.
== Autocompletion using machine learning <machine-learning>
In this chapter, we will take a look at machine-learning-based autocompletion tools.
As this is a very active field of development and we are not competing against it, we will not dive into how well the models perform but rather look at what the models generally do.
The main focus is to see how they differ from the analytical approach we are taking with term search.
One of the use cases for machine learning is to order the suggestions @code-prediction-trees-transformers.
Using a model for ordering the suggestions is especially useful in dynamically typed languages as it is otherwise rather hard to order suggestions.
Although the Rust language has a strong type system, we still suffer from prioritizing different terms that have the same type.
In addition to ordering the analytically created suggestions, machine learning models can be used to generate code itself.
Such models generate code in a variety of programming languages (@pre-trained-llm-code-gen).
The general flow is that first, the user writes the function signature and maybe some human-readable documentation, and then prompts the model to generate the body of the function.
This is very different from ordering suggestions, as the suggested code usually has many tokens, whereas the classical approach is usually limited to one or sometimes very few tokens.
This is also different from what we are doing with the term search: we only try to produce code that contributes towards the parent term of the correct type.
However, language models can also generate code where term search fails.
Let's look at the example for the `ripgrep`#cite-footnote("GitHub ripgrep repository", "2024-04-06", "https://github.com/BurntSushi/ripgrep/blob/6ebebb2aaa9991694aed10b944cf2e8196811e1c/crates/core/flags/hiargs.rs#L584", "https://web.archive.org/web/20240410184204/https://github.com/BurntSushi/ripgrep/blob/6ebebb2aaa9991694aed10b944cf2e8196811e1c/crates/core/flags/hiargs.rs#L584") crate shown in @rust-builder.
#figure(
sourcecode()[```rs
// Inside `printer_json` at `/crates/core/flags/hiargs.rs`
fn printer_json<W: std::io::Write>(&self, wtr: W) -> JSON<W> {
JSONBuilder::new() // () -> JSONBuilder
.pretty(false) // JSONBuilder -> JSONBuilder
.max_matches(self.max_count) // JSONBuilder -> JSONBuilder
.always_begin_end(false) // JSONBuilder -> JSONBuilder
.build(wtr) // JSONBuilder -> JSON
}
```],
caption: [
Builder pattern in Rust.
Setter methods return a value of the receiver type.
],
) <rust-builder>
The type of term only changes on the first and last lines of the function body.
As the lines in the middle do not affect the type of the builder in any way, there is also no way for the term search to generate them.
Machine learning models, however, are not affected by this, as it may be possible to derive those lines from the function documentation, name, or rest of the context.
Although machine learning models can generate more complex code, they also have the downside of having lots of uncertainty in them.
It is very hard, if not impossible, for any human to understand what the outputs are for any given input.
In the context of code generation for autocompletion, this results in unexpected suggestions that may even not compile.
These issues are usually addressed by filtering out syntactically invalid responses or working at the level of an abstract syntax tree, as they did in @code-prediction-trees-transformers.
However, neither of those accounts for type nor borrow checking, which means that invalid programs can still be occasionally suggested.
= Term search design <design>
Before diving into the technical aspects of term search implementation, we will first explore it by giving
examples of its usages in `rust-analyzer`.
We will first take a look at using it for filling "holes" in the program and later dive into using it for autocompletion.
== Filling holes
Filling holes is a common use case for term search, as we have found in @term-search.
Timing constraints for it are not as strict as for autocompletion, yet the user certainly doesn't want to wait for a considerable amount of time.
One example of a hole in the Rust programming language is the ```rust todo!()``` macro.
It is a "hole", as it denotes that there should be a program in the future, but there isn't now.
These holes can be filled using a term search to search for programs that fit in the hole.
All the programs generated by term search are valid, meaning that they compile.
Example usages can be found in @rust-filling-todo:
#figure(
sourcecode()[```rs
fn main() {
let a: i32 = 0; // Suppose we have a variable a in scope
let b: i32 = todo!(); // Term search finds `a`
let c: Option<i32> = todo!(); // Finds `Some(a)`, `Some(b)` and `None`
}
```],
caption: [
Filling `todo!()` holes
],
) <rust-filling-todo>
In addition to `todo!()` macro holes, `rust-analyzer` has a concept of typed holes, as we described in @rust-analyzer.
From a term search perspective, they work in the same way as ```rust todo!()``` macros: term search needs to come up with a term of some type to fill them.
The same example with typed holed instead of ```rust todo!()``` macros can be found in @rust-filling-typed-hole.
#figure(
sourcecode()[```rs
fn main() {
let a: i32 = 0; // Suppose we have a variable a in scope
let b: i32 = _; // Term search finds `a`
let c: Option<i32> = _; // Finds `Some(a)`, `Some(b)` and `None`
}
```],
caption: [
Filling typed holes (`_`)
],
) <rust-filling-typed-hole>
== Term search for autocompletion
In addition to filling holes, term search can be used to give users "smarter" autocompletion suggestions as they are typing.
The general idea is the same as for filling holes.
We start by attempting to infer the expected type at the cursor.
If we manage to infer the type, then we run the term search to get the suggestions, which we can then show to the user.
The main difference between using term search for autocompletion and using it to fill holes is that we have decided to disable borrow checking when generating suggestions for autocompletion.
This means that not all the suggestions are valid programs and may need some modifications by the user.
The rationale for it comes from both the technical limitations of the tool and different expectations from the user.
The main technical limitation is that borrow checking happens in the MIR layer of abstraction, and `rust-analyzer` (nor `rustc`) does not support lowering partial (the user is still typing) programs to MIR.
This means that borrow checking is not possible without big modifications to the algorithm.
That, however, is out of the scope of this thesis.
In addition to technical limitations, there is also some motivation from a user perspective for the tool to give suggestions that do not borrow check.
Commonly, the programmer has to restructure the program to satisfy the borrow checker @usability-of-ownership.
The simplest case for it is to either move some lines around in the function or to add ```rust .clone()``` to avoid moving the value.
For example, consider @rust-autocompletion with the cursor at "```rust |```":
#figure(
sourcecode(highlighted: (10,))[```rs
/// A function that takes an argument by value
fn foo(x: String) { todo!() }
/// Another function that takes an argument by value
fn bar(x: String) { todo!() }
fn main() {
let my_string = String::new();
foo(my_string);
bar(my_s|); // cursor here at `|`
}
```],
caption: [
Autocompletion of moved values
],
) <rust-autocompletion>
The user wants to also pass `my_string` to ```rust bar(...)```, but this does not satisfy the borrow checking rules as the value was moved to ```rust foo(...)``` on the previous line.
The simplest fix for it is to change the previous line to ```rust foo(my_string.clone())``` so that the value is not moved.
This, however, can only be done by the programmer, as there are other ways to solve it, for example, by making the functions take the reference instead of the value.
As also described in @usability-of-ownership, a common way to handle borrow checker errors is to write the code first and then fix the errors as they come up.
Inspired by this, we believe that it is better to suggest items that make the program not borrow check than not suggest them at all.
If we only suggest items that borrow check the ```rust bar(my_string)``` function call would be ruled out, as there is no way to call it without modifying the rest of the program.
== Implementation
We have implemented term search as an addition to `rust-analyzer`, the official LSP server for the Rust language.
To have a better understanding of the context we are working in, we will first describe the main operations that happen in `rust-analyzer` to provide autocompletion or code actions (filling holes in our use case).
When the LSP server is started, `rust-analyzer` first indexes the whole project, including its dependencies as well as the standard library.
This is a rather time-consuming operation.
During indexing, `rust-analyzer` lexes and parses all source files and lowers most of them to High-Level Intermediate Representation (HIR).
Lowering to HIR is done to build up a symbol table, which is a table that has knowledge of all symbols (identifiers) in the project.
This includes, but is not limited to, functions, traits, modules, ADTs, etc.
Lowering to HIR is done lazily.
For example, many function bodies are usually not lowered at this stage.
One limitation of the `rust-analyzer` as of now is that it doesn't properly handle lifetimes.
Explicit lifetimes are all mapped to ```rust 'static``` lifetimes, and implicit lifetime bounds are ignored.
This also limits our possibilities to do borrow checking as there simply isn't enough data available in the `rust-analyzer` yet.
With the symbol table built up, `rust-analyzer` is ready to accept client requests.
Now an autocompletion request can be sent.
Upon receiving a request that contains the cursor location in the source code, `rust-analyzer` finds the corresponding syntax node.
If it is in a function body that has not yet been lowered, the lowering is done.
Note that the lowering is always cached so that subsequent calls can be looked up from the table.
With all the lowering done, `rust-analyzer` builds up the context of the autocompletion.
The context contains the location in the abstract syntax tree, all the items in scope, package configuration (e.g. is nightly enabled) etc.
If the expected type of the item under completion can be inferred, it is also available in the context.
From the context different completion providers (functions) suggest possible completions that are all accumulated to a list.
To add the term-search-based autocompletion, we introduce a new provider that takes in a context and produces a list of completion suggestions.
Once the list is complete, it is mapped to the LSP protocol and sent back to the client.
=== Term search <term-search-iters>
The main implementation of term search is done at the HIR level of abstraction, and borrow checking queries are made at the MIR level of abstraction.
The term search entry point can be found in `crates/hir/src/term_search.rs` and is named `term_search`.
The most important inputs to the term search are the scope of the program we are performing the search at and the target type.
To better understand why the main algorithm is based around bidirectional BFS, we will discuss three iterations of the algorithm.
First, we start with an algorithm that quite closely follows the algorithm we described in @agsy.
Then we will see how we managed to achieve better results by using BFS instead of DFS, as suggested in @standardml.
At last, we will see how the algorithm can benefit from bidirectional search.
=== First iteration: DFS <first-iter-dfs>
The first iteration of the algorithm follows the algorithm described in @agsy.
The implementation for it is quite short, as the DFS method seems to naturally follow the DFS, as pointed out in @standardml.
However, since our implementation does not use any caching, it is very slow.
Because of the poor performance, we had to limit the search depth to 2, as a bigger depth caused the algorithm to run for a considerable amount of time.
The performance can be improved by caching some of the found terms, but doing it efficiently is rather hard.
Caching the result means that once we have managed to produce a term of type `T`, we want to store it in a lookup table so that we won't have to search for it again.
Storing the type the first time we find it is rather trivial, but it's not very efficient.
The issue arises from the fact that there are no guarantees that the first term we come up with is the simplest.
Consider the example of producing something of the type ```rust Option<i32>```.
We as humans know that the easiest way to produce a term of that type is to use the ```rust None``` constructor that takes no arguments.
The algorithm, however, might first take the branch of using the ```rust Some(...)``` constructor.
Now we have to also recurse to find something of type ```rust i32```, and potentially iterate again and again if we do not have anything suitable in scope.
Even worse, we might end up not finding anything suitable after fully traversing the tree we got from using the ```rust Some(...)``` constructor.
Now we have to also check the ```rust None``` subtree, which means that we only benefit from the cache if we want to search for ```rust Option<i32>``` again.
This is not a problem if we want to retrieve all possible terms for the target type, however, that is not always what we want to do.
We found that for bigger terms, it is better to produce a term with new holes in it, even when we have solutions for them, just to keep the number of suggestions low.
Consider the following example:
#sourcecode(numbering: none)[```rs
let var: (bool, bool) = todo!();
```]
If we give the user back all possible terms, then the user has to choose between the following options:
#sourcecode(numbering: none)[```rs
(false, false)
(false, true)
(true, false)
(true, true)
```]
However, we can simplify it by only suggesting the use of a tuple constructor with two new holes in it.
#sourcecode(numbering: none)[```rs
(todo!(), todo!())
```]
If there are only a few possibilities to come up with a solution, then showing them all isn't a problem.
However, it is quite common for constructors or functions to take multiple arguments.
As the number of terms increases exponentially relative to the number of arguments a function/constructor takes, the number of suggestions grows very fast.
As a result, quite often, all the results don't even fit on the screen.
In @second-iter-bfs, we will introduce an algorithm to handle this case.
For now, it is sufficient to acknowledge that fully traversing the search space to produce all possible terms is not the desired approach, and there is some motivation to cache the easy work to avoid the hard work, not vice versa.
Branch costs suggested in @mimer can potentially improve this, but the issue remains as this is simply a heuristic.
Another observation from implementing the DFS algorithm is that, while most of the algorithm looked very elegant, the "struct projection" tactic described in @tactic-struct-projection was rather awkward to implement.
The issue arose with the projections having to include all the fields from the parent struct as well as from the child struct.
Including only the child "leaf" fields is very elegant with DFS, but also including the intermediate fields caused some extra boilerplate.
Similar issues arose when we wanted to speed up the algorithm by running some tactics, for example, the "impl method" only on types that we have not yet run it on.
Doing it with DFS is possible, but it doesn't fit the algorithm conveniently.
As there were many issues with optimizing the DFS approach, we decided to not improve it further and turned to a BFS-based algorithm instead.
=== Second iteration: BFS <second-iter-bfs>
The second iteration of our algorithm was based on BFS, as suggested in @algebraic-foundations-of-proof-refinement.
However, it differs from it by searching in the opposite direction.
To not confuse the directions, we use _forward_ when we are constructing terms from what we have (working towards the goal) and _backward_ when we work backward from the goal.
This aligns with the forward and the backward directions in generic path finding, where the forward direction is from source to target and the backward direction is from target to source.
The algorithm in @algebraic-foundations-of-proof-refinement starts from the target type and starts working backward from it toward what we already have.
For example, if we have a function in scope that takes us to the goal, we create new goals for all the arguments of the function, therefore we move backward from the return type towards the arguments.
Our algorithm, however, works in the forward direction, meaning that we start from what we have in scope.
We try to apply all the functions, etc. to then build new types from what we have and hopefully, at some point, arrive at the target type.
In @graph-searching, they argue that taking the forward (bottom-up) approach will yield speedups when the active frontier is a substantial fraction of the total graph.
We believe that this might be the case for term search, as there are many ways to build new types available (functions/constructors/methods).
Going in the forward direction, all the terms we create are well-formed and do not have holes in them.
This means that we do not need problem collections, as there are never multiple subproblems pending that have to all be solved for some term to be well-formed.
As there is a potential speedup and the implementation seems to be easier, we decided to experiment with using the forward approach.
Going in the "forward" direction also makes writing some of the tactics easier.
Consider the example of struct projections.
In the backward direction, we would start with the struct field and then later search if we had the struct available.
This works, but it is rather hard to understand, as we usually write code for projections in the forward direction.
With BFS going in the forward direction, we can just visit all the fields of struct types in every iteration, which roughly follows how we usually write code.
The issue of awkward handling of fields together with their fields also goes away, as we can consider only one level of fields in every iteration.
With multiple iterations, we manage to cover fields of nested structs without needing any boilerplate.
In this iteration, we also introduce the cache to the algorithm.
The idea of the cache is to keep track of types we have reached so that we can query for terms of that type in $O(1)$ time complexity.
Since in practice we also care about terms that unify with the type, we get the complexity of $O(n)$ where $n$ is the number of types in the cache.
This is still a lot faster than traversing the tree, as iterating the entries in the map is a quite cheap operation.
With this kind of graph, we managed to increase the search depth to 3-4, depending on the size of the project.
In the DFS approach without cache, the main limitation was time complexity, but now the limitation is memory complexity.
The issue is producing too many terms for a type.
In @first-iter-dfs, we discussed that there are often too many terms to present to the user.
However, now we find that there are also too many terms to keep in memory due to their exponential growth as the depth increases.
Luckily, the idea of suggesting user terms that have new holes in them also reduces the memory complexity a lot.
To avoid producing too many terms we cache terms using enum shown in @rust-alternative-exprs.
#figure(
sourcecode()[```rs
type Cache = Map<Type, AlternativeExprs>;
enum AlternativeExprs {
/// There are few expressions, so we keep track of them all
Few(Set<Expr>),
/// There are too many expressions to keep track of
Many,
}
```],
caption: [
Cache data structure for the term search algorithm
],
) <rust-alternative-exprs>
The idea is that if there are only a few terms of a given type, we keep them all so that we can provide the full term to the user.
However, if there are too many of them to keep track of, we just remember that we can come up with a term for a given type, but we won't store the terms themselves.
The cases of ```rust Many``` later become the holes in the generated term.
In addition to decreasing memory complexity, this also reduces time complexity a lot.
Now we do not have to construct the terms if we know that there are already many of them.
This can be achieved quite elegantly by using iterators in Rust.
Iterators in Rust are lazy, meaning that they only do work if we consume them.
In our case, consuming the iterator is extending the ```rust AlternativeExprs``` in the cache.
However, if we are already in many cases, we can throw away the iterator without performing any computation.
This speeds up the algorithm a lot, so now we can raise the depth of search to 10+ with it still outperforming the previous algorithms on a timescale.
The algorithm itself is quite simple.
The pseudocode for it can be seen in @rust-bfs-pseudocode.
We start by gathering all the items in scope to `defs`.
These items include local values and constants, as well as all visible functions, constructors, etc.
Next, we initialize the lookup table with the desired _many threshold_ for the alternative expressions shown in @rust-alternative-exprs.
The lookup table owns the cache, the state of the algorithm and some other values for optimizations.
We will discuss the exact functionalities of the lookup table in @lookup-table.
Before entering the main loop, we populate the lookup table by running a tactic called `trivial`.
Essentially, it attempts to fulfill the goal by trying the variables we have in scope.
More information about the `trivial` tactic can be found at @tactic-trivial.
All the terms it produces get added to the lookup table and can be later used in other tactics.
After that, we iteratively expand the search space by attempting different tactics until we have exceeded the preconfigured search depth.
During every iteration, we sequentially attempt different tactics.
All tactics build new types from existing types (constructors, functions, methods, etc.) and are described in @tactics.
The search space is expanded by adding new types to the lookup table.
An example of it can be seen in @term-search-state-expansion.
We keep iterating after finding the first match, as there may be many terms of the given type.
Otherwise, we would never get suggestions for ```rust Option::Some(..)```, as ```rust Option::None``` usually comes first as it has fewer arguments.
In the end, we filter out solutions that do not take us closer to the goal.
#figure(
sourcecode()[```rs
pub fn term_search(ctx: &TermSearchCtx) -> Vec<Expr> {
let mut defs = ctx.scope.process_all_names(...);
let mut lookup = LookupTable::new(ctx.many_threshold);
// Try trivial tactic first, also populates lookup table
let mut solutions: HashSet<Expr> =
tactics::trivial(ctx, &defs, &mut lookup).collect();
for _ in 0..ctx.config.depth {
lookup.new_round();
solutions.extend(tactics::type_constructor(ctx, &defs, &mut lookup));
solutions.extend(tactics::free_function(ctx, &defs, &mut lookup));
solutions.extend(tactics::impl_method(ctx, &defs, &mut lookup));
solutions.extend(tactics::struct_projection(ctx, &defs, &mut lookup));
solutions.extend(tactics::impl_static_method(ctx, &defs, &mut lookup));
}
solutions.into_iter().filter(|it| !it.is_many()).collect()
}
```],
caption: [
Forward direction term search pseudocode
],
) <rust-bfs-pseudocode>
As we can see from the @rust-bfs-pseudocode, we start with what we have (locals, constants, and statics) and work towards the target type.
This is in the opposite direction compared to the tools we have looked at previously.
To better understand how the search space is expanded, let us look at @term-search-state-expansion.
#figure(
image("fig/state_expansion.svg", width: 60%),
caption: [
Iterative term search state expansion.
We start with terms of types A and B.
With every iteration, we keep the terms from the previous iteration and add new terms if possible.
],
) <term-search-state-expansion>
We start with variables `a` of type `A` and `b` of type `B`.
In the first iteration, we can use the function $f: A -> C$ on `a` and get something of the type `C`.
in the iteration after that, we can use $g: C times B -> D$ and produce something of type `D`.
Once we have reached the maximum depth, we take all the elements that unify with the goal type and return all paths that take us to the goal type.
==== Lookup table <lookup-table>
The main task of the lookup table throughout the algorithm is to keep track of the state.
The state consists of the following components:
1. _Terms reached_ (grouped by type)
2. _New types reached_ (since last iteration)
3. _Definitions used_ and _definitions exhausted_ (for example, functions applied)
4. _Types wishlist_ (types that have been queried, but not reached)
_Terms reached_ keeps track of the search space we have already covered (visited types) and allows querying terms in $O(1)$ complexity for exact type and $O(n)$ complexity for types that unify.
It is important to note that it also performs the transformation of taking a reference if we query for a reference type.
This is only to keep the implementation simple and the memory footprint low.
Otherwise, having a separate tactic for taking a reference of this type would be preferred.
_New types reached_ keeps track of new types added to _terms reached_ so that we can iterate only over them in some tactics to speed up the execution.
_Definitions used_ serves also only the purpose of speeding up the algorithm by avoiding definitions that have already been used.
_Types wishlist_ keeps track of all the types we have tried to look up from terms reached but not found.
They are used in the static method tactic (see @tactic-static-method) to only search for static methods on types we haven't reached yet.
This is another optimization for speed described in the @tactic-static-method.
The main downside of the lookup table implementation we have is that it poorly handles types that take generics.
We only store types that are normalized, meaning that we have substituted the generic parameter with some concrete type.
In the case of generics, it often means that the lookup table starts growing exponentially.
Consider the example of using the `Option` type.
#sourcecode()[```rs
Some(T) | None
Some(Some(T)) | Some(None) | Some(T) | None
Some(Some(Some(T))) | Some(Some(None)) | Some(Some(T)) | Some(None) | Some(T) | None
```]
With every iteration, two new terms of a new type become available, even though it is unlikely one would ever use them.
However, since `Option` takes only one generic argument, the growth is linear as many of the terms cancel out due to already being in the cache.
If we have something with multiple generic parameters, it becomes exponential.
Consider the example of wrapping the types we have to pair (a tuple with two elements).
At first, we have $n$ types.
After the first iteration, we have $n^2$ new types as we are taking the Cartesian product.
In the second iteration, we can create a pair by taking one of the elements from the original set of types and the second element from the set of pairs we have.
As for every pair, there are $n$ original types to choose from and we get $n^3$ pairs and also all the pairs of pairs.
Even without considering the pairs of pairs, we see that the growth is exponential.
To keep the search space to a reasonable size, we ignore all types with generics unless they are directly related to the goal.
This means that we limit the depth for the generics to 1, which is a very severe but necessary limitation.
In @third-iter-bidirectional-bfs, we will discuss how to get around this limitation.
=== Third iteration: Bidirectional BFS <third-iter-bidirectional-bfs>
The third iteration of our algorithm is a small yet powerful improvement on the second iteration described in @second-iter-bfs.
This iteration differs from the previous one by improving the handling of generics.
We note that the handling of generics is a much smaller problem if going in the backward direction similar to other term search tools.
This is because we can only construct the types that contribute towards reaching the goal.
However, if we only go in the backward direction, we can still end up with terms such as ```rust Some(Some(...)).is_some()``` that do contribute towards the goal but not in a very meaningful way.
BFS copes with these kinds of terms quite well, as the easiest paths are taken first.
However, with multiple iterations, many not-so-useful types get added to the lookup table nonetheless.
Note that the trick with lazy evaluation of iterators does not work here as the terms have types not yet in the lookup, meaning we cannot discard them.
Filtering them out in a backward direction is possible but not trivial.
To benefit from better handling of generics going in the backward direction and an otherwise more intuitive approach of going in the forward direction, we decided to make the search bidirectional.
The forward direction starts with the locals we have and starts expanding the search space from there.
Tactics that work in the forward direction ignore all types where we need to provide generic parameters.
Other tactics start working backward from the goal.
All the tactics that work backward do so to better handle generics.
Going backward is achieved by using the types wishlist component of the lookup table.
We first seed the wishlist with the target type.
During every iteration, the tactics working backward from the target type only work with the concrete types we have in our wishlist.
For example, if there is ```rust Option<Foo>``` in the wishlist and we work with the ```rust Option<T>``` type, we know to substitute the generic type parameter `T` with ```rust Foo```.
This way, we avoid polluting the lookup table with many types that likely do not contribute towards the goal.
All the tactics add types to the wishlist, so forward tactics can benefit from the backward tactics (and vice versa) before meeting in the middle.
With some tactics, such as using methods on types only working in the forward direction, we can conveniently avoid adding complex types to the wishlist if we only need them to get something simple, such as ```rust bool``` in the ```rust Some(Some(...)).is_some()``` example.
== Tactics <tactics>
We use tactics to expand the search space for the term search algorithm.
All the tactics are applied sequentially, which causes a phase-ordering problem as tactics generally depend on the results of others.
However, the ordering of tactics problem can be fixed by running the algorithm for more iterations.
Note that some tactics also use heuristics for performance optimization that also suffer from the phase ordering problem, but they cannot be fixed by running the algorithm for more iterations.
All the tactic function signatures follow the simplified function signature shown in @rust-tactic-signature.
#figure(
sourcecode(numbering: none)[
```rs
fn tactic_name(
ctx: &TermSearchCtx,
defs: &HashSet<ScopeDef>,
lookup: &mut LookupTable,
) -> impl Iterator<Item = Expr>
```],
caption: [
Term search tactic signature.
Arguments `ctx` and `defs` give all the available context.
State is encapsulated in `lookup`.
All tactics return an iterator that yields terms that unify with the goal.
],
) <rust-tactic-signature>
All the tactics take in the context of term search, definitions in scope, and a lookup table and produce an iterator that yields expressions that unify with the goal type (provided by the context).
The context encapsulates the semantics of the program, the configuration for the term search, and the goal type.
Definitions are all the definitions in scope that can be used by tactics.
Some examples of definitions are local variables, functions, constants, and macros.
The definitions in scope can also be derived from the context, but they are kept track of separately to speed up the execution by filtering out definitions that have already been used.
Keeping track of them separately also allows querying them only once, as they do not change throughout the execution of the algorithm.
The lookup table is used to keep track of the state of the term search, as described in @lookup-table.
The iterator produced by tactics is allowed to have duplicates, as filtering of them is done at the end of the algorithm.
We decided to filter at the end because it is hard to guarantee that different tactics do not produce the same elements, but without the guarantee of uniqueness, there would have to be another round of deduplication nevertheless.
==== Tactic "trivial" <tactic-trivial>
A tactic called "trivial" is one of the most trivial tactics we have.
It only attempts items we have in scope and does not consider any functions/constructors.
The items in scope contain:
1. Constants
2. Static items
3. Generic parameters (constant generics#cite-footnote("The Rust Reference, Generic parameters", "2024-04-06", "https://doc.rust-lang.org/reference/items/generics.html", "https://web.archive.org/web/20240324062312/https://doc.rust-lang.org/reference/items/generics.html"))
4. Local items
As this tactic only depends on the values in scope, we don't have to call it every iteration.
We only call it once before any of the other tactics to populate the lookup table for forward direction tactics with the values in scope.
/*
$
(x_"constant": A in Gamma #h(0.5cm) ?: A) / (? := x_"constant")
#h(1cm)
(x_"static": A in Gamma #h(0.5cm) ?: A) / (? := x_"static") \
\
(x_"generic": A in Gamma #h(0.5cm) ?: A) / (? := x_"generic")
#h(1cm)
(x_"local": A in Gamma #h(0.5cm) ?: A) / (? := x_"local")
$
*/
==== Tactic "famous types" <tactic-famous-types>
"Famous types" is another rather trivial tactic.
The idea of the tactic is to attempt values of well-known types.
Those types and values are:
1. ```rust true``` and ```rust false``` of type ```rust bool```
2. ```rust ()``` of unit type ```rust ()```
While we usually try to avoid creating values out of the blue, we make an exception here.
The rationale for making the types we generate depend on the types we have in scope is that usually, the programmer writes the code that depends on inputs or previous values.
Suggesting something else can be considered distracting.
However, we find these values to be common enough to usually be a good suggestion.
Another reason is that we experienced our algorithm "cheating" around depending on values anyway.
It constructed expressions like ```rust None.is_none()``` and ```rust None.is_some()``` for ```rust true```/```rust false``` which are valid but most likely never what the user wants.
For unit types, it can use any function that has "no return type", meaning it returns a unit type.
There is usually at least one that kind of function in scope, but suggesting it is unexpected more often than suggesting `()`.
Moreover, suggesting a random function with a `()` return type can often be wrong as the functions can have side effects.
Similarly to the tactic "trivial", this tactic helps to populate the lookup table for the forward pass tactics.
/*
$
(?: "bool") / (? := "true" #h(0.5cm) ? := "false")
#h(1cm)
(?: "()") / (? := "()")
$
*/
==== Tactic "data constructor"
"Data constructor" is the first of our tactics that takes us from terms of some types to terms of other types.
The idea is to attempt to apply the data constructors of the types we have in scope.
We try them by looking for terms for each of the arguments the constructor has from the lookup table.
If we have terms for all the arguments, then we have successfully applied the constructor.
If not, then we cannot apply the constructor at this iteration of the algorithm.
The tactic includes both sum and product types (`enum` and `struct` for Rust).
As compound types may contain generic arguments, the tactic works in both forward and backward directions.
The forward direction is used if the ADT does not have any generic parameters.
The backward direction is used for types that have generic parameters.
In the backward direction, all the generic type arguments are taken from the types in the wishlist.
By doing that, we know that we only produce types that somehow contribute to our search.
The tactic avoids types that have unstable generic parameters that do not have default values.
Unstable generics with default values are allowed, as many of the well-known types have unstable generic parameters that have default values.
For example, the definition for ```rust Vec``` type in Rust is the following:
```rs
struct Vec<T, #[unstable] A: Allocator = Global>
```
As the users normally avoid providing generic arguments that have default values, we also decided to avoid filling them.
This means that for the ```rust Vec``` type above, the algorithm only tries different types for `T` but never touches the `A` (allocator) generic argument.
/*
$
T_"struct" = A times B times A times C #h(1cm) T_"enum" = A + B + C\
\
(a: A, b: B, c: C in Gamma #h(0.5cm) ?: T_"struct") /
(? := T_"struct" (a,b,a,c)) \
\
(a: A in Gamma #h(0.5cm) ?: T_"enum") /
(? := T_"enum" (a))
#h(1cm)
(b: B in Gamma #h(0.5cm) ?: T_"enum") /
(? := T_"enum" (b))
#h(1cm)
(c: C in Gamma #h(0.5cm) ?: T_"enum") /
(? := T_"enum" (c))
$
*/
==== Tactic "free function"
This tactic attempts to apply free functions we have in scope.
It only tries functions that are not part of any ```rust impl``` block (associated with type or trait) and are therefore considered "free".
A function can be successfully applied if we have terms in the lookup table for all the arguments that the function takes.
If we are missing terms for some arguments, we cannot use the function, and we try again in the next iteration when we hopefully have more terms in the lookup table.
We have decided to filter out all the functions that have non-default generic parameters.
This is because `rust-analyzer` does not have proper checking for the function to be well-formed with a set of generic parameters.
This is an issue if the generic parameters that the function takes are not present in the return type.
As we ignore all the functions that have non-default generic parameters we can run this tactic in only the forward direction.
The tactic avoids functions that return types that contain references (@tactics).
However, we do allow function arguments to take items by shared references as this is a common practice to pass by reference rather than value.
/*
$
(a: A, b: B in Gamma #h(0.5cm) f: A times B -> C in Gamma #h(0.5cm) ?: C) /
(? := f(a, b)) \
$
*/
==== Tactic "impl method"
This tactic attempts functions that take a ```rust self``` parameter.
This includes both trait methods and methods implemented directly on type.
Examples for both of these cases are shown in @rust-impl-method.
Both of the impl blocks are highlighted, and each of them has a single method that takes a ```rust self``` parameter.
These methods can be called as ```rust example.get_number()``` and ```rust example.do_thingy()```.
#figure(
sourcecode(highlighted: (5,6,7,8,9, 15,16,17,18,19))[```rs
struct Example {
number: i32,
}
impl Example {
fn get_number(&self) -> i32 {
self.number
}
}
trait Thingy {
fn do_thingy(&self);
}
impl Thingy for Example {
fn do_thingy(&self) {
println!("doing a thing! also, number is {}!", self.number);
}
}
```],
caption: [
Examples of ```rust impl``` blocks, highlighted in yellow
],
) <rust-impl-method>
Similarly to the "free function" tactic, it also ignores functions that have non-default generic parameters defined on the function for the same reasons.
However, generics defined on the ```rust impl``` block pose no issues as they are associated with the target type, and we can provide concrete values for them.
A performance tweak for this tactic is to only search the ```rust impl``` blocks for types that are new to us, meaning that they were not present in the last iteration.
This implies we run this tactic only in the forward direction, i.e. we need to have a term for the receiver type before using this tactic.
This is a heuristic that speeds up the algorithm quite a bit, as searching for all ```rust impl``` blocks is a costly operation.
However, this optimization does suffer from the phase ordering problem.
For example, we may want to use use some method from the ```rust impl``` block later, when we have reached more types and covered a type that we need for an argument of the function.
We considered also running this tactic in the reverse direction, but it turned out to be very hard to do efficiently.
The main issue is that there are many ```rust impl``` blocks for generic `T` that do not work well with the types wishlist we have, as it pretty much says that all types belong to the wishlist.
One example of this is shown in @rust-blanket-impl.
#figure(
sourcecode(numbering: none)[```rs
impl<T: fmt::Display + ?Sized> ToString for T {
fn to_string(&self) -> String { /* ... */ }
}
```],
caption: [
Blanket ```rust impl``` block for ```rust ToString``` trait in the standard library.
All the types that implement ```rust fmt::Display``` also implement ```rust ToString```.
],
) <rust-blanket-impl>
One interesting aspect of Rust to note here is that even though we can query the ```rust impl``` blocks for type, we still have to check that the receiver argument is of the same type.
This is because Rust allows also some other types that dereference to the type of ```rust Self``` for the receiver argument#cite-footnote("The Rust Reference, Associated Items", "2024-04-06", "https://doc.rust-lang.org/reference/items/associated-items.html#methods", "https://web.archive.org/web/20240324062328/https://doc.rust-lang.org/reference/items/associated-items.html#methods").
These types include but are not limited to ```rust Box<S>```, ```rust Rc<S>```, ```rust Arc<S>```, and ```rust Pin<S>```.
For example, there is a method signature for the ```rust Option<T>``` type in the standard library#cite-footnote("Rust standard library source code", "2024-04-06", "https://doc.rust-lang.org/src/core/option.rs.html#715", "https://web.archive.org/web/20240317121015/https://doc.rust-lang.org/src/core/option.rs.html#715") shown in @rust-receiver-type.
#figure(
sourcecode(numbering: none)[```rs
impl<T> Option<T> {
pub fn as_pin_ref(self: Pin<&Self>) -> Option<Pin<&T>> { /* ... */ }
}
```],
caption: [
Receiver argument with type other than ```rust Self```
],
) <rust-receiver-type>
As we can see from the snippet above, the type of ```rust Self``` in the ```rust impl``` block is ```rust Option<T>```.
However, the type of ```rust self``` parameter in the method is ```rust Pin<&Self>```, which means that to call the `as_pin_ref` method, we need to have an expression of type ```rust Pin<&Self>```.
We have also decided to ignore all the methods that return the same type as the type of ```rust self``` parameter.
This is because they do not take us any closer to the goal type, and we have considered it unhelpful to show users all the possible options.
If we allowed them, then we would also receive expressions such as ```rust some_i32.reverse_bits().reverse_bits().reverse_bits()``` which is valid Rust code but unlikely something the user wished for.
Similar issues often arise when using the builder pattern, as shown in @rust-builder.
/*
#todo("same as free function as the self is not really that special")
$
(a: A, b: B in Gamma #h(0.5cm) f: A times B -> C in Gamma #h(0.5cm) ?: C) /
(? := f(a, b)) \
$
*/
==== Tactic "struct projection" <tactic-struct-projection>
"Struct projection" is a simple tactic that attempts all field accesses of struct.
The tactic runs only in the forward direction, meaning we only try to access fields of the target type rather than search for structs that have fields of the target type.
In a single iteration, it only goes one level deep, but with multiple iterations, we cover all the fields of substructs.
This tactic greatly benefits from the use of BFS over DFS, as the implementation for accessing all the fields of the parent struct is rather trivial, and with multiple iterations, we get the full coverage, including substruct fields.
With DFS, the implementation was much more cumbersome, as simple recurring on all the fields leaves out the fields themselves.
As a result, the implementation for DFS was about two times longer than the implementation for BFS.
As a performance optimization, we only run this tactic on every type once.
For this tactic, this optimization does not reduce the total search space covered, as accessing the fields doesn't depend on the rest of the search space covered.
/*
#todo("Should we show all fields and how to name them?")
$
T_"struct" = A times B times A times C\
\
(s: T_"struct" in Gamma #h(0.5cm) ?: A) /
(? := s.a) \
$
*/
==== Tactic "static method" <tactic-static-method>
The "Static method" tactic attempts static methods of ```rust impl``` blocks, that is, methods that are associated with either type or trait, but do not take the ```rust self``` parameter.
Some examples of static methods are ```rust Vec::new()``` and ```rust Default::default()```.
As a performance optimization, we query the ```rust impl``` block for types we have a wishlist, meaning we only go in the backward direction.
This is because we figured that the most common use case for static methods is the factory method design pattern described in @design-patterns-elements-of-reusable-oo-software.
Querying ```rust impl``` blocks is a costly operation, so we only do it for types that are contributing towards the goal, meaning they are in the wishlist.
Similarly to the "Impl method" tactic, we ignore all the methods that have generic parameters defined at the method level for the same reasoning.
/*
#todo("This is same as free function again...")
$
(a: A, b: B in Gamma #h(0.5cm) f: A times B -> C in Gamma #h(0.5cm) ?: C) /
(? := f(a, b)) \
$
*/
==== Tactic "make tuple"
The "make tuple" tactic attempts to build types by constructing a tuple of other types.
This is another tactic that runs only in the backward direction, as otherwise, the search space would grow exponentially.
In Rust, the issue is even worse as there is no limit to how many items can be in a tuple, meaning that even with only one term in scope, we can create infinitely many tuples by repeating the term an infinite number of times.
Going in the backward direction, we can only construct tuples that are useful and therefore keep the search space reasonably small.
/*
$
(a: A, b: B in Gamma #h(0.5cm) ?: (A, B)) /
(? := (a, b)) \
$
*/
= Evaluation <evaluation>
In this chapter, we evaluate the performance of the three iterations of the algorithm as implemented in @term-search-iters.
The main focus is on the third and final iteration, but we compare it to previous iterations to highlight the differences.
First, we perform an empirical evaluation of the tree algorithms by performing a resynthesis on existing Rust programs.
Later, we focus on some hand-picked examples to show the strengths and weaknesses of the tool.
== Resynthesis
Resynthesis is using the tool to synthesize programs for which a reference implementation exists.
This allows us to compare the generated suggestions to known-good programs.
For resynthesis, proceed as follows:
1. Take an existing open-source project as a reference implementation.
2. Remove one expression from it, creating a hole in the program.
3. Run the term search in the hole.
4. Compare the generated expressions to the reference implementation.
5. Put back the original expression and repeat on the rest of the expressions.
==== Choice of expressions
We chose to perform resynthesis only on the #emph[tail expressions] of blocks, as we consider this the most common use case for our tool.
A block expression is a sequence of statements followed by an optional tail expression, enclosed in braces (`{...}`).
For example, the body of a function is a block expression, and the function evaluates to the value of its tail expression.
Block expressions also appear as the branches of ```rust if``` expressions and ```rust match```-arms.
For some examples, see @rust-tail-expr.
#figure(
sourcecode(highlighted: (4, 10, 13, 17, 21))[
```rs
fn foo(x: Option<i32>) -> Option<bool> {
let y = {
/* Compute something */
true
}
let res = match x {
Some(it) => {
if x < 0 {
/* Do something */
true
} else {
/* Do something else */
false
}
}
None => {
true
}
}
Some(res)
}
```],
caption: [
Examples of tail expressions: in a scoping block (line 4), in branch arms (line 10, 13, 17) and the return position (line 21).
],
) <rust-tail-expr>
==== Choice of metrics
For resynthesis, we are interested in the following metrics:
1. #metric[Holes filled] represents the fraction of tail expressions where the algorithm finds at least one term that satisfies the type system. The term may or may not be what was there originally.
2. #metric[Holes filled (syntactic match)] represents the share of tail expressions relative to the total number of terms that are syntactically equal to what was there before. Note that syntactical equality is a very strict metric, as programs with different syntax may have the same meaning. For example, ```rust Vec::new()``` and ```rust Vec::default()``` produce exactly the same behavior. As deciding the equality of the programs is generally undecidable according to Rice's theorem @rice-theorem, we will not attempt to consider the equality of the programs and settle for syntactic equality.
To make the metric slightly more robust, we compare the program's ASTs, effectively removing all the formatting before comparing.
3. #metric[Average time] represents the average time for a single term search query. Note that although the cache in term search does not persist between runs, the lowering of the program is cached. This is however also true for the average use case of `rust-analyzer` as it only wipes the cache on restart.
To benchmark the implementation of term search rather than the rest of `rust-analyzer` we run term search on hot cache.
4. #metric[Terms per hole] - This shows the average number of options provided to the user.
These metrics are relatively easy to measure and relevant to users:
They tell us how often the tool offers assistance, how much of it is useful, and if it slows down the user's flow of development.
All experiments are conducted on a consumer-grade computer with an AMD Ryzen 7 CPU and 32GB of RAM.
==== Choice of reference implementations
For our experiments, we select a number of open-source Rust libraries.
In Rust, #emph[crate] is the name for a library.
We use _crates.io_#cite-footnote("The Rust community’s crate registry", "2024-04-06", "https://crates.io/", "https://web.archive.org/web/20240409223247/https://crates.io/"), the Rust community’s crate registry as a source of information of the most popular crates.
_Crates.io_ is the _de facto_ standard crate registry, so we believe that it reflects the popularity of the crates in the Rust ecosystem very well.
We select representative examples of different kinds of Rust programs by picking crates from popular categories on _crates.io_.
For each category containing at least 1000 crates, we select its top 5 crates, sorted by all-time downloads.
This leaves us with 31 categories and a total of 155 crates.
The full list of crates can be seen in #ref(<appendix-crates>, supplement: "Appendix").
==== Results
First, we are going to take a look at how the hyperparameter of search depth affects the chosen metrics.
We measured #metric[holes filled] and the number of #metric[terms per hole] for search depths up to 5 (@term-search-depth-accuracy, @tbl-depth-hyper-param).
For search depth 0, only trivial tactics (@tactic-trivial and @tactic-famous-types) are run.
This results in 18.9% of the holes being filled, with only 2.5% of the holes having syntactic matches.
Beyond the search depth of 2, we noticed barely any improvements in the portion of holes filled.
At depth 2, the algorithm fills 74.9% of holes.
By doubling the depth, the number of holes filled increases only by 1.5%pt to 76.4%.
More interestingly, we can see from @tbl-depth-hyper-param that syntactic matches start to decrease after a depth of 3.
This is because we get more results for subterms and squash them into ```rust Many```, i.e. replace them with a new hole.
Terms that would result in syntactic matches get squashed, resulting in a decrease in syntactic matches.
The number of terms per hole follows a similar pattern to holes filled, but the curve is flatter.
At depth 0, we have, on average, 15.1 terms per hole.
At depths above 4, this number plateaus at around 23 terms per hole.
Note that a larger number of terms per hole is not always better.
Too many terms might be overwhelming to the user.
Over 15 terms per hole at depth 0 is more than we expected, so we will more closely investigate the number of terms per hole in @c-style-stuff.
#figure(
placement: auto,
grid(
image("fig/accuracy.png", width: 100%),
image("fig/nr_suggestions.png", width: 100%),
),
caption: [
The effect of search depth on the fraction of holes filled, and the average number of terms per hole.
For depth >2, the number of holes filled plateaus.
Syntactic matches do not improve at depth above 1.
The number of terms per hole starts at a high number of 15 and increases until the depth of 4 reaching 22.
],
) <term-search-depth-accuracy>
To more closely investigate the time complexity of the algorithm, we run the experiment up to a depth of 20.
We estimate that running the experiment on all 155 crates would take about half a month.
To speed up the process, we select only the most popular crate for each category.
This results in 31 crates in total (#ref(<appendix-reduced-crates>, supplement: "Appendix")).
We observe that in the average case, the execution time of the algorithm is in linear relation to the search depth (@term-search-depth-time).
Increasing depth by one adds about 8ms of execution time on average.
#figure(
placement: auto,
image("fig/time.png", width: 90%),
caption: [
The execution time of the algorithm is linear in the search depth.
$"Slope" = 7.6"ms"/"depth"$, standard deviation = 6.7ms
],
) <term-search-depth-time>
We can see that increasing the search depth over two can have somewhat negative effects.
The search will take longer, and there will be more terms.
More terms often mean more irrelevant suggestions.
By examining the fraction of holes filled and holes filled with syntactic matches, we see that both have reached a plateau at depth 2.
From that, we conclude that we are mostly increasing the number of irrelevant suggestions.
This can also be seen in @term-search-depth-accuracy, where the fraction of holes filled has stalled after the second iteration, but execution time keeps increasing linearly in @term-search-depth-time.
#figure(
placement: auto,
table(
columns: 5,
inset: 5pt,
align: horizon,
table.header[*Depth*][*Holes filled*][*Syntactic matches*][*Terms per hole*][*Average time*],
[0], [18.9%], [2.5%], [15.1], [0.5ms],
[1], [68.6%], [11.0%], [18.1], [7.1ms],
[2], [74.9%], [11.3%], [20.0], [49.5ms],
[3], [76.1%], [11.4%], [21.5], [79.5ms],
[4], [76.4%], [11.3%], [22.1], [93.9ms],
[5], [76.5%], [11.3%], [22.3], [110.1ms],
),
caption: [
Depth hyperparameter effect on metrics.
_Holes filled_ plateaus at 76% on depth 2.
_Syntactic matches_ reaches 11.4% at depth 3 and starts decreasing.
_Terms per hole_ starts at a high number of 15 per hole, plateaus at depth 4 around 22 terms per hole.
_Average time_ increases about linearly.
]
) <tbl-depth-hyper-param>
With a depth of 2, the program manages to generate a term that satisfies the type for 74.9% of all holes.
In 11.0% of searches, the generated term syntactically matches the original term.
The average number of terms per hole is 20, and they are found in 49ms.
However, the numbers vary a lot depending on the style of the program.
The standard deviation between categories for the average number of terms is about 56 terms, and the standard deviation of the average time is 135ms.
Both of these are greater than the average numbers themselves, indicating large differences between categories.
We discuss the categories that push the standard deviation so high in @c-style-stuff.
#let ver(x) = raw("v" + str(x))
To give some context to the results, we decided to compare them to results from previous iterations of the algorithm.
However, both of the previous algorithms were so slow with some particular crates that we couldn't run them on the whole set of benchmarks.
As some of the worst cases are eliminated for iterations #ver(1) and #ver(2), the results in @tbl-versions-comparison are more optimistic for #ver(1) and #ver(2) than for the final iteration of the algorithm.
Nevertheless, the final iteration manages to outperform both of the previous iterations.
The first iteration performs significantly worse than others, running almost two orders of magnitude slower than other iterations and filling about only a third of the holes compared to the final iteration of the algorithm.
As the performance of the first iteration is much worse than the later iterations, we will not dive into the details of it.
Instead, we compare the last two iterations more closely.
The final iteration manages to fill 1.6 times more holes than the second iteration of the algorithm at depth 3.
It also fills 1.8 times more holes with syntactic matches.
These results were achieved in 12% less time than the second iteration.
#figure(
// placement: auto,
table(
columns: 5,
align: (x, _) => if x == 4 { right } else { horizon },
inset: 5pt,
table.header[*Algorithm*][*Holes filled*][*Syntactic matches*][*Terms per hole*][*Avg time*],
[#ver(1), $"depth"=1$], [26%], [4%], [5.8], [4900ms],
[#ver(2), $"depth"=3$], [46%], [6%], [17.2], [90ms],
//[v3, $"depth"=2$], [75%], [11%], [20.0], [49ms],
[#ver(3), $"depth"=3$], [76%], [11%], [21.5], [79ms],
),
caption: [
Comparison of algorithm iterations.
#ver(1) performs the worst in every metric, especially execution time.
#ver(2) runs slightly slower than #ver(3), and fills significantly fewer holes.
// V3 with depth 2 outperforms V2 with depth 3 by filling more holes in half the time.
]
) <tbl-versions-comparison>
In addition to average execution time, we care about the low latency of suggestions.
We chose 100ms as a latency threshold, which we believe is low enough for responsive autocompletion.
This is a recommended latency threshold for web applications (@usability-engineering), and the mean latency of writing digraphs while programming is around 170ms (@typing-latency).
We will use our algorithm with a depth of 2, as this seems to be the optimal depth for autocompletion.
We found that 87% of holes can be filled within 100ms.
In 8 of the categories, all holes could be filled in 100ms.
The main issues arose in the categories "hardware-support" and "external-ffi-bindings", in which only 6% and 16% of the holes could be filled within the 100ms threshold.
These categories were also problematic from the other aspects, and we will discuss the issues in them in detail in @c-style-stuff.
== Usability <usability>
In this section, we study cases where our algorithm either performs very well or very poorly.
We discuss the performance of our algorithm for different styles of programs as well as in different contexts in which to perform term searches.
==== Generics
Although we managed to make the algorithm work decently with a low amount of generics, extensive use of generics slows it down.
Crates in the category "mathematics" are highly generic, and as a result, the average search time in this category is about 15 times longer than the average overall categories (767ms vs 50ms, @tbl-per-category-results).
One example is `nalgebra`#cite-footnote("Crates.io, nalgebra library", "2024-04-06", "https://crates.io/crates/nalgebra", "https://web.archive.org/web/20230928073209/https://crates.io/crates/nalgebra") crate,
which uses generic parameters in almost all of its functions.
The slowdown occurs because the wishlist of types grows very large since there are many generic types with different trait bounds.
==== Tail expressions
We find that tail expressions are one of the best contexts to perform term searches.
They are a good fit for both filling holes and also for providing autocompletion suggestions, for the following reasons:
1. Tail expressions usually have a known type.
The type is either written explicitly (e.g. a function return type) or can be inferred from context (e.g. all match arms need to have the same type).
2. Once the user starts writing the tail expression, they usually have enough terms available in context to fill the hole.
For example, it is common to store `struct` fields in local variables and then combine them into a `struct` only in the tail expression.
Accurate type information is essential for the term search to provide good suggestions.
When filling holes, the user has often already put in some extra effort by narrowing down the type of hole.
Non-tail expressions, however, often lack enough type information, and thus autocompletion produces no suggestions at all.
==== Function arguments
We found that letting the algorithm search for parameters of a function call yields good results.
This is especially true when the user is working in "exploration mode" and is looking to find different ways of calling the function.
Similarly to tail expressions, function calls usually have accurate type information available for the arguments, with some exceptions for generic types.
Often, there are also arguments of the right type available in context, so the term search can easily fill them in.
==== Local variables
In practice, term search is not very useful for generating terms for local variables.
Usually, a local variable is bound in a `let`-statement, and it is common to omit its type and let the compiler infer it instead.
This, however, means that there is no type information available for the term search.
Adding the type explicitly fixes the issue, but this results in non-idiomatic Rust code.
In this regard, type inference and term search have opposite goals:
One finds types for programs, and the other finds programs for types.
==== Builder pattern
As discussed in @machine-learning, term search struggles to suggest terms of types using the builder pattern.
Suggestions like `Foo::builder().build()` are incomplete but valid suggestions.
However, we found that in some cases, such suggestions provide value when the user is writing code in "exploration mode".
Such suggestions indicate a way of getting something of the desired type.
Now the user has to evaluate if they want to manually call the relevant methods on the builder or if they do not wish to use the builder at all.
Without these suggestions, the user may even not know that a builder exists for the type.
==== Procedural Macros
An interesting observation was that filling holes in the implementation of procedural macros is less useful than usual and can even cause compile errors.
The decrease in usability is caused by procedural macros mapping ```rust TokenStream``` to ```rust TokenStream``` (Rust syntax to Rust syntax), meaning we do not have useful type information available.
This is very similar to the builder pattern, so the decrease in usefulness originates from the same reasons.
However, procedural macros are somewhat special in Rust, and they can also raise compile-time errors.
For example, one can assert that the input ```rust TokenStream``` contains a non-empty `struct` definition.
As the term search has no way of knowing that the ```rust TokenStream``` has to contain certain tokens, it also suggests other options that validate the rule, causing the error to be thrown.
==== Formatting
We found that the formatting of the expressions can have a significant impact on the usability of the term search in cases of autocompletion.
This is because it is common for LSP clients to filter out suggestions that do not look similar to what the user is typing.
Similarity is measured at the level of text with no semantic information available.
This means that even though ```rust x.foo()``` (method syntax) and ```rust Foo::foo(x)``` (universal function call syntax) are the same, the second option is filtered out if the user has typed ```rust x.f``` as text wise they do not look similar.
This causes some problems for our algorithm, as we decided to use universal function call syntax whenever possible, as this avoids ambiguity.
However, users usually prefer method syntax as it is less verbose and easier to understand for humans.
However, this is not a fundamental limitation of the algorithm.
One option to solve this would be to produce suggestions using both of the options.
That, however, has its issues, as it might overwhelm the user with the number of suggestions if the suggestions are text-wise similar.
There can always be options when the user wishes to mix both of the syntaxes, which causes the number of suggestions to increase exponentially as every method call would double the number of suggestions if we would suggest both options.
==== Foreign function interface crates <c-style-stuff>
We found that for some types of crates, the performance of the term search was significantly worse than for others.
It offers a lot more terms per hole by suggesting 303 terms per hole, which is about 15 times more than the average of 20.
Such a large number of suggestions is overwhelming to the user, as 300 suggestions do not even fit on the screen.
Interestingly, almost all of the terms are found at depth 0, and only a very few are added at later iterations.
A high number of suggestions are caused by those crates using only a few primitive types, mostly integers.
For example, in C, it is common to return errors, indexes, and sometimes even pointers as integers.
Yet C's application binary interface (ABI) is the only stable ABI Rust has.
Foreign function interface (FFI) crates are wrappers around C ABI and therefore often use integer types for many operations.
Searching for an integer, however, is not very useful as many functions in C return integers, which all fit into the hole based on type.
For example, the number of terms found per hole reaches 300 already at depth 0, as there are many integer constants that all fit most holes.
This means that there is a fundamental limitation of our algorithm when writing C-like code in Rust and working with FFI crates.
As the point of FFI crates is to serve as a wrapper around C code so that other crates wouldn't have to, we are not very concerned with the poor performance of term search in FFI crates.
To see how the results for crates with idiomatic Rust code would look, we filtered out all crates from the categories "external-ffi-bindings", "os", and "no-std" (@tbl-depth-hyper-param-median).
We can see that _terms per hole_ is the only metric that suffers from C-like code.
#figure(
//placement: auto,
table(
columns: 5,
inset: 5pt,
align: horizon,
table.header[*Depth*][*Holes filled*][*Syntactic matches*][*Terms per hole*][*Average time*],
[0], [19.0%], [2.6%], [1.3], [0.4ms],
[1], [69.1%], [11.1%], [3.9], [6.5ms],
[2], [75.5%], [11.4%], [5.8], [52.1ms],
[3], [76.7%], [11.5%], [7.4], [84.1ms],
[4], [77.0%], [11.4%], [8.0], [99.1ms],
[5], [77.1%], [11.4%], [8.2], [116.0ms],
),
caption: [
Results without crates from categories _external-ffi-bindings_, _os_ and _no-std_.
_Holes filled_, _syntactic matches_ and _average time_ have similar results to overall average.
There are about 14 terms less per hole at all depths.
]
) <tbl-depth-hyper-param-median>
== Limitations of the methods
In this section, we highlight some limitations of our evaluation.
We point out that "holes filled" is a too permissive metric, and "syntactic matches" is too strict.
Ideally, we want something in between, but we don't have a way to measure it.
==== Resynthesis
Metric "holes filled" does not reflect the usability of the tool very well.
This would be a useful metric if we used it as a proof search.
When searching for proofs, we often care that the proposition can be proved rather than which of the possible proofs it generates.
This is not the case for regular programs with side effects.
For them, we only care about semantically correct terms, e.g. do what the program is supposed to do.
Other terms can be considered noise, as they are programs that no one asked for.
Syntactic matches (equality) is a too strict metric as we care about the semantic equality of programs.
The metric may depend more on the style of the program and the formatting than on the real capabilities of the tool.
Syntactic matches also suffer from squashing multiple terms to the ```rust Many``` option, as the new holes produced by _Many_ are not what was written by the user.
Average time and number of terms per hole are significantly affected by a few categories that some may consider outliers.
We have decided not to filter them out to also show that our tool is a poor fit for some types of programs.
Average execution can also be criticized for being irrelevant.
Having the IDE freeze for a second once in a while is not acceptable, even if at other times the algorithm is very fast.
To also consider the worst-case performance, we have decided to also measure latency.
However, we must note that we only measure the latency of our algorithm.
While using the tool in the IDE, the latency is higher due to LSP communication and the IDE also taking some time.
We only measure the latency of our algorithm, as other sources of latency are outside of our control and highly dependent on the environment.
==== Usability
This section is based on the personal experience of the author and may therefore not reflect the average user very well.
Modeling the average user is a hard task on its own and would require us to conduct a study on it.
As studying the usage of IDE tools is outside the scope of this thesis, we only attempt to give a general overview of the strengths and weaknesses of the tool.
Different issues may arise when using the tool in different contexts.
= Future work <future-work>
In this section, we will discuss some of the work that could be done to improve term search in `rust-analyzer`.
Some of these topics consist of features that were not in the scope of this thesis.
Others focus on improving the `rust-analyzer` functionality overall.
==== More permissive borrow checking
The current borrow checking algorithm we implemented for `rust-analyzer` is rather conservative and also forbids many of the correct programs.
This decreases the usefulness of term search whenever reference types are involved.
The goal would be to make the borrow checking algorithm in `rust-analyzer` use parts of the algorithm that are in the official compiler but somehow allow borrow checking also on incomplete programs.
Lowering incomplete programs (the user is still typing) to MIR and performing borrow checking incrementally is a complex problem, however, we believe that many other parts of the `rust-analyzer` could benefit from it.
==== Smarter handling of generics
In projects with hundreds of functions that take generic parameters our algorithm effectiveness decreases.
One of the main reasons for this is that we fully normalize all types before working with them.
In the case of types and functions that have generic parameters, this means substituting the generic parameters.
However, that is always not required.
Some methods on types with generic parameters do not require knowing exact generic parameters and therefore can be used without substituting in the generic types.
Some examples of it are ```rust Option::is_some``` and ```rust Option::is_none```.
Others only use some of the generic parameters of the type.
If not all generic parameters are used, we could avoid substituting the generic types that are not needed, as long as we know that we have some options available for them.
==== Development of more tactics
A fairly obvious improvement that we believe still should be touched on is the addition of new tactics.
The addition of new tactics would allow usage in a new context.
Some ideas for new tactics:
- Tuple projection - very similar to struct projection. Very easy to add.
- Macro call - similarly to function calls, macros can be used to produce terms of unexplored types.
As macros allow more custom syntax and work at the level of metaprogramming, adding them can be more complex.
- Higher-order functions - generating terms for function types is more complex than working with simple types.
On the other hand, higher-order functions would allow the usage of term search in iterators and therefore increase its usefulness by a considerable margin.
- Case analysis - Perform a case split and find a term of suitable type for all the match arms.
May require changing the algorithm slightly as each of the match arms has a different context.
==== Machine learning based techniques
We find that machine-learning-based techniques could be used to prioritize generated suggestions.
All the terms would still be generated by term search and would be valid programs by construction, which is a guarantee that LLMs cannot have.
On the other hand, ordering suggestions is very hard to do analytically, and therefore we believe that it makes sense to train a model for it.
With a better ordering of suggestions, we can be more permissive and allow suggestions that do not affect the type of the term (endofunctions).
For example, suggestions for builder patterns could be made more useful by also suggesting some setter methods.
==== LSP response streaming
Adding LSP response streaming is an addition to `rust-analyzer` that would also benefit term search.
Response streaming would be especially helpful in the context of autocompletion.
It would allow us to incrementally present the user autocompletion suggestions, meaning that latency would become less of an issue.
With the latency issue solved, we believe that term-search-based autocompletion suggestions could be turned on by default.
Currently, the main reason for making them opt-in was that the autocompletion is already slow in `rust-analyzer` and term search makes it even slower.
= Conclusion <conclusion>
In this thesis, our main objective was to implement a term search for the Rust programming language.
We achieved it by implementing it as an addition to `rust-analyzer`, the official LSP server for Rust.
First, we gave an overview of the Rust programming language to understand the context of our work.
We are focusing on the type system and the borrow checking, as they are two fundamental concepts in Rust.
After that, we gave an overview of term search and the tools for it.
We focused on the tools used in Agda, Idris, Haskell, and StandardML.
We analyzed both their functionality and the algorithms they use.
By comparing them to one another, we laid the groundwork for our implementation.
After that, we covered the LSP protocol and some of the autocompletion tools to gain some understanding of the constraints we have when trying to use the term search for autocompletion.
The term search algorithm we implemented is based on the tools used in Agda, Idris, Haskell, and StandardML.
We took a different approach from the previous implementations by using a bidirectional search.
The bidirectional approach allowed us to implement each tactic in the direction that was the most natural fit for it.
This resulted in a rather simple implementation of tactics that achieved relatively high performance.
To evaluate the performance of the algorithm, we ran it on existing open-source projects.
For measuring the performance, we chose the top 5 projects from the most popular categories on crates.io, the Rust community’s crate registry.
This resulted in 155 crates.
We added term-search-based autocompletion suggestions to evaluate the usability of term search for autocompletion.
With its small depth, the algorithm proved to be fast enough and resulted in more advanced autocompletion suggestions compared to the usual ones.
As the autocompletion in `rust-analyzer` is already rather slow, the feature is disabled by default, yet all the users of it can opt into it.
|
|
https://github.com/sitandr/mdbook-typst-highlight | https://raw.githubusercontent.com/sitandr/mdbook-typst-highlight/main/example-book/src/chapter_2.md | markdown | MIT License | # Chapter 2
It uses external Typst that should be installed in path, so you can use packages too!
```typ
#import "@preview/cetz:0.1.2": canvas, plot
#set page(width: auto, height: auto, margin: .5cm)
#canvas(length: 1cm, {
plot.plot(size: (8, 6),
x-tick-step: none,
x-ticks: ((-calc.pi, $-pi$), (0, $0$), (calc.pi, $pi$)),
y-tick-step: 1,
{
plot.add(
style: plot.palette.blue,
domain: (-calc.pi, calc.pi), x => calc.sin(x * 1rad))
plot.add(
hypograph: true,
style: plot.palette.blue,
domain: (-calc.pi, calc.pi), x => calc.cos(x * 1rad))
plot.add(
hypograph: true,
style: plot.palette.blue,
domain: (-calc.pi, calc.pi), x => calc.cos((x + calc.pi) * 1rad))
})
})
```
```typ
$integral_a^b x^2$
#show math.equation: set text(font: "Fira Math", fallback: false)
$integral_a^b x^2$
``` |
https://github.com/qujihan/typst-cv-template | https://raw.githubusercontent.com/qujihan/typst-cv-template/main/README_zh.md | markdown | # 快速上手
```shell
# 将此项目作为git子模块添加
git submodule add https://github.com/qujihan/typst-cv-template.git typst-cv-template
git submodule update --init --recursive
# 实时预览
python typst-cv-template/op.py w
# 编译
python typst-cv-template/op.py c
# 格式化typst代码
python typst-cv-template/op.py f
``` |
|
https://github.com/HarryLuoo/sp24 | https://raw.githubusercontent.com/HarryLuoo/sp24/main/431/notes/part2.typ | typst | #set math.equation(numbering:"(1)")
#set heading(numbering: "1.1")
= Random Variables
#image("rvSummary.png")
== Discrete random variable
Discrete random variables are random variables that can take on a countable number of values. It comes naturally from discrete, finite or infinitly countable sample spaces. (As briefly discussed in sec.discreteSampleSpace)
For $A = {k_1,k_2,...,} $ s.t. random variable$X in A$, or $P(X in A) = 1$, X is a random variable, with possible values $k_1,k_2,...$ and $P(X=k_n)>0$
=== Probability Mass Function (pmf)
The PMF is a function that defines the probability distribution for a discrete random variable. It gives the probability of the random variable taking on each possible value. The PMF, denoted as $ p_X (k) = P(X=k) ", where" k "are possible values of X" $ It is a function of k, and $ p_X : S → [0, 1], $ where:
S is the support set, i.e., the set of all possible values that the discrete random variable X can take.
[0, 1] represents the range of the function, as probabilities are always between 0 and 1.
For each value k in the support set S, the PMF assigns a probability p_X(k), which represents the likelihood of the random variable X taking the value k.
The PMF satisfies the following properties:
Non-negativity: $p_X(k) >= 0$ for all k in S.\
Total probability: $sum_k p_X(k) = 1$ where the sum is taken over all k in S.\
Example: For a fair six-sided die, the PMF would be $P(X = x) = 1/6$ for $x = 1, 2, 3, 4, 5, 6$. Or more elegantly,$ p_X (k)=1/6, "for every" k in {1,2,3,4,5,6} $
== continuous Random Variables
Not rigorously defined in this class, but a continuous random variable is one that can take on any value in a range. The probability of a continuous random variable taking on a specific value is 0.
It came natually from continuous sample spaces.The probability is assigned to intervals of values, and they are assigned by the *probability density function*.
=== Probability Density Function (pdf)
continuous r.v are defined in this class by having a probability density function.\
A random variable X is continuous if there exists a function f(x) such that $
integral_(-infinity)^(infinity) f(x) dif x =1, f(x) >0 "everywhere" \ "and" P(X<=b) = integral_(-infinity)^b f(x) dif x <=> P(a<= X <= b) = integral_a^b f(x) dif x
$
=== Cumulative Distribution Function (cdf)
cdf of a r.v. is defined as $ F(x) = P(X<=x) $
and it follows that $
P(a< X <= b) = P(X <=b) - P(X<=a) = F(b) - F(a)
$ <eq.defCDF>
- Continuous r.v.
it looks suspiciously like an indefinite integral, and when we are dealing with continuous r.v., it is.
#rect(inset: 8pt)[ $
display(F(s) = P(X<= s) = integral_(-infinity)^(s) f(x) dif x
)$ ]
Recall the fundamental theorm of calculus, $ F'(x) = f(x), $ so the pdf is the derivative of the cdf.\
- Discrete r.v.
pmf and cdf is connected by $ F(x) = P(X <= s) = sum_(k<=x) p_X(k) $
where the sum is taken over all k such that $k<=x$.\
In english, the cdf is the sum of the pmf up to the value x, or "compound probability thus far"
If the cdf graph is stepped (piecewise constant), it is a discrete r.v. If it is continuous except at several points, it is a continuous r.v.
== Expectation and Variance
=== Expectation
+ Exp of discrete r.v. is defined as $ E(X) = sum_k k P(X=k) $ where the sum is taken over all possible values of X. It is the weighted average of the possible values of X, where the weights are given by the possible values.
Expectation is a linear operator, i.e. $ E(a X + b) = a E(X) + b $ for any constants a and b.
- exp of *Bernoulli* r.v. is $ E(X) = p $ where p is the probability of success.
- exp of *binomial* r.v. is $ E(X) = n p $ where n is the number of trials and p is the probability of success.
- exp of *geometric* r.v. is $ E(X) = 1/p $ where p is the probability of success.
+ Exp of continuous r.v. is defined as $
E(X) = integral_(-infinity)^(infinity) x f(x) dif x
$
where the integral is taken over the entire range of possible values of X. It is the weighted average of the possible values of X, where the weights are given by the probability density function.
- exp of *uniform* r.v. is $
E(X) = (a+b)/2
$
where a and b are the lower and upper bounds of the interval.
=== Expectation of a function of a random variable
When we have a function of a random variable, we can find the expectation of that function by applying the function to each possible value of the random variable and taking the weighted average of the results.
- if X is a discrete r.v. with pmf p_X(k), and g is a function of X, then $ E(g(X)) = sum_k g(k) p_X(k) $
- if X is a continuous r.v. with pdf f(x), and g is a function of X, then $ E(g(X)) = integral_(-infinity)^(infinity) g(x) f(x) dif x $
=== Moments, and moment generating function
+ The *nth moment* of the random variable X is the expectation $E(X^n)$.
- X as discrete r.v. with pmf p_X(k), the nth moment is $ E(X^n) = sum_k k^n p_X(k) $
- X as continuous r.v. with pdf f(x), the nth moment is $ E(X^n) = integral_(-infinity)^(infinity) x^n f(x) dif x $
+ The *moment generating function* of a
- discrete random variable X is defined as $
M_X (t) = E(e^(t X)) = sum_k e^(t k) p_X(k)
$
- continuous random variable X is defined as $
M_X (t) = E(e^(t X)) = integral_(-infinity)^(infinity) e^(t x) f(x) dif x
$ It is a function of t.
We can easily find the nth moment of X by taking the nth derivative of the moment generating function with respect to t and evaluating it at t = 0. i.e. $ E(X^n) = (dif ^n )/(dif t) M_X (t=0) $
=== Variance
The variance of a random variable X is a measure of how much the values of X vary around the mean. It is defined as the expectation of the squared deviation of X from its mean. i.e. $ sigma^2 = "Var"(X) = E((X - E(X))^2)
$
alternatively, $ "Var"(X) = E(X^2) - (E(X))^2 $
Variance is not a linear operator, i.e. $ "Var"(a X + b) = a^2 "Var"(X) $ for any constants a and b.
+ variance of bournoli r.v. is $ p(1-p) $
+ variance of binomial r.v. is $ n p (1-p) $
+ variance of geometric r.v. is $ (1-p)/(p^2) $
+ variance of uniform r.v. is $ (b-a)^2/12 $
= continuous Distribution
Based on different pdf, we have different behaviors of random variables. We call them distributions.
== Uniform Distribution
r.v. X has the uniform distribution on the interval [a,b] if its pdf is $ f(x) = cases(display(1/(b-a)) "for" a<=x<=b, 0 "otherwise") $
== Normal (Gaussian) Distribution
=== standard normal distribution
r.v. Z has the Standard normal distribution if its pdf is $ f(z) = phi(z) = 1/sqrt(2π) e^(-z^2slash 2) $ where z is the standard normal r.v. and phi is the standard normal pdf.
It's abbrieviated as $Z ~ N(0,1)$ where 0 is the mean and 1 is the variance.
- The *cdf* of the standard normal distribution is denoted as $ Φ(z) = P(Z <= z) = integral_(-infinity)^(z) phi(z) dif z $
Check for table for values of $Φ(z)$
=== normal distribution (generalized)
two parameters: the mean μ and the variance $sigma^2$ . The pdf of a normal distribution is given by the formula:
$ f(x) = 1/(sqrt(2π sigma^2)) exp[-(x-μ)^2/(2σ^2)] $
abbrieviated as $X ~ N(μ,σ^2)$
- Linearity of normal distribution
If $X~ N(mu, sigma^2), Y = a X + b$, then $Y ~ N(a mu + b, a^2 sigma^2)$
- *normalization of normal distribution*
For $X~ N(mu, sigma^2)$, we can standardize it to $Z ~ N(0,1)$ by $Z = (X - mu)/sigma$
= Approximations of Binomial Distribution
Recall: *Binomial distribution* is the distribution of the _number of successes_ of n independent Bernoulli trials. It has two parameters: the number of trials n and the probability of success p.
Depending on the probability of success p and the number of trials n, the binomial distribution can be approximated by the normal distribution or the Poisson distribution.
== Central limit theorem (approximation with normal distribution)
If n is large and p is not too close to 0 or 1, the binomial distribution can be approximated by the normal distribution.
For $S_n ~ "Bin"(n,p) space ; space E(S_n)=n p space , "Var" ( S_n)= sigma^2 = n p(1-p),$
$ lim_(n ->infinity ) P(a <= (S_n - mu )/(sigma) <= b) = integral_(a )^(b ) phi(x) dif x =Phi(b) - Phi(a) $
where phi is the standard normal pdf. This is the central limit theorem, which states that the binomial random variables approaches a normal distribution when $n p (1-p) > 10$ .
=== continuity correction
$
P(a <= S_n <= b) = P(a-0.5 <= S_n <= b+0.5)
$
where S~Bin(n,p) and a,b are integers. Useful when a,b are close, and np(1-p) is not large.
=== Law of large numbers
For $
S_n ~ "Bin"(n,p) space ; space E(S_n)=n p , E(S_n/n) = p\
P(|S_n/n - p| < epsilon) -> 1 "as" n -> infinity
$ In English, this is saying that, as n is large, the frequency of success in n trials will converge to the probability of success p.
=== Confidence interval
In most cases, if real probability of success is unknown, we can use the Law of large number to
1. approximate p
2. find confidence interval $(hat(p)-epsilon, hat(p ) + epsilon )$ (know how accurate the approximation is.)
Connecting law of large number with CLT, we can proof that $
P(|hat(p) - p| < epsilon) >= 2Phi(2epsilon sqrt(n) ) - 1
$
where, $2Phi(2epsilon sqrt(n) ) - 1$ is the confidence level, i.e. how confident we are that the real probability is in the interval.
== Poisson Distribution
=== Poisson r.v.
A discrete r.v. L has the Poisson distribution with parameter λ>0 if its pmf is $
p_L (k) = e^(-λ) λ^k/k!
$ for k = 0, 1, 2, ...
- write $L ~ "Poisson"(lambda)$
- The mean and variance of a Poisson r.v. are both equal to λ.
=== Law of rare events
For $S_n ~ "Bin"(n, lambda/n), "where" lambda/n <1$, S_n follows the law of rare events,
$
lim_(n -> infinity) P(S_n = k) = e^(-lambda) lambda^k/k!
$
The distribution Bin($n,lambda/n$ ) approaches Poisson($lambda$) distribution, where $E(S_n) = lambda$
For a fixed n, to quantify the error in approximation, we have:
Let X~Bin(n,p), and Y~Poisson($lambda$), where $lambda = n p$
then for any subset $ A subset.eq {0,1,2,...,n}, k in A \
|P(X = k) - P(Y = k)| <= n p ^2
$
if $n p ^2 <1$, then the approximation is good, and that $
P(X =k ) approx P(Y = k)= e^(-lambda) lambda^k/k!
$
== Exponential Distribution
No mentioning where it comes from, but will be told when "can be modeled by exponential distribution"
A continuous r.v. X has the exponential distribution with parameter λ>0 if its pdf is $
f(x) = cases(display(λ e^(-λ x)) "for" x>=0, 0 "otherwise")
$
Write $X ~ "Exp"(lambda)$
The cdf is found by integrating the pdf, $
F(x) = cases(display(1 - e^(-λ x)) "for" x>=0, 0 "otherwise")
$
Notice the tail probability, $
P(X>t) = e^(-lambda t)
$
Expectations and variance are
$
E(X) = 1/lambda , "Var"(X) = 1/lambda^2
$
- EXp distribution is memoryless, i.e. $ P(X > t+s | X > t) & = P(X> t+s, X >t)/P(X>t) \
& = P(X>t+s)/P(X>t) \
& = (e^(-lambda(t+s)) )/(e^(-lambda t) ) \
& = e^(-lambda s) \
& = P(X>s)
$ for all s,t > 0
= Joint Distribution
== discrete joint distribution
- definition: $
p(k_1, k_2,k_3) = P(X_1 = k_1, X_2 = k_2, X_3 = k_3)
$ for r.v. $X_1 = k_1, X_2=k_2, X_3=k_3$
- expectation:
$
E(g(X_1, X_2, X_3)) = sum_(k_1) sum_(k_2) sum_(k_3) g(k_1, k_2, k_3) p(k_1, k_2, k_3) $
- marginal distribution:
$
p_1(k) = sum_(k_2) sum_(k_3) p(k, k_2, k_3)
$
- Multinomial distribution
when looking for the probability of some independent events together, we can use the multinomial distribution.
$
P(X_1 = k_1, X_2 = k_2, X_3 = k_3) = n!/(k_1 ! k_2 ! k_3 !) p_1^(k_1) p_2^(k_2) p_3^(k_3)
$
abbreviate this as $(X_1,X_2,...,X_r) ~ "Multi"(n,r,p_1,p_2,...,p_r)$
== Continuous joint distribution
- definition: $
P((X_1,X_2,X_3) in A) = integral_(A) f(x_1, x_2, x_3) dif x_1 dif x_2 dif x_3
$ for r.v. $X_1, X_2, X_3$ and set $A in Re$
- expectation: $
E(g(X_1, X_2, X_3)) = integral_(-infinity)^(infinity)integral_(-infinity)^(infinity)integral_(-infinity)^(infinity) g(x_1, x_2, x_3) f(x_1, x_2, x_3) dif x_1 dif x_2 dif x_3
$
- marginal distribution: $
f_1(x) = integral_(-infinity)^(infinity)integral_(-infinity)^(infinity) f(x, y, z) dif y dif z
$
== Independent joint random variables
- Necessary and sufficient Condition:
- discrete $
p(x_1, x_2) = p_1(x_1) p_2(x_2)
$
- Continuous $
f(x_1, x_2) = f_1(x_1) f_2(x_2)
$
- If two r.v. depend on different parameters, they are independent. i.e. $
Y=f(X_1,X_2,X_3); quad Z=g(X_(4),X_(5),X_6)\ => Y "and" Z "are independent"
$
|
|
https://github.com/LEXUGE/poincare | https://raw.githubusercontent.com/LEXUGE/poincare/main/src/notes/quantum-mechanics/main.typ | typst | MIT License | #import "@preview/physica:0.9.2": *
#import "@preview/gentle-clues:0.8.0": *
#import "@preview/ctheorems:1.1.0": *
#import "@lexuge/templates:0.1.0": *
#import shorthands: *
#import pf3: *
#show: simple.with(
title: "Quantum Mechanics", authors: ((name: "<NAME>", email: "<EMAIL>"),),
)
#show: super-plus-as-dagger
#let op(body) = $hat(body)$
#let vecop(body) = $underline(hat(body))$
#let ft(body, out) = $cal(F)[body](out)$
#let invft(body, out) = $cal(F)^(-1)[body](out)$
#let inv(body) = $body^(-1)$
#let iff = $<==>$
#let implies = $=>$
#let spinup = $arrow.t$
#let spindown = $arrow.b$
#let pm = $plus.minus$
#let mp = $minus.plus$
#pagebreak()
= Preface
== Rigor
Quantum Mechanics has somewhat deep mathematics#footnote[In fact even electrodynamics do.] if
you are willing to dig into (even Hilbert space theory alone is not enough). I
admit I don't have enough familiarity on these mathematical details. *And I will
not pretend I do in order _not_ to create an illusion.*
What I hope to achieve is to have a somewhat logical formulation of the theory
and point out _some_ mathematical subtleties that I have been told or seen.
Specifically, my criterion for rigor is:
1. Statements and theorems should be proven in finite-dimensional vector spaces.
2. We neglect some analytical problems like Dirac delta "function", provided we
have intuition and analogue developed from finite-dimensional counterparts.
3. However, any algebraic picture should be made as much clear as possible. We
should clearly define the algebraic structure and objects that we are
manipulating#footnote[However, we have to use intuition when necessary for, e.g. vector operator due
to lack of representation theory.].
However, I shall come back later to fill out mathematical details in the long
run (hope I do).
/*
= Mathematical Formulation & Postulates
There are few main goals on mathematics:
- Define the symbol $dagger$ on different objects#footnote[This is a heavily "overriden" operator and sadly not a lot of books talk about
this in details]. And prove various properties in finite-dimensional Hilbert
space (i.e. finite-dimensional complex vector spaces).
- Understand how and _why_ to use Dirac notation (i.e. why is it useful).
- State various spectral theorems and understand (at least partially) what goes
wrong in infinite dimensions.
Then we will state the postulates for quantum mechanics.
This part follows fairly closely to @littlejohn's notes 1,2,3,4 as I found no
book explaining more satisfactory than he does. I will also reference to @isham
and @binney later on.
== Hilbert Space and Dirac Notation
For our purpose, we will think of Hilbert space _very roughly_ as:
#def(
"Hilbert Space",
)[
We think of Hilbert space as a complex vector space $V$ with an inner product $angle.l dot.c , dot.c angle.r$ and
a countable orthonormal basis. This means (for our purpose) there exists a
vector sequence ${vb(v)_i}$ such that for all $vb(v) in V$, there exists a
unique sequence ${c_i in CC}$ such that#footnote[We neglect convergence details]
$ vb(v) = sum_(i=1)^infinity c_i vb(v)_i $
]
#info[Mathematically a vanilla Hilbert space will not satisfy our "definition" above.
We need further assumptions like "separable". However, the Hilbert space we deal
with (or construct) are indeed mostly separable. And adding this extra notion
will not help us understand more as we don't have enough mathematics to
appreciate it anyway.]
And we basically treat Hilbert space as if it is finite dimensional until we
reach spectral theorems where we give a few complication examples (as they are
the complication that will come into our "calculation").
Therefore, we will construct our theory mostly in a finite-dimensional complex
vector space setting, and just "generalize" (with hope) to infinite-dimensional
Hilbert space.
Our first task is to setup dual space as this is where Dirac notation comes
alive.
#def(
"Dual Space",
)[
Define the dual space $V^*$ of a vector space $V$ as the space of all linear
functionals:
$ V^* := { f: V arrow.r CC } $
]
If $V$ is finite dimensional, from well known results in finite dimensional
linear algebra, we know $dim V = dim V^*$, and $V$ is naturally isomorphic to $V^(**)$ with
the "application mapping" $i: V arrow.r V^(**)$:
$ underbracket(i(vb(v)), V^(**))(f in V^*) = f(vb(v)) $
If we have an inner product structure on $V$, then we further have an
*antilinear* natural identification $dotless.i: V arrow.r V^*$ defined by
$ underbracket(ii(vb(v)), V^*)(vb(u)) = angle.l vb(v), vb(u) angle.r $
Note this is antilinear:
$ ii(c vb(v)) = angle.l c vb(v), dot.c angle.r = c^* al vb(v), dot.c ar = c^* ii(vb(v))$.
#warning[
We will denote different operators like $ii_V: V to V^*$ and $ii_W: W to W^*$ with
the same symbol $ii$. It should be understood in context.
]
Now, we define transpose of a linear mapping. Even though we will be dealing
with mappings that maps into itself, we shall define transpose for a general
mapping across different space just for slightly better clarity.
#def(
"Transpose",
)[
Let $hat(A): V arrow.r W$ be a linear mapping between vector spaces $V,W$. We
define transpose $hat(A)^t: W^* to V^*$ as#footnote[$hat(A)^t$ here is not a standard mathematics notation]
$ underbracket(hat(A)^t (f in W^*), V^*) = f compose hat(A) $
]
#info[We are adding $hat$ to denote operators/mapping in order to be consistent with
later notations. Later we will find ourselves writing "quantum-number",
eigenvector, and operator all with the same alphabet. So having accent to
distinguish is necessary. But when not useful, we will also suppress it to
reduce notation clutter.]
#thm("Transpose of Transpose is Itself")[
We have $(A^t)^t = A$.
]
#proof[
By definition $(A^t)^t vb(v) = vb(v) compose A^t$. And we basically want to
prove $vb(v) compose A^t = A vb(v)$ under canonical identification. For all $f in V^*$,
$ (A vb(v))(f) = f(A vb(v)) = (f compose A)(vb(v)) $
while
$ (vb(v) compose A^t) (f) &= vb(v) (A^t f) \
&= vb(v) (f compose A) = (f compose A)(vb(v)) $
]
And we also have adjoint of an operator defined in the usual way using inner
product.
#def(
"Adjoint",
)[
The adjoint of $A: V to W$, denoted as $A^dagger: W to V$ is defined using "matrix
elements" as
$ al A^dagger vb(w), vb(v) ar_V = al vb(w), A vb(v)ar_W $
for any $vb(w) in W, vb(v) in V$
Alternatively, this could be written as
$ (ii compose A^dagger)(vb(w))(vb(v)) &= ii(vb(w))(A(vb(v))) \
&= (ii(vb(w)) compose A)(vb(v)) \
&= (A^t compose ii)(vb(w))(vb(v)) $
So $ii_V compose A^dagger = A^t compose ii_W$ to be more accurate. And with
canonical identification between $V, V^(**)$, we can further write
$ II compose A^dagger = ii_(V^*) compose ii_V compose A^dagger= ii_(V^*) compose A^t compose ii_W $
] <defn-adjoint>
#warning[
Matrix of $A^dagger$ is conjugate transpose of matrix of $A$ only under
orthonormal basis. This is because only then would $al vb(v)_i, cdot ar$ give
you the coordinate under basis ${vb(v)_i}$.
]
You may already find notation cluttering. And this is where Dirac notation
becomes helpful.
#def(
"Dirac Notation",
)[The rules are followings
- We use $ket(cdot)$ to denote a vector and $bra(cdot)$ to denote a linear
functional. The content in the middle can be anything that we use to identify
the vector#footnote[This is especially useful to solve alphabet shortage e.g. we could write $ket(+)$ to
denote a vector without causing confusion with the actual $+$ operator.].
- If the content inside is the same, we understood they are related by $ii$. e.g. $bra(p) = ii(ket(p))$.
- We shorten the notation $bra(a) (ket(b))$ into $braket(a, b)$. So $braket(a, b)$ should
be understood as the application of linear functional $bra(a)$ on $ket(b)$. And
because of identification, this is also $ii(ket(a))(ket(b)) = al ket(a), ket(b) ar$.#footnote[This is why people often think $braket(a, b)$ is just a notation for inner
product. *But it's better not to think like this.*]
- We create a linear mapping by $ketbra(a, b): V to V$, this is understood as the
mapping defined by
$ underbracket(ketbra(a, b), V to V) underbracket(ket(phi), V) = ket(a) underbracket(braket(b, phi), CC) $
]
An important remark to make is on the last point. It seems natural to also
define $ketbra(a, b)$ as $V^* to V^*$ by "applying it from the right":
$ ketbra(a, b) (bra(phi)) := braket(phi, a) bra(b) $
So how should we understand this? The answer is to use the concept of transpose.
#def(
"Operators act according to their types",
)[Because of the definition of the transpose, for $A: V to V$,
$ bra(psi) (hat(A) ket(phi)) = underbracket((hat(A)^t bra(psi)), V^*) ket(phi) $<transpose-dirac>
So if we invent the fifth rule: *operators act according to their type*, then
transpose should apply to the "bra" on the left which are linear functionals.
Thus we can write:
$ bra(psi) hat(A) ket(phi) = bra(psi) hat(A)^t ket(phi) $
which should be understood as @transpose-dirac.]
Now, the transpose of $ketbra(a, b)$ is given by
$ ketbra(a, b)^t (bra(psi)) (ket(phi)) &= bra(psi) (ketbra(a, b) ket(phi)) "By definition of transpose" \
&= braket(b, phi) bra(psi) (ket(a)) \
&= braket(b, phi) braket(psi, a) $
So fix $bra(psi)$ and vary $ket(phi)$. Since this is true for all $ket(phi)$, by
positive-definiteness of inner product,
$ ketbra(a, b)^t (bra(psi)) = braket(psi, a) bra(b) $
And use the *transpose act to the left rule*, we can then write
$ bra(psi) (ketbra(a, b))^t = braket(psi, a) bra(b) $
Moreover, due to definition of transpose (the operators in the following
equation should act on left/right according to previous rules),
$ underbracket(bra(psi) (ketbra(a, b))^t, "act first") ket(phi) = bra(psi) underbracket((ketbra(a, b)) ket(phi), "act first") $
_And we may actually drop the transpose even_, whenever we encounter an
expression,
$ bra(psi) hat(A) ket(phi) $
It is understood as:
- $hat(A)$ acts on the side according to its type.
- We may change the side by taking transpose of $hat(A)$ and then act on the other
side first. The result will be the same by definition of transpose.
#info[
And this is why when people writing Dirac notation, they just take together "bra"
and "ket" eagerly without thinking about the syntax, because they can. In
particular, when people see
$ bra(psi) ketbra(a, b) $
they will automatically write $braket(psi, a) bra(b)$. But what they really did
is implicitly take the transpose of $ketbra(a, b)$ and act on $bra(psi)$. And
everything works because $ketbra(a, b)^t bra(psi) = braket(psi, a) bra(b)$.
This is also why this notation is powerful: most things you feel natural is
indeed correct.
]
#warning[
However, when you see $bra(psi) hat(A)$ where $A: V to V$, you should not act on
the left because the type doesn't even match!
This is why you feel operators only can apply to the right.
]
Up till now, you shall see how the identification of $V, V^*$ is built-in into
the Dirac notation. And sort of we could pair-up the neighboring term and move
scalar around.
We have one notion not yet integrated to the Dirac notation: adjoint.
Again, even if we deal with only one single space in real life, it's easier to
illustrate the concept if we have generic $A: V to W$.
By definition, we know from @defn-adjoint that
$ al A^dagger vb(w), vb(v) ar_V = al vb(w), A vb(v)ar_W $
use the $ii$ and translate into Dirac notation, we have equivalently the
definition
$ bra(vb(v)) A^dagger ket(vb(w))^* = bra(vb(w)) A ket(vb(v)) $ <adjoint-in-dirac>
Notice in the Dirac notation, it's _literally impossible_ to have $A^dagger$ act
on the left to write something like
$ bra(vb(w)) A^dagger ket(vb(v)) "This is wrong" $ <wrong-adjoint>
Because:
- $A^dagger: W to V$ cannot act on left which is in $W^*$.
- $A^dagger: W to V$ cannot act on the right which is in $V$.#footnote[This is why I want to illustrate in different spaces.]
So @wrong-adjoint is basically meaningless.
#info[
And this is *why you should not interpret braket as another name for inner
product*. Cause if it's inner product then you can indeed think of
$ bra(vb(w)) A^dagger ket(vb(v)) = al A^dagger vb(w), vb(v) ar $
And you don't know what to write for
$ al vb(w), A vb(v) ar =^? bra(vb(w)) A ket(vb(v)) $
unless you remember some unnatural "which-side-to-act" convention.
]
And finally, we do an operator overloading. Define $dagger$:
- $z^dagger = z^*$ for $z in CC$.
- $ket(phi)^dagger = ii(ket(phi))$.
- adjoint for operators.
Using these definitions, we write @adjoint-in-dirac as
$ bra(vb(v)) A^dagger ket(vb(w))^dagger = bra(vb(w)) A ket(vb(v)) $
which is what people always do: _apply $dagger$ to each constituent according to the rules above and inverse
their order_.
In particular,
$ (ketbra(a, b))^dagger = ketbra(b, a) $
This can be formally seem by appealing to
$ ketbra(a, b)^dagger = ii compose ketbra(a, b)^t compose ii $
So for all $ket(phi)$,
$ ketbra(a, b)^dagger &= ii compose ketbra(a, b)^t (bra(phi)) \
&= ii (braket(phi, a) bra(b)) \
&= ket(b) braket(a, phi)\
&= ketbra(b, a) (ket(phi)) $
Thus $ketbra(a, b)^dagger = ketbra(b, a)$.
With these preparations, you should no longer be feeling like Dirac notation
being just a weird replacement for inner product with some ad-hoc rules.
And things like
$ (hat(H) ket(phi))^dagger = bra(phi) hat(H)^dagger = (hat(H)^dagger)^t bra(phi) $
should feel meaningful.
#info[
Dirac notation from another perspective can also be viewed as some type $(1,1), (0,1), (1,0)$ tensors.
And it works well for such low rank tensors as:
- things can be written in oneliner.
- tensor contraction can only come from left and right. And how to contract is
very natural with these angle brackets (_You won't want to contract $ketbra(a,
b)$ don't you?_).
- We can use "dumb rule" like take "adjoint on each and reverse order" to operate.
]
*/
#pagebreak()
= Postulates and Basic Frameworks
The mathematics of tensors and linear algebras as well as Dirac notation are
covered in my mathematical methods notes.
We all know quantum mechanics is set upon Hilbert space, and tensor product is
involved in the formalism. This section is primarily set to address two
problems:
1. What Hilbert space are we using? How to determine the Hilbert space? (This is
mainly due to @littlejohn[Notes 3])
2. Why does tensor product come into our formalism? When do we divide our spaces
into subspaces tensored together?
But before answering these questions, we should first lay out the postulates of
Quantum Mechanics.
== Postulates
#def[Postulates of the Quantum Mechanics][
We postulates:
1. The states of the quantum system is described by some Hilbert space $cal(H)$.
The state of the system is given by a ray
$ span { ket(phi) in cal(H) } $
2. Any physical observable $A$ is represented by some Hermitian operator $op(A): cal(H) to cal(H)$ on $cal(H)$#footnote[As said in the preface, we neglect the issue about the domain of such operator
(see @bowers[Sec 2.3.3] on why we don't want to care), and the distinction
between Hermitian and self-adjoint that math books may care] The possible
measurement outcomes are the (real) eigenvalues ${A_i}$ of $op(A)$.
3. The probability of measuring eigenvalue $A_i$ of $op(A)$ upon state $ket(phi)$ is
$ PP(A_i) equiv PP(A = A_i) = (||op(P)_A_i ket(phi)||^2) / (||ket(phi)||^2) $
where $op(P)_A_i$ is the projection operator that projects onto the eigenspace
corresponding to the eigenvalue $A_i$. It's easy to see that by linearity of $op(P)_A_i$ that
any vector in the ray will yield the same probability $PP(A_i)$
4. Upon the measurement, the system collapses into the state (ray)
$ span { op(P)_A_i ket(phi) } $
Again, any $ket(phi)$ in the original state (ray) will give the same ray after
collapse.
]<postulates>
In practice, we often work with unit vectors only. Still, two unit vectors
differed by a phase factor are in the same ray, and thus the same physical
state.
From the postulates, it's evident that the order of measurement does matter, so
we need to have notation to distinguish between these cases. We thus write
things in ordered pair to distinguish the order:
$ PP(A = A_i, B= B_j) $
means the probability of measuring $op(A)$ first and $op(B)$ second while
obtaining $A_i, B_j$.
$ PP(A = A_i, A= A_j) $
means the probability of measuring $op(A)$ twice while obtaining $A_i, A_j$ consecutively.
Note this has probability $0$ by our postulates. When we have different state,
we will use subscript to emphasize which state our probability of measurement is
referring to
$ PP_ket(phi)(cdot), PP_ket(psi)(cdot) $
Immediately upon the postulates, we are encountered with the question: _What Hilbert space?_ This
is what we try to answer in the next section.
== Complete Set of Commutative Operators
<csco-procedure>
The idea is simple. We can show that two commutative operators, say $op(A), op(B)$,
has a set of simultaneous eigenspaces. And
1. if we measure $op(A)$ on $ket(phi)$ first, then we will obtain a measurement
outcome $A_i$, with state afterwards $ket(phi') = op(P)_A_i ket(phi)$.
2. if we then measure $op(B)$ on $ket(phi')$, by the mathematical property of
commutative operator, the state afterwards will still be in eigenspace $cal(H)_A_i$.
And if we happen to measure two different outcomes using $op(B)$ on $ket(phi')$ then
we are assured that we have degeneracy in this subspace $cal(H)_A_i$.
3. if we found degeneracy using $op(B)$, we add it to our set of commutative
operators.
4. we can continue this process until we cannot find a new operator (measurement)
that both commutes with the existing set of commutative operators and reveals
degeneracy. In that case, we declare all mutual eigenspaces are non-degenerate,
and we had a *complete set of commutative operator (CSCO)*. And the mutual
eigenbasis (since we assume there is no degeneracy, we call it an eigenbasis)
spans the Hilbert space for our quantum system.
This process is at least in principle experimentally doable. The key is that we
can infer commutativity of measurement from commutativity of the probability.
Now, we fill in all the necessary gaps and theorems for the above procedure to
work.
#thm[Commutative Operators #iff shared Eigenspaces][
Let $op(A), op(B): V to V$ be two diagonalizable linear operators on
finite-dimensional vector space $V$. $[op(A), op(B)] = 0$ if and only if there
exists a complete set of subspaces ${V_i}_(i=1)^r$ that are eigenspaces to both $op(A)$ and $op(B)$.
]<commutative-sim-eigenspaces>
#proof[
#pfstep[Shared Eigenspaces $implies [op(A), op(B)] = 0$][
#pfstep[Every vector admits an unique decomposition: $vb(v) = sum_(i=1)^r vb(v_i) in V_i $][Subspace ${V_i}$ are linearly independent and spanning $V$ by assumption]
#pfstep[$[op(A), op(B)] = 0$][
Since $vb(v_i)$ are all in eigenspaces of $op(A), op(B)$. Let ${A_i}, {B_i}$ be
eigenvalues of $op(A), op(B)$ on ${V_i}$.
$
(op(A)op(B) - op(B)op(A)) vb(v) &= (op(A)op(B) - op(B)op(A)) sum_(i=1)^r vb(v_i) \
&= sum_(i=1)^r B_i op(A) vb(v_i) - A_i op(B) vb(v_i) \
&= sum_(i=1)^r B_i A_i vb(v_i) - A_i B_i vb(v_i) = vb(0)
$
Thus $[op(A), op(B)] = 0$
]
]
#pfstep(
finished: true,
)[$[op(A), op(B)] = 0 implies$ Shared Eigenspaces][
Let ${A_i}$ be eigenvalues of $op(A)$, $V_A_i$ be corresponding eignespaces.
#pfstep[$op(B) V_A_i subset V_A_i$][
Let $vb(v) in V_A_i$, by commutation relation,
$ op(A) op(B) vb(v) - op(B) op(A) vb(v) &= op(A) op(B) vb(v) - A_i op(B) vb(v) \
&= (op(A) - A_i II) op(B) vb(v) = vb(0) $
Thus $op(B) vb(v) in V_A_i$.
]
#pfstep[The restriction of $op(B)$ on $V_A_i$ is still diagonalizable][
#pfstep[Components of eigenvectors of $op(B)$ remains an eigenvector][
Let $vb(v)$ be an eigenvector of $op(B)$ with eigenvalue $lambda$. We can
decompose $vb(v)$ into
$ vb(v) = sum_(i=1)^r vb(v)_i in V_A_i $
And
$ sum_(i=1)^r op(B) vb(v)_i in V_A_i = sum_(i=1)^r lambda vb(v)_i in V_A_i $
By linear independence of subspaces ${V_A_i}$, we know
$ op(B) vb(v)_i = lambda vb(v)_i $
for all $vb(v)_i$.
]
Let ${B_j}_(j=1)^s$ be eigenvalues of $op(B)$ with ${V_B_j}$ as their
corresponding eigenspaces. Let $op(P)_A_i$ be the projection operator that
projects some vector $vb(v)$ onto its component in $V_A_i$. Fix $i$ for now.
#pfstep[${op(P)_A_i V_B_j}$ are linearly independent][
By previous step, we know for any $vb(v) in V_B_j$, $op(P)_A_i vb(v) in V_B_j$ still.
Thus let any $vb(w)_j in op(P)_A_i V_B_j subset V_B_j$ such that
$ sum_(j=1)^s vb(w)_j in V_B_j = vb(0) $
By linear independence of $V_B_j$ we have $vb(w)_j = vb(0)$ for all $j$. Thus ${op(P)_A_i V_B_j}$ are
linearly independent.
]
#pfstep[$plus.circle_(j=1)^s {op(P)_A_i V_B_j} = V_A_i$. So ${op(P)_A_i V_B_j}$ spans $V_A_i$.][
Let $vb(v) in V_A_i$, decompose it into $V_B_j$,
$ vb(v) = sum_(j=1)^s vb(v)_j in V_B_j $
Then
$ vb(v) = op(P)_A_i vb(v) = sum_(j=1)^s op(P)_A_i vb(v)_j in op(P)_A_i V_B_j $
]
These means eigenspaces ${op(P)_A_i V_B_j}$ clearly "factors" $V_A_i$.
]
Now make $i$ arbitrary,
#pfstep[${op(P)_A_i V_B_j}_(i,j=1)^(i=r,j=s)$ is linearly independent][
Let ${vb(v)_(i,j) in op(P)_A_i V_B_j}$ such that
$ sum_(i,j) vb(v)_(i,j) = vb(0) $
We can regroup the sum,
$ sum_(i) underbrace(sum_j vb(v)_(i,j), in V_A_i) = vb(0) $
By linear independence of $V_A_i$, we know for all $i$
$ sum_j vb(v)_(i,j) = vb(0) $
Now by linear independence of $V_B_j$, we know _also_ for all $j$,
$ vb(v)_(i,j) = vb(0) $
]
#pfstep[${op(P)_A_i V_B_j}_(i,j=1)^(i=r,j=s)$ spans $V$][
This is evident as ${op(P)_A_i V_B_j}_(j=1)^s$ spans $V_A_i$ and ${V_A_i}$ spans
the $V$.
]
Thus ${op(P)_A_i V_B_j}$ is the shared eigenspaces that we are after.
]
]
#remark[
There is no statement from this theorem on whether the shared eigenspaces are
gonna be unique. In fact, let $op(A) = II$, we have any set of eigenspaces of $op(B)$ being
shared.
]
Next another useful conclusion
#thm[$[op(A), op(B)] = 0$ #iff $[op(P)_A_i, op(P)_B_j] = 0$ for all $i,j$]<commute-equiv-prj-commute>
#proof[
#pfstep[$[op(A), op(B)] = 0$ #implies $[op(P)_A_i, op(P)_B_j] = 0$ for all $i,j$][
Let $vb(v)$ be arbitrary, fix $i$.
#pfstep[$op(P)_A_i op(P)_B_j vb(v)$ is the component of $op(P)_A_i vb(v)$ in $V_B_j$][
By @commutative-sim-eigenspaces, $op(P)_A_i op(P)_B_j vb(v) in V_B_j$ and
$ sum_(j=1)^s op(P)_A_i op(P)_B_j vb(v) = op(P)_A_i vb(v) $
By linear independence of $V_B_j$, we know $op(P)_A_i op(P)_B_j vb(v)$ is _the_ component
of $op(P)_A_i vb(v)$ in $V_B_j$.
]
By definition, $op(P)_B_j op(P)_A_i vb(v) in A_i$ is the component of $op(P)_A_i vb(v)$ in $V_B_j$.
Since such component is unique, we have
$ op(P)_A_i op(P)_B_j vb(v) - op(P)_B_j op(P)_A_i vb(v) = vb(0) $
]
#pfstep(
finished: true,
)[$[op(P)_A_i, op(P)_B_j] = 0$ for all $i,j$ #implies $[op(A), op(B)] = 0$][
By definition, we have
$ op(A) = sum_i A_i op(P)_A_i, op(A) = sum_j B_j op(P)_B_j $
And since $[op(P)_A_i, op(P)_B_j] = 0$ for all $i,j$,
$ op(A)op(B) &= sum_(i,j) A_i B_j op(P)_A_i op(P)_B_j \
&= sum_(i,j) A_i B_j op(P)_B_j op(P)_A_i \
&= op(B)op(A) $
]
]
#remark[
The projection operator here are not doing orthogonal projection! They are
defined using a set of subspaces. In general, orthogonal projection always
commute, while subspace projection doesn't always commute.
]
We have for projection (either subspace or orthogonal), that
$ op(P)^2 equiv op(P) compose op(P) = op(P) $
And orthogonal projections are Hermitian. Note that for Hermitian operators,
their subspace projection is also orthogonal (and thus also Hermitian)!
#thm[Commutative Measurements #iff Commutative Probability][
$[op(A), op(B)]=0$ if and only if for any eigenvalue $A_i, B_j$ of $op(A), op(B)$ and
any state $ket(phi)$,
$ PP_ket(phi)(A_i, B_j) = PP_ket(phi)(B_j, A_i) $
]
#proof[
By @postulates, we have
$ PP_ket(phi)(A_i, B_j) &= PP_(op(P)_B_j ket(phi))(A_i) PP_ket(phi) (B_j) \
&= (braket(phi, op(P)_A_i op(P)_B_j op(P)_A_i, phi)) / (braket(phi, op(P)^2_B_j, phi)) (braket(phi, op(P)^2_B_j, phi)) / (braket(phi, phi)) \
&= (braket(phi, op(P)_A_i op(P)_B_j op(P)_A_i, phi)) / (braket(phi, phi)) $<eq-prob-A-B>
Similarly,
$ PP_ket(phi)(A_i, B_j) = (braket(phi, op(P)_B_j op(P)_A_i op(P)_B_j, phi)) / (braket(phi, phi)) $<eq-prob-B-A>
#pfstep[For any $ket(phi), A_i, B_j$, $PP_ket(phi)(A_i, B_j) = PP_ket(phi)(B_j, A_i)$ #implies $[op(A), op(B)]=0$][
Since these are equal for all $ket(phi)$, we have
$ op(P)_B_j op(P)_A_i op(P)_B_j = op(P)_A_i op(P)_B_j op(P)_A_i $<eq-origin>
Multiply both sides from left by $op(P)_A_i$ and use $op(P)^2_A_i = op(P)_A_i$,
we have
$ op(P)_A_i op(P)_B_j = (op(P)_A_i op(P)_B_j)^2 = op(P)_A_i op(P)_B_j op(P)_A_i $
Similarly, we can obtain from @eq-origin
$ op(P)_B_j op(P)_A_i =op(P)_B_j op(P)_A_i op(P)_B_j $
Now, by @eq-origin again,
$ op(P)_B_j op(P)_A_i = op(P)_A_i op(P)_B_j $
Since this is true for all $i,j$, by @commute-equiv-prj-commute we have $[op(A), op(B)] = 0$.
]
#pfstep(
finished: true,
)[$[op(A), op(B)]=0$ #implies for any $ket(phi), A_i, B_j$, $PP_ket(phi)(A_i, B_j) = PP_ket(phi)(B_j, A_i)$][
By @commute-equiv-prj-commute, we have $[op(P)_A_i, op(P)_B_j] = 0$ for all $i,j$,
this means
$ op(P)_B_j op(P)_A_i op(P)_B_j = op(P)_A_i op(P)_B_j op(P)_A_i $
As we can commute all projection operators around, and use $op(P)^2 = op(P)$.
Thus @eq-prob-A-B and @eq-prob-B-A are equal for all $i,j, ket(phi)$.
]
]
#remark[
This is experimentally testable if we repeat the experiments with the same state
to collect the statistics, and survey all possible states.
]
#warning[
The condition "for any state $ket(phi)$" is necessary. Otherwise we could
falsely prove $op(S)_x$ commutes with $op(S)_z$ in Stern-Gerlach experiments.
Specifically, let initial state be $ket(y+)$ (eigenvector of $op(S)_y$), then
measure $op(S)_x, op(S)_z$ in both order, we have all outcomes having the same
probability $1/4$.
]
And an extension to @commutative-sim-eigenspaces is
#thm[Pairwise Commutative Operators #iff shared Eigenspace][
Let ${ op(O)_i: V to V }$ be a set of operators. They are pairwise commutative
if and only if they share a complete set of eigenspaces.
]
#proof[
If they share complete set of eigenspaces, then they are evidently commutative.
For the other direction, let $op(A), op(B), op(C)$ be pairwise commutative. Then ${ op(P)_A_i V_B_j }$ is
a shared set of eigenspaces for $op(A), op(B)$. We have
#pfstep(
finished: true,
)[$op(C) op(P)_A_i V_B_j subset op(P)_A_i V_B_j$][
We have $op(P)_A_i V_B_j subset V_A_i$, thus for all $vb(v) in op(P)_A_i V_B_j$, $[op(A), op(C)] = 0$ gives
$ (op(A) op(C) - op(C) op(A)) vb(v) = (op(A) - A_i II) op(C) vb(v) $
And similarly, $op(P)_A_i V_B_j subset V_B_j$, and for all $vb(v) in op(P)_A_i V_B_j$ with $[op(B), op(C)] = 0$ gives
$ (op(B) op(C) - op(C) op(B)) vb(v) = (op(A) - B_j II) op(C) vb(v) $
But $op(P)_A_i V_B_j$ is the only eigenspace with eigenvalue $A_i, B_j$, thus $op(C) vb(v) in op(P)_A_i V_B_j$.
]
Then the rest of the steps are similar to @commutative-sim-eigenspaces: prove ${op(P)_C_k op(P)_A_i B_j}$ are
linearly independent and spans $V$.
This argument genenralizes to finite number of observables.
]
== Tensor Product
Some operators are nicer than others. For certain operators ${op(A), op(B), op(C)}$,
it's possible that any of their individual eigenstates tensored together will
give a set of mutual eigenstates for all operators. This is true for e.g. ${op(x), op(y), op(z)}$ and ${op(x), op(y), op(z), op(S)_z}$.
Apparently, the necessary condition for such thing to happen is that they should
all be pairwise commutative. _However, this is not sufficient for such tensor product structure to happen._ For
example, the spin magnitude operator $[op(S^2), op(S)_z] = 0$, but they don't
exhibit such structure. Their mutual eigenstates are labeled collectively by $ket((s, m))$ with
condition $-s lt.eq m lt.eq s$#footnote[More condition applies to what values $s,m$ can take.].
#info[Hypothesis: if it happens that the individual eigenvalues used to label a (or
for all?) mutual eigenbasis are uncorrelated. Then such a basis is separable.]
Sometimes a mutual eigenbasis exhibit _some_ tensor product structure. For
example, for hydrogen atom gross structure or 3D harmonic oscillator model, we
have mutual eigenbasis labeled as $ket((E, l, m))$#footnote[As later shown, $E$ is the eigenvalue for Hamiltonian (energy), $l,m$ are used
to label eigenvalues for $op(L^2), op(L)_z$.] where $E,m$ are only related
through $l$. So we may re-identify our space and write such basis as $ket((E,l)) tp ket((l,m))$,
but this basis is not the same as "${ket((E,l))} tp {ket((l,m))}$".
= Basic Dynamics
== Position Operator
Quantum theory is not building everything from ground up. The @postulates we
have is more about mathematical framework of the theory but tells nothing about
the _physics_ of quantum mechanics.
As for physics, we don't forgo the classical description of space-time. In fact
we will be working with non-relativistic space-time in this note. That means, we "postulate"
(this is in principle experimentally verifiable).
#def[Coordinate (Position) Operators][
There exists operators $op(x), op(y), op(z)$ on $L^2(RR^3)$#footnote[This is of course mathematically wrong. "$delta$-function" don't live in $L^2(RR^3)$.
But we will forgive this notation as we don't care about these issues in this
note.]. Defined as
$ (op(x) f)(x, y, z) = x f(x,y,z) $
And similarly for the others. From definition, they are mutually commutative.
The eigenvalues of these operators are continuous, and eigenvectors are $ket(x_0) = delta(x - x_0)$.
This is exemplified as for any test function $f$,
$ al f, x delta(x - x_0) ar = x_0 f(x_0) = x_0 al f, delta(x-x_0) ar $
Thus we identify $op(x) delta(x - x_0) = x delta(x-x_0) = x_0 delta(x-x_0)$.
By mutual commutativity, they have a mutual eigenbasis defined as $ket(vb(x_0)) = delta(vb(x) - vb(x)_0)$.
Or equivalently $delta(x - x_0) delta(y - y_0) delta(z - z_0)$ which sort of
shows the separable nature of their mutual eigenbasis.
As a convention, $ket(vb(x_0))$ where $vb(x_0)$ is a real vector, means a
position eigenstate with eigenvalue $vb(x_0)$.
]
#warning[
As you might already know, these eigenvectors are not square-integratable. That
is to say using integral, we cannot get $braket(x_0, x_0) = 1$. As
$ braket(x_0, x_1) = integral_(RR^3) delta(x - x_0) delta(x - x_1) $
is not well-defined.
The only thing we can "say" is to understand $braket(x_0, x_1) = delta(x_0 - x_1)$.
]
In the above, we think of vectors are functions in $L^2(RR^3)$ but
alternatively, we can also think vector $ket(phi)$ lives in some other space.
And $phi(vb(x)_0)$ as the "coordinate" for $ket(phi)$ obtained using $braket(vb(x_0), phi)$.
In this way, $braket(vb(x_0), vb(x_1)) = delta(vb(x_0) - vb(x_1))$ then gives
the coordinate for eigenvectors $ket(vb(x_1))$.
Position operators are the easiest example of a vector operator.
#def[Vector Operator][
Given three#footnote[Of course you may go to higher dimension. Generalization will require us to
think about 4D angular momentum and rotation.] operators $op(v)_1, op(v)_2, op(v)_3$,
we can apply them together on some state $ket(phi)$ and get a triplet of vector:
$ (op(v)_1 ket(phi), op(v)_2 ket(phi), op(v)_3 ket(phi)) in cal(H)^3 $
Or written succinctly as
$ vecop(v) ket(phi):= (op(v)_1 ket(phi), op(v)_2 ket(phi), op(v)_3 ket(phi)) $
*Criterion*: We call $vecop(v)$ or the triplet $(op(v)_1, op(v)_2, op(v)_3)$ as
vector operator if we expect physically their measurements are component of some
vector. This implies they must change collectively under rotation, inversion
etc. And more is discussed on this later.
]<vecop>
#def[Notation Shorthands for Vector Operators][
- *Dot Product*: Vector operator can be defined to take "dot product", which is
just defined as
$ vecop(v) cdot vecop(v) := op(v)_1 compose op(v)_1 + op(v)_2 compose op(v)_2 + op(v)_3 compose op(v)_3 $
- *Eigenvalue*: _If_ the operators of each component (i.e. $op(v)_i$) of $vecop(v)$ are
mutually commutative, we have simultaneous eigenspaces for all components. And
thus we could write a vector eigenvalue:
$ vecop(v) ket(vb(a)) = vb(a) ket(vb(a)) := (a_1 ket(vb(a)), a_2 ket(vb(a)), a_3 ket(vb(a))) $
- *Rotation*: Let $R: RR^3 to RR^3$ be a 3D rotational matrix, we could define $R vecop(v)$,
the vector operator after rotation as
$ (R vecop(v))_i = sum_j R_(i,j) vecop(v)_j $
]<shorthands-vecop>
#warning[
Despite the fact that the components of $vecop(x)$ (and as we see later $vecop(p)$)
are mutually commutative, it's not true in general that a vector operator has
commutative components. An important example is angular momentum where it's
components satisfy
$ [op(J)_i, op(J)_j ] = ii epsilon_(i,j,k) op(J)_k $
where we used Einstein summation (and we will for the rest of note).
And a particular consequence of this is it's illegal to write $ket(vb(J))$, an
angular momentum eigenket with well-defined components for all three directions.
]
Since we expect position operators $op(x), op(y), op(z)$ to physically mean the
components of a vector, they form a vector operator. And we write it as $vecop(x)$ or $vecop(r)$.
We can define new operators using some $f: RR^3 to RR$.
#def[Function of Position Operator][
Given suitable $f: RR^3 to RR$, we define $f(vecop(x)): L^2(RR^3) to L^2(RR^3)$ as
$ (f(vecop(x)) phi)(vb(x)) := f(vb(x)) phi(vb(x)) $
Of course $f$ has to be suitable in order for the resultant vector to still be
square-integrable.
]
#eg[Electrostatic Potential][
Electrostatic potential classically is defined as $V(vb(r)) = 1/(4 pi epsilon_0) Q/(|vb(r)|)$.
Quantum mechanically, we _guess_ the corresponding operator to be $V(vecop(x))$.
Notice it's hard to define what $sqrt(op(x)^2 + op(y)^2 + op(z)^2)$ as $sqrt(1+x^2)$'s
Taylor series would only converge over a finite domain of convergence.
]
== Momentum Operator
#tip[$hbar$ is in unit of angular momentum. And it's a natural unit of angular
momentum eigenvalue.]
Up till now, we cannot give a motivation for momentum operator other than just
simply define it. We will have some more understanding once we introduced
transformation.
#def[Momentum Operator][
Momentum is also a vector operator as we expect the measurement outcome to be
components of some "momentum vector".
Denote the triplet as $op(p)_i: L^2(RR^3) to L^2(RR^3)$ where $i = x,y,z$ which
means measurement of $x,y,z$ component of momentum. They are defined for as for $phi in L^2(RR^3)$
$ (op(p)_i phi)(vb(x)) = - ii hbar pdv(phi, x_i) $
As partial derivative commutes, $op(p)_i$ are mutually commutative.
Note in the "other perspective" where $phi(vb(x))$ are seen as coordinate
instead of state itself, $(op(p)_i phi)(vb(x)) = bra(vb(x)) op(p)_i ket(phi)$.
We will use both perspective as we go on. Written in that perspective, $op(p)_i$ is
defined by
$ bra(vb(x)) op(p)_i ket(phi) = - ii hbar pdv(braket(vb(x), phi), x_i) $
]
It can be verified directly that
$ [op(p)_i, op(x)_j] = -ii hbar delta_(i,j) $
Up till now, we see#footnote[By in principle carrying out the procedure in @csco-procedure.] a
possible CSCO (if we only work on spinless dynamics) is the position operator
triplet. And the Hilbert space we work with is $L^2(RR^3)$.
The eigenvector of $op(p)_i$ can be found by solving the definition equation.
Because $op(p)_i$ are mutually commutative, we may actually find an eigenvector
for the collective $vecop(p)$.
Let $ket(vb(p))$ be the eigenvector of $vecop(p)$ with eigenvalue $vb(p)$ (see
@shorthands-vecop), we then have
$ bra(vb(x)) op(p)_i ket(vb(p)) = - ii hbar pdv(braket(vb(x), vb(p)), x_i) = vb(p)_i braket(vb(x), vb(p)) $
for all $i=x,y,z$.
And $ braket(vb(x), vb(p)) = exp(ii vb(p) cdot vb(x) /hbar) $
Again, it's not normalizable. However, we could demand a normalization similar
to $braket(vb(x), vb(x'))$, so we want
$ braket(vb(p), vb(p')) = delta(vb(p) - vb(p')) $
But $ integral_(RR^3) exp(-ii vb(p) cdot vb(x) /hbar) exp(ii vb(p') cdot vb(x) /hbar) dd(vb(x), 3) &= hbar^3 integral_(RR^3) exp(-ii vb(p) cdot vb(x) /hbar) exp(ii vb(p') cdot vb(x) /hbar) dd(vb(x)/hbar, 3) \
&= hbar^3 ft(exp(ii vb(p') cdot vb(u)), vb(p)) $
where $vb(u) = vb(x) / hbar$. Notice
$ integral_(RR^3) exp(ii vb(p) cdot vb(u)) delta(vb(p) - vb(p')) dd(vb(p), 3) &= exp(ii vb(p') cdot vb(u)) \
&= (2pi)^3 invft(delta(vb(p)- vb(p')), vb(u)) $
So
$ hbar^3 ft(exp(ii vb(p') cdot vb(u)), vb(p)) &= (2pi hbar)^3 ft(invft(delta(vb(p)- vb(p')), vb(u)), vb(p)) \
&= (h)^3 delta(vb(p)- vb(p')) $
As $hbar:= h / (2pi)$. Therefore, we have could normalize
$ ket(vb(p)) := h^(-3/2) exp(ii vb(p) cdot vb(x) / hbar) $
== Uncertainty Principle
For two non-commutative operators, we have a nice inequality
#thm[(Heisenberg) Uncertainty Principle][
Let $op(P), op(Q)$ be two general Hermitian operator. Define $op(p) = op(P) - a, op(q) = op(Q) - b$ where $a,b in RR$.
Then, for a state $ket(phi)$,
$ sqrt(expval(op(p)^2) expval(op(q)^2)) gt.eq 1/2 |expval([op(P),op(Q)])| $
In particular, if $a = expval(op(p)), b = expval(op(Q))$ then $expval(op(p)^2) = expval(op(P)^2)- expval(op(P))^2$ is
the variance $(Delta P)^2$ of $op(P)$. Similar for $expval(op(q)^2)$. This then
means
$ (Delta P) (Delta Q) gt.eq 1/2 |expval([op(P), op(Q)])| $
And further, for $op(P) = op(p)_i, op(Q) = op(x)_j$,
$ (Delta p_i) (Delta x_j) gt.eq 1/2 delta_(i,j) hbar $
]<heisenberg-inequality>
#proof[
#pfstep[$op(p), op(q)$ are Hermitian as well.][
Since $a,b in RR$, $ op(p)^dagger = op(P)^dagger - a = op(P) - a = op(p) $
Similar for $op(q)$.
]
#pfstep(
finished: true,
)[$[op(P), op(Q)] = [op(p), op(q)]$][
$ [op(p), op(q)] = [op(P) - a, op(Q) - b] &= [op(P), op(Q)-b] - underbrace([a, op(Q) - b], "trivially 0") \
&= [op(P), op(Q) ] - underbrace([op(P), b], "trivially 0") \
&= [op(P), op(Q) ] $
]
Now, since $op(p), op(q)$ are Hermitian,
$ expval(op(p)^2)expval(op(q)^2) &= expval(op(p)^dagger op(p)) expval(op(q)^dagger op(q)) \
&= norm(op(p) ket(phi))^2 norm(op(q) ket(phi))^2 $
And by Cauchy-Schwartz
$ norm(op(p) ket(phi)) norm(op(q) ket(phi)) gt.eq |expval(op(p)op(q), phi)| $ <c-s-uncertainty-1>
And
$ norm(op(p) ket(phi)) norm(op(q) ket(phi)) gt.eq |expval(op(q)op(p), phi)| $ <c-s-uncertainty-2>
Adding @c-s-uncertainty-1 and @c-s-uncertainty-2, and use triangular inequality
$ 2 norm(op(p) ket(phi)) norm(op(q) ket(phi)) >.eq |expval(op(q)op(p), phi)| + |expval(-op(q)op(p), phi)| \
>.eq |expval([op(p), op(q)], phi)| = |expval([op(P), op(Q)], phi)| $
Thus $ norm(op(p) ket(phi)) norm(op(q) ket(phi)) gt.eq 1/2 |expval([op(p), op(q)], phi)| $
]
The specialization of @heisenberg-inequality applied to $op(x), op(p)$ is
actually also interpreted as inequality on Fourier Transform.
Specifically, when we work in 1D, let $op(p)$ represent momentum operator again
(but without $hbar$),
$ braket(p, phi) = integral_RR exp(ii p x) phi(x) dd(x) = ft(phi(x), p) $
And $ expval((op(p) - a)^2, phi) &= integral_RR mel(phi, (op(p)- a)^2, p) braket(p, phi) dd(p) \
&= integral_RR (p- a)^2 braket(phi, p) braket(p, phi) dd(p) \
&= integral_RR (p- a)^2 |ft(phi(x), p)|^2 dd(p) $
So the @heisenberg-inequality is then about the variance of $phi(x)$ and its
Fourier transform.
== Time Evolution and Some Theorems
#def[Schrödinger Equation][
Let $ket(phi(t)): RR to cal(H)$ describes the trajectory of some system with
Hamiltonian $op(H)$, then
$ ii hbar pdv(ket(phi(t)), t) = op(H) ket(phi(t)) $
]<schroedinger-eqn>
#remark[
It's sometimes confusing when we deal with derivative. A few points to make
- Since $ket(phi(t))$ is _only_ a function of $t$, it can only be differentiated
with respect to $t$. The _partial_ derivative appear more because of a
conventional reason. That is, we often work with position representation $phi(vb(x), t) := braket(vb(x), phi(t))$.
So a partial derivative is necessary.
- It can be verified that $(pdv(, x))^+ = - pdv(, x)$ _in Cartesian coordinate_#footnote[It's also *wrong* to naively assume this anti-Hermitian property holds in other
coordinate system (e.g. spherical coordinates). See @binney[Exercise 7.14] for
an example.]. However, it's *wrong* to write
$ (pdv(phi(vb(x), t), x_i))^+ = -phi(vb(x), t) pdv(, x_i) $
Written clearly, we actually have $D_x$ defined as $mel(x, D_x, phi) = pdv(braket(x, phi), x)$.
And to find $(D_x ket(phi))^dagger in cal(H)'$, we act it on arbitrary $ket(psi)$,
that is
$ (D_x ket(phi))^dagger ket(psi) = mel(phi, D_x^dagger, psi) $
And $ mel(phi, D_x^dagger, psi) &= integral_RR dd(x) mel(phi, D_x^dagger, x) braket(x, psi) \
&= integral_RR dd(x) overline(mel(x, D_x, phi)) psi(x) \
&= integral_RR dd(x) pdv(overline(phi(x)), x) psi(x) \
&= cancel(eval(phi(x)psi(x))_(-oo)^(oo)) - integral_RR dd(x) overline(phi(x)) pdv(psi(x), x) $
So the correct adjoint has no simple form but $-integral_RR compose overline(phi) compose pdv(, x)$.
- The Hilbert Space $cal(H)$ is not defined to include $t$#footnote[Otherwise we are implying state to vanish at distant past and future.].
Scalar product is always taken at fixed $t$. So it *makes no sense* to write
$ (pdv(, t))^+ $
And adjoint on $cal(H)$ commutes with $pdv(, t)$ as basically $t$ has nothing to
do with $cal(H)$. Thus,
$ (pdv(ket(phi(t)), t))^+ = pdv(bra(phi(t)), t) $
]<time-derivative-remark>
#thm[Time-evolution of energy eigenstate][
Let $ket(phi_0)$ be an eigenstate of $op(H)$ with eigenvalue $E$. Let $ket(phi(0)) = ket(phi_0)$,
we have
$ ket(phi(t)) = exp(-ii E t/hbar) ket(phi(0)) $
]<time-evolution-of-energy-eigenstate>
#proof[
Plug in @schroedinger-eqn, we have
$ pdv(ket(phi(t)), t) &= -ii / hbar E ket(phi(t)) \
ket(phi(t)) &= exp(- ii E t /hbar) ket(phi(0)) $
assuming we have defined norms etc in $cal(H)$ so differentiating $ket(phi(t)): RR to cal(H)$ is
valid.
]
#remark[This means the eigenvector of $op(H)$ changes only phases over time. *And it
stays as an eigenvector of $op(H)$!*]
#thm[Ehrenfest Theorem][
Ehrenfest Theorem states the time evolution of _expectation value_ of some
operator under certain Hamiltonian. For time-independent operator $op(Q)$,
$ ii hbar dv(expval(op(Q), phi(t)), t) = expval([op(Q), op(H)]) $
]<ehrenfest-theorem>
#proof[
By taking adjoint on @schroedinger-eqn, we have
$ -ii hbar pdv(bra(phi(t)), t) = bra(phi(t)) op(H) $
And $ ii hbar dv(expval(op(Q), phi(t)), t) &= (ii hbar pdv(bra(phi(t)), t)) op(Q) ket(phi) + bra(phi) op(Q) (ii hbar pdv(ket(phi(t)), t)) \
&= - expval(op(H)op(Q), phi) + expval(op(Q)op(H), phi) = expval([op(Q), op(H)]) $
where we assumed $op(Q)$ is time-independent.
]
#remark[Heisenberg's picture would give a similar statement.]
We haven't said anything about how to construct Hamiltonian. The answer, at
least at our stages, is to "guess" based on classical mechanics. So we think of
Hamiltonian as "energy" and for example write kinetic energy as $vecop(p)^2/(2m)$ where $vecop(p)^2 equiv vecop(p) cdot vecop(p)$.
#thm[Energy Eigenstates give stationary value for all operators][
Given an arbitrary energy eigenstate $ket(E)$, we get $expval(op(Q), E)$ stationary
over time for all $op(Q)$.
]
#proof[
By @time-evolution-of-energy-eigenstate, energy eigenstate only evolves their
phases.#footnote[$ket(E(t))$ means the evolution of $ket(E)$, not meaning the eigenvalue $E$ is
changing over time.]
$ ket(E(t)) = exp(-ii E t/hbar) ket(E(0)) $
So $ expval(op(Q), E(t)) = exp(-ii(E-E) t/hbar) expval(op(Q), E(0)) = expval(op(Q), E(0)) $
Alternatively, we can use @ehrenfest-theorem by plugging in $expval([op(Q), op(H)], E(t))$
]
#thm[Virial Theorem][See Binney]
== Probability Current
Consider now the special case when we are studying position and momentum so $cal(H) = L^2(RR^3)$.
We have actually been implicitly assuming the interpretation that amplitude
squared, $|phi(vb(x), t)|^2$, serves as the probability (density) function. And
it's then natural to ask how probability shifts over time. This is also
important for us to study 1D scattering problems (e.g. potential well problems)
by giving interpretation about transmission and reflection.
We further assume our Hamiltonian is simply#footnote[More complicated Hamiltonian will admit different probability current. For
example, Hamiltonian with a classical electromagnetic field will have a
probability current that transforms under gauge transformation correctly.]
$ op(H) = vecop(p)^2 / (2m) + V(vecop(x)) $
#thm[Probability Current For Simple System][
Let $ket(phi(t)) = |phi(vb(x), t)| exp(ii theta(vb(x), t))$ be a state, define $rho(vb(x), t) = |phi(vb(x), t)|^2$.
We have
$ pdv(rho, t) = - div vb(J) $
where $vb(J) = hbar / m rho grad theta $.
]
#proof[
By definition, $rho = braket(phi, vb(x)) braket(vb(x), phi)$. And by
@schroedinger-eqn,
$ ii hbar pdv(braket(vb(x), phi), t) &= mel(vb(x), op(H), phi) \
- ii hbar pdv(braket(phi, vb(x)), t) &= mel(phi, op(H), vb(x)) $
By product rule,
$ ii hbar pdv(rho, t) &= ii hbar pdv(braket(vb(x), phi), t) braket(phi, vb(x)) + ii hbar pdv(braket(phi, vb(x)), t) braket(vb(x), phi) \
&= mel(vb(x), op(H), phi) braket(phi, vb(x)) - mel(phi, op(H), vb(x)) braket(vb(x), phi) \
&= 2ii Im mel(vb(x), op(H), phi) braket(phi, vb(x)) $
And $ mel(vb(x), op(H), phi) braket(phi, vb(x)) = - hbar^2 / (2m) (laplacian phi) conj(phi) + V(vb(x)) rho $
Since the second term is real,
$ ii hbar pdv(rho, t) = - hbar^2 / (m) ii Im (laplacian phi) conj(phi) \
pdv(rho, t) = - hbar / m Im (laplacian phi) conj(phi) $
Notice, $(laplacian phi) conj(phi) = (div grad phi) conj(phi)$, and $div (psi vb(F)) = vb(F) cdot grad(psi) + psi div vb(F)$.
Set $vb(F) = grad phi, psi = conj(phi)$, we have
$ Im (laplacian phi) conj(phi) = div(Im conj(phi) grad phi) - underbrace(grad phi cdot grad conj(phi), in RR) $
So we could identify $ vb(J) = hbar / m Im conj(phi) grad phi $
And let $phi = |phi| exp(i theta)$,
$ Im conj(phi) grad phi &= Im |phi| exp(-i theta) ((grad |phi|) exp(i theta) + |phi| i (grad theta ) exp(i theta)) \
&= Im underbrace(|phi| grad |phi|, in RR) + i |phi|^2 grad theta \
&= rho grad theta $
Thus $vb(J) = hbar / m rho grad theta$
]
#remark[
Since the particle has to be found somewhere in $RR^3$, surface integral with $vb(J)$ allows
us to work out how fast a particle moves out/in a particular region.
This is useful in analyzing 1D potential barrier problems. As for those problems
we have unnormalizable eigenstates, so we have to work with the rate of
particle's movement.
]
#pagebreak()
= Transformation and Symmetry
When we think of transformation, they actually form a group. That means there
exists a set of transformation $G$ and $compose: G times G to G$ that applies
one transformation after another. And they satisfy
1. $G$ is closed under $compose$.
2. $compose$ is associative.
3. There exists a transformation $e in G$ that does nothing: $e compose g = g$ for
all $g in G$.
4. For every $g in G$, there exists $inv(g) in G$ such that $inv(g) compose g = e$.
These axioms are quite naturally required when we talk about any transformation
(e.g. rotation, reflection) for some physical system. And this chapter is to
basically find "representation" of these group elements $g$ as operators on the
Hilbert $cal(H)$. We denote the representation of $g$ as $op(U)(g): cal(H) to cal(H)$.
After some transformation, the probability for any measurement should remain the
same. This is particularly evident for coordinate transformation: any physics
should not be changed when we change coordinates. That is,
$ |braket(phi, psi)| = |mel(phi, op(U)^+(g) op(U)(g), psi)| $
Wigner's theorem says
#thm[Wigner's theorem][
Any operator $op(U)$ such that
$ |braket(phi, psi)| = |mel(phi, op(U)^+ op(U), psi)| $
is either
- Linear and unitary:
$ op(U)(a ket(phi) + b ket(psi)) &= a op(U) ket(phi) + b op(U) ket(psi) \
mel(phi, op(U)^+ op(U), psi) &= braket(phi, psi) $
or
- Anti-linear and anti-unitary:
$ op(U)(a ket(phi) + b ket(psi)) &= conj(a) op(U) ket(phi) + conj(b) op(U) ket(psi) \
mel(phi, op(U)^+ op(U), psi) &= braket(psi, phi) $
]
We will not prove Wigner's theorem. And we will consider our representation as
unitary and linear (i.e. ignore the other possibility).
Now, naturally we should have
$ op(U)(g_1 compose g_2) equiv op(U)(g_1) op(U)(g_2) $
So these two operators differ by a phase when acting on different states. That
is
$ op(U)(g_1 compose g_2) ket(phi) = exp(ii theta(g_1, g_2, ket(phi))) op(U)(g_1) op(U)(g_2) ket(phi) $
It can be proven @babis[Pg. 120] that this phase doesn't depend on $ket(phi)$,
and we can do some trick to get rid of the phase, that is to get representation
such that
$ op(U)(g_1 compose g_2) = op(U)(g_1) op(U)(g_2) $
== Schro\u{308}dinger and Heisenberg Pictures
When we transform states $ket(phi) to op(U) ket(phi) = ket(phi')$, it is said we
are using Schro\u{308}dinger picture. Transformation can also alternatively be
viewed as acting on the operators. That is for all $ket(phi)$,
$ expval(op(Q), phi') = expval(op(U)^+ op(Q) op(U), phi) $
So we can define $ op(Q)' := op(U)^+ op(Q) op(U) $ and transform operators
instead of states. This is the Heisenberg Picture.
== Continuous Transformation
Some transformation (e.g. rotation, displacement) can have uncountable elements,
parameterized by some parameter $theta_a, a = 1, 2, 3, dots, N$.
When $theta_a = 0$ for all $a$, we set $g(theta_a) = e$. This also naturally
gives $op(U)(g(0)) = II$.
We assume#footnote[This should be able to made rigorous, but that involves quite amount of math.
Better just take a leap of faith.] that their representation is differentiable
with respect of parameters. That is, if the group is parameterized by a single
continuous parameter $a$, then
$ eval(dv(op(U)(g(a)), a))_(a=0) =: -ii op(T) op(U)(g(0)) = -ii op(T) $
Here $-ii$ is taken by convention. $op(T)$ is called the generator.
#def[Generator][
Let $g(theta_a)$ be parameterized by $theta_a, a = 1,2,3,dots, N$. Then define
generator $op(T)_a$ as
$ eval(pdv(op(U)(g(theta_a)), theta_a))_(theta_a = 0, forall a) =: -ii op(T)_a $
]
#thm[Generator is Hermitian]<generator-is-hermitian>
#proof[
Since $op(U)$ is unitary, $ eval(pdv(op(U)^+ op(U), theta_a))_(theta_a = 0, forall a) = eval(pdv(II, theta_a))_(theta_a = 0, forall a) = 0 $ <eqn-generator-hermitian>
Just like differentiating state with respect to time (see
@time-derivative-remark), this differentiation on operator commutes with $dagger$,
we have
$ eval(pdv(op(U)^+, theta_a))_(theta_a = 0, forall a) =: ii op(T)_a^+ $
By product rule, @eqn-generator-hermitian gives (ommiting evaluation for
simplicity)
$ pdv(op(U)^+, theta_a) op(U) + op(U)^+ pdv(op(U), theta_a) = - ii op(T)_a + ii op(T)_a^+ = 0 $
thus $ op(T)_a = op(T)_a^+ $
]
#remark[
It follows
$ eval(pdv(op(U)^+, theta_a))_(theta_a = 0, forall a) =: ii op(T)_a $
]
If we assume $op(U)$ is nice, we can also "integrate" to get $op(U)(g(theta_a)) = exp(-i theta_a op(T)_a)$ where
we used Einstein convention so $theta_a op(T)_a equiv sum_a theta_a op(T)_a$.
=== Translation
As an easy example, consider the translation transformation. This group would be
parameterized naturally by some vector $vb(a) in RR^N$. For simplicity, we write
$ op(U)(vb(a)) := op(U)(g(vb(a))) $
*For any vector operator, we expect them to transform like an vector in
components*. Since translation in ordinary vector space would mean $v_i to v_i + a_i$,
in Heisenberg picture, we expect
$ (op(x)_i)':= op(U)^+(vb(a)) op(x)_i op(U)(vb(a)) = op(x)_i + a_i $
Let the generator of $U(vb(a))$ be $op(Gamma)_i$, we can differentiate the above
equation with respect to $a_j$ and evaluate at $vb(a) = vb(0)$ to get
$ ii op(Gamma)_j op(x)_i - ii op(x)_i op(Gamma)_j &= delta_(i,j) \
-ii [op(x)_i, op(Gamma)_j] &= delta_(i,j) \
[op(x)_i, op(Gamma)_j] &= ii delta_(i,j) $
And we may#footnote[I am skeptical that this commutator relation would completely define $op(Gamma)_j$] identify
$ op(Gamma)_j = op(p)_j / hbar $
And
$ op(U)(vb(a)) = exp(-ii a_j op(p)_j/hbar) equiv exp(-ii vb(a)/hbar cdot vecop(p)) $
At this stage, we have two "definition" of $op(p)_i$. Set $ket(phi) = U(vb(a)) ket(phi_0)$ where $ket(phi_0)$ is
a constant initial state.
$ ii hbar pdv(ket(phi), a_i) &= ii hbar (-i op(p)_i / hbar) ket(phi) = op(p)_i ket(phi) \
ii hbar pdv(braket(vb(x), phi), a_i) &= mel(vb(x), op(p)_i, phi) $<alt-momentum-def>
And
$ -ii hbar pdv(braket(vb(x), phi), x_i) = mel(vb(x), op(p)_i, phi) $
To reconcile this, notice,
$ expval(vecop(x), op(U)(vb(a)) vb(x)) = expval(op(U)^+(vb(a))vecop(x) op(U)(vb(a)), vb(x)) = expval(vecop(x) + vb(a) II, vb(x)) = vb(x) + vb(a) $
So $ op(U) (vb(a)) = ket(vb(x)+vb(a)) $
And $ mel(vb(x), op(U)(vb(a)), phi_0) = braket(op(U)^+(vb(a)) vb(x), phi_0) = braket(op(U)(-vb(a)) vb(x), phi_0) = braket(vb(x) - vb(a), phi_0) $
So @alt-momentum-def becomes
$ ii hbar pdv(braket(vb(x)-vb(a), phi_0), a_i) &= mel(vb(x), op(p)_i, phi) \
&= -ii hbar pdv(braket(vb(x)-vb(a), phi_0), x_i) \
&= -ii hbar pdv(braket(vb(x), phi), x_i) $
And these two formulation are thus equivalent.
=== Rotation Transformation
We parameterize rotation by the rotation axis vector $vb(alpha) in RR^3$. And
for any vector operator component $op(v)_i$, we _expect_
$ op(U)^+(vb(alpha)) op(v)_i op(U)(vb(alpha)) = R_(i,j) op(v)_j $<rotation-vector-op>
where $R_(i,j)$ is the rotation matrix corresponding to the axis vector $vb(alpha)$.
Remember the orthogonal matrix $R$ can be changed into a special basis
$ R = O^TT A O $
where $O$ is an orthogonal matrix that transforms $x$-axis to $hat(vb(alpha))$.
So under that basis,
$ A = mat(1, 0, 0;0, cos(alpha), -sin(alpha);0, sin(alpha), cos(alpha)) $
where $alpha = |vb(alpha)|$.
And we can differentiate $R$ with respect to $alpha$ and evaluate at $alpha = 0$,
$ dv(R, alpha) = O^TT mat(0, 0, 0;0, 0, -1;0, 1, 0) O $
And notice $ op(U)(vb(alpha)) = exp(-ii alpha hat(vb(alpha)) cdot vecop(J)) $ where $vecop(J)$ is
the generator which we will expect to be a vector operator#footnote[It turns out to be proportional to angular momentum, so it's a expected to be a
vector.].
Now, differentiate @rotation-vector-op with respect to $alpha$ and evaluate at $alpha = 0$,
$ ii [hat(vb(alpha)) cdot vecop(J), op(v)_i] = (dv(R, alpha))_(i,j) op(v)_j $
Now, set $hat(vb(alpha)) = hat(vb(x)), hat(vb(y)), hat(vb(z))$ one at a time
gives the commutation relation (just plug in and verify)
$ [op(J)_i, op(v)_j] = ii epsilon_(i,j,k) op(v)_k $<vecop-commutation-relation>
#info[
The outline of a logical derivation for angular momentum is actually:
1. Parameterize rotation group $G$ by orthogonal matrix $R(vb(alpha))$ where $vb(alpha)$ is
the rotational axis with magnitude.
2. Write
$ inv(op(U))(R(vb(beta))) op(U)(R(vb(alpha))) op(U)(R(vb(beta))) = op(U)(inv(R)(vb(beta) R(vb(alpha)) R(vb(beta)))) $
and differentiate the expression with respect to parameters $alpha_k$ to get
$ inv(op(U))(R(vb(beta))) op(J)_k op(U)(R(vb(beta))) = R(vb(beta))_(k,l) op(J)_l $<transforms-like-vector>
where $op(J)_k$ are generator corresponding to $alpha_k$. These $op(J)_k$ as we
see later is components of a vector operator $vecop(J)$.
3. Now differentiate with respect to $beta_j$ and set certain $vb(beta)$ to get the
commutation relation for $op(J)_k$.
$ [op(J)_i, op(J)_j] = ii epsilon_(i,j,k) op(J)_k $
4. @transforms-like-vector has a nice explanation due to Heisenberg picture, it's
essentially that components $op(J)_k$ of $vecop(J)$ transforms like a vector
under rotation. And we use that equation as the criterion for any tuple of
operator to be called a vector operator.
However, going to @transforms-like-vector is not really trivial#footnote[See @babis[Pg. 128, Eqn. 10.65] for a proper derivation],
we will argue physically to arrive there#footnote[Follows the route of @binney[Chapter 4]]. _However, that inverts the proper logic._
]
== Adding Electromagnetic Fields, Gauge Invariance
= Angular Momentum
For translation, the generator and observable are closely related by
$ op(U)(vb(a)) = exp(- ii 1/ hbar vb(a) cdot vecop(p)) $
And for rotation, this _turns out_ to be the same. Given the generator $vecop(J)$,
we can define angular momentum observable $hbar vecop(J)$#footnote[Remember $hbar$ is in the unit of angular momentum.].
#warning[
We use $vecop(J)$ as the rotation generator, not angular momentum operator. This
is the same as usage in @binney but different from majority of the
text/references. The advantage of such writing is to write fewer $hbar$ as we
will indeed be dealing with _generator_ for the most of the time.
However, whether observable or generator is used should be clear from
context/unit.
]
== Common Commutation Relations and Spectrum
Up until now, we have obtained nothing about $vecop(J)$ other than the
@vecop-commutation-relation. In particular, we have
$ [op(J)_i, op(J)_j] = ii epsilon_(i,j,k) op(J)_k $<Ji-Jj-commutation>
#def[Angular momentum magnitude][
Define the *angular momentum magnitude* operator $vecop(J)^2$ by
$ vecop(J)^2 := vecop(J) cdot vecop(J) equiv sum_i op(J)_i compose op(J)_i $
In three dimension this is
$ vecop(J)^2 = op(J)_x^2 + op(J)_y^2 + op(J)_z^2 $
]
$vecop(J)^2$ has some nice commutation relations.
#thm[$ [vecop(J)^2, op(J)_i] = 0 $]<J2-Ji-commutation>
#proof[
$ [vecop(J)^2, op(J)_i] &= sum_j [op(J)_j^2, op(J)_i] \
&= sum_j op(J)_j [ op(J)_j, op(J)_i ] + [ op(J)_j, op(J)_i ] op(J)_j \
&= sum_(j,k) ii epsilon_(j,i,k) (op(J)_j op(J)_k + op(J)_k op(J)_j) \
&= ii sum_(j,k) epsilon_(i,k,j) (op(J)_j op(J)_k + op(J)_k op(J)_j) \
&= ii sum_(j,k) epsilon_(i,k,j) (- op(J)_k op(J)_j + op(J)_k op(J)_j) = 0 $
]
#remark[
This wouldn't work _in general_ for other vector operators. Although it does
work for spin and orbital angular momentum as seen later.
]
@Ji-Jj-commutation and @J2-Ji-commutation gives us a nice way to work out the
spectrum of $vecop(J)^2, op(J)_k$.
Without loss of generality, we can choose $k=z$, and we have $vecop(J)^2, op(J)_z$ commuting.
By @commutative-sim-eigenspaces, we know we can label the _eigenspaces_#footnote[Not eigenstates! Since we are not sure if $vecop(J)^2, op(J)_z$ is a CSCO. In
fact it's not: orbital and spin angular momentum will also give some additional
commutation relation.] as
$ E_(beta, m) $
And let
$ ket((beta,m)) in E_(beta, m) $
denote some arbitrary eigenvector in $E_(beta, m)$ where $ vecop(J)^2 ket((beta, m)) = beta ket((beta, m)), op(J)_z ket((beta, m)) = m ket((beta, m)) $
#def[Ladder Operator][
Define ladder operators for $op(J)_z$ as
$ op(J)_pm = op(J)_x pm ii op(J)_y $
Notice
$ (op(J)_pm)^+ = op(J)_mp $
This can be similarly defined for $op(J)_x, op(J)_y$ as well,
$ op(J)_pm^x &= op(J)_y pm ii op(J)_z \
op(J)_pm^y &= op(J)_z pm ii op(J)_x $
]
#thm[Ladder Operator commutation][
$ [ op(J)_z, op(J)_pm ] &= pm op(J)_pm \
[ op(J)_+, op(J)_- ] &= 2 op(J)_z \
[ vecop(J)^2, op(J)_pm ] &= 0 $
]<J-ladder-commutation>
#proof[
$ [ op(J)_z, op(J)_pm ] &= [ op(J)_z, op(J)_x ] pm ii [ op(J)_z, op(J)_y ] \
&= ii op(J)_y pm ii (- ii ) op(J)_x \
&= pm (op(J)_x pm ii op(J)_y) = pm op(J)_pm $
Notice $ op(J)_+ op(J)_- &= op(J)_x^2 + op(J)_y^2 + ii op(J)_y op(J)_x - ii op(J)_x op(J)_y \
&= op(J)_x^2 + op(J)_y^2 + ii [ op(J)_y, op(J)_x ] \
&= op(J)_x^2 + op(J)_y^2 + op(J)_z $
And similarly, $ op(J)_- op(J)_+ = op(J)_x^2 + op(J)_y^2 - op(J)_z $
Thus,
$ [ op(J)_+, op(J)_- ] &= 2 op(J)_z $
And $ [ vecop(J)^2, op(J)_+ ] &= [ op(J)_+ op(J)_- - op(J)_z + op(J)_z^2, op(J)_+ ] \
&= - 2 op(J)_+ op(J)_z - [op(J)_z, op(J)_+] + {[op(J)_z, op(J)_+], op(J)_z} \
&= - 2 op(J)_+ op(J)_z - [op(J)_z, op(J)_+] + {op(J)_+, op(J)_z} \
&= - {op(J)_+, op(J)_z} + {op(J)_+, op(J)_z} = 0 $
Similarly, $[ vecop(J)^2, op(J)_- ] = 0$.
]
Let $ket((beta, m))$ be an eigenvector in the eigenspace $E_(beta, m)$.
@J-ladder-commutation gives,
$ op(J)_z op(J)_pm ket((beta, m)) &= ([op(J)_z, op(J)_pm] + op(J)_pm op(J)_z) ket((beta, m)) \
&= (pm op(J)_pm + op(J)_pm op(J)_z ) ket((beta, m)) \
&= op(J)_pm (pm II + op(J)_z) ket((beta, m)) \
&= (m pm 1) op(J)_pm ket((beta, m)) $
Thus as long as $op(J)_pm ket((beta, m)) eq.not 0 $, it's in eigenspace $E_(beta, m pm 1)$.
Here $beta$ doesn't change since $[vecop(J)^2, op(J)_pm] = 0$.
The case when $op(J)_pm ket((beta, m)) = 0 $ is very important. In fact, it must
happen.
#thm[Spectrum of $vecop(J)^2, op(J)_z$][
The spectrum is such that
$ 0 lt.eq beta = m_0 (m_0 + 1), 0 lt.eq m_0 in NN/2 $
And
$ ker op(J)_+ = E_(beta, m_0), ker op(J)_- = E_(beta, m_1) $
where $m_1 = - m_0$
]<angular-momentum-spectrum>
#proof[
#pfstep[$beta gt.eq 0$][
$ beta &= expval(vecop(J)^2, (beta, m)) = expval(op(J)_x^2 + op(J)_y^2 + op(J)_z^2, (beta, m)) \
&= norm(op(J)_x ket((beta, m)))^2 + norm(op(J)_y ket((beta, m)))^2 + norm(op(J)_z ket((beta, m)))^2 gt.eq 0 $<beta-positive>
]
#pfstep[$beta = m_0(m_0 + 1)$ for some $m_0$, and $op(J)_+ E_(beta, m_0)= {0}$.][
$ norm(op(J)_+ ket((beta, m)))^2 &= expval(J_- J_+, (beta,m)) \
&= expval(vecop(J)^2 - op(J)_z^2 - op(J)_z, (beta, m)) \
&= beta - m^2 - m gt.eq 0 $ <J-plus-bound>
#pfstep[$op(J)_+ E_(beta, m_0) = {0}$ for some $m_0$][
We must first have a non-trivial eigenspace $E_(beta, m') eq.not {0}$ otherwise
all statements are vacuous.
Suppose $op(J)_+ ket((beta, m)) eq.not 0$ for all $m$. Then we can keep apply $op(J)_+$ to $ket((beta, m'))$ to
generate $ket((beta, m))$ for arbitrarily large $m$. Since $m^2 + m$ is
unbounded, this means @J-plus-bound is violated.
Thus $op(J)_+$ must annihilates $ket((beta, m_0)) eq.not 0$ for some $m_0$.
Later we will see such $m_0$ is unique.
]
Such annihilation would require $ norm(op(J)_+ ket((beta, m_0)))^2 = beta - m_0(m_0 + 1) = 0 $
]
#pfstep[$beta = m_1(m_1 - 1)$ for some $m_1$, and $op(J)_- E_(beta, m_1) = {0}$.][
Similar to above,
$ norm(op(J)_- ket((beta, m)))^2 &= expval(J_+ J_-, (beta,m)) \
&= expval(vecop(J)^2 - op(J)_z^2 + op(J)_z, (beta, m)) \
&= beta - m^2 + m gt.eq 0 $
And there must some $m_1$ such that
$ norm(op(J)_- ket((beta, m_1)))^2 = beta - m_1(m_1 - 1) = 0 $
]
#pfstep[$m_1 = -m_0, m_0 gt.eq 0$ and $m_0, m_1$ are unique given $beta$.][
#pfstep[$m_1 = -m_0$][
$ m_0(m_0+1) = beta = m_1 (m_1 - 1) $
We can solve $m_1$ in terms of $m_0$ to get $m_1 = -m_0$ or $m_1 = m_0 + 1$. The
latter case is impossible. This is because we can solve separately for $m_0, m_1$ in
terms of $beta$ to get
$ m_0 = (-1 pm sqrt(1 + 4 beta)) / 2, m_1 = (1 pm sqrt(1 + 4 beta)) / 2 $
And in order for $m_0 +1 = m_1$ we must have
$ sqrt(1+4beta) &= 1 - sqrt(1 + 4beta) \
beta &= -3/16 < 0 $
which contradicts with @beta-positive. Therefore, $m_0 = -m_1$.
]
#pfstep[$m_0 gt.eq 0$ and $m_0, m_1$ are unique given $beta$][This gives two pairs of solutions
$ cases(
m_0 = (-1 + sqrt(1 + 4 beta)) / 2 gt.eq 0, m_1 = (1 - sqrt(1 + 4 beta)) / 2,
) "or" cases(
m_0 = (-1 - sqrt(1 + 4 beta)) / 2 < 0, m_1 = (1 + sqrt(1 + 4 beta)) / 2,
) $<m0-m1-cases>
Suppose $m_0< 0$, then we know $E_(beta, m_0 - 1) eq.not emptyset$ because we
can obtain one#footnote[As $m_1 eq.not m_0$, otherwise $m_1 = m_0 = 0$ and we automatically excluded $m_0 < 0$ case.] by $op(J)_- ket((beta, m_0))$.
And this means we can act $op(J)_+$ on some $ket((beta, m_0 - 1))$,
$ norm(op(J)_+ ket((beta, m_0 - 1)))^2 = beta - (m_0 - 1)^2 - m_0 + 1 = 2m_0 gt.eq 0 $
which contradicts with $m_0<0$. Thus only one case in @m0-m1-cases is possible,
and thus $m_0, m_1$ are unique given $beta$.]
]
#pfstep[$ker op(J)_+ = E_(beta, m_0), ker op(J)_- = E_(beta, m_1)$][
$ ket((beta, m)) in ker op(J)_+ iff norm(op(J)_+ ket((beta, m)))^2 = beta - m(m + 1) = 0 $
And we proved $beta = m_0(m_0+1)$ and $m_0$ is unique. Thus $ker op(J)_+ = E_(beta, m_0)$.
Similar for $ker op(J)_- = E_(beta, m_1)$.
]
#pfstep(
finished: true,
)[$m_0 in NN / 2$][
Starting from $E_(beta, m_1)$, applying repeatedly $op(J)_+$ must reach $E_(beta,m_0)$ as $ker op(J)_+ = E_(beta, m_0)$.
Since each time $op(J)_+$ moves $m$ to $m+1$, there exists $n in NN$ such that
$ m_1 + n = m_0 => n = 2 m_0 => m_0 = n/2 in NN / 2 $
]
]
#remark[
$m_0$ is also known as $j$ or *angular momentum magnitude quantum number*. We
will label $E_(beta=j(j+1),m)$ using $ E_(j,m) $ from now on.
]
#remark[
This theorem also tells us that $op(J)_pm$ are nil-potent on $E_(j, m)$.
]
#thm[$op(J)_pm$ moves between eigenspaces][
For $-j+1 lt.eq m lt.eq j-1$,
$ op(J)_pm E_(j, m) = E_(j, m pm 1) $
]
#proof[
For $-j lt.eq m lt.eq j-1$,
$ op(J)_+ E_(j, m) &subset.eq E_(j, m+1) \
op(J)_- E_(j, m+1) &subset.eq E_(j, m) $<J-ladder-inclusion>
And this means
$ (vecop(J)^2 - op(J)_z^2 + op(J)_z) E_(j, m+1) = op(J)_+ op(J)_- E_(j, m+1) &subset.eq op(J)_+ E_(j, m) $
But $E_(j, m+1)$ is an eigenspace of $(vecop(J)^2 - op(J)_z^2 + op(J)_z)$, so $(vecop(J)^2 - op(J)_z^2 + op(J)_z) E_(j, m+1) = E_(j, m+1)$.
Thus
$ E_(j, m+1) subset.eq op(J)_+ E_(j, m) $
And with @J-ladder-inclusion,
$ op(J)_+ E_(j, m) = E_(j, m+1) $
Similarly, one can prove, if $-j +1 lt.eq m lt.eq j$
$ op(J)_- E_(j, m) = E_(j, m-1) $
]
== Spin and Orbital Angular Momentum
== Adding Angular Momentum
== Spherical Harmonics
= Composite Systems and Identical Particles
To model system of particles, we need the following postulate.
#postl[Hilbert Space of Composite System][
Let quantum systems $A, B$ have Hilbert space $cal(H)_A, cal(H)_B$ respectively,
their collective state lives in the tensor product space
$ cal(H)_A tp cal(H)_B $
]
The idea for this postulate is rather simple: linear combination of state is
important to quantum mechanics. And if $ket(phi_1), ket(phi_2) in cal(H)_A, ket(psi_1), ket(psi_2) in cal(H)_B$,
and if systems are such that without interaction, then we should have collective
state represented $ket(phi_1) tp ket(psi_2), ket(phi_2) tp ket(psi_1)$ etc.
However, for linear combination of them to also be in the collective Hilbert
space, we will be writing
$ alpha ket(phi_1) tp ket(psi_2)+ beta ket(phi_2) tp ket(psi_1) $
which is exactly what tensor product structure allows us to do.
By the theory of tensor product, if ${ket(alpha_i)}, {ket(beta_j)}$ are basis of $cal(H)_A, cal(H)_B$ respectively, ${ket(alpha_i) tp ket(beta_j)}$ is
a basis of $cal(H)_A tp cal(H)_B$. However, it should be noticed that _eigenbasis of individual systems tensored together doesn't necessarily give an
eigenbasis of collective system's Hamiltonian_ if there are interaction betweeen
systems.
If we have three particles, we can go on and regard first two particles as a
single quantum _system_, and apply the postulate again and arrive at
$ (cal(H)_A tp cal(H)_B) tp cal(H)_C caniso cal(H)_A tp cal(H)_B tp cal(H)_C $
Since we have got Hilbert space, Schro\u{308}dinger equation and measurement
postulate generalizes.
#warning[
With Symmetrization Postulate introduced later, we cannot use the same Hermitian
operators for individual system to represent the measurement on part of the
system (e.g. on one particle of the two particle system), we have to use the
symmetrization-preserving version of them.
]
Operators that act only on part of the system like $op(S)_z^(A): cal(H)_A to cal(H)_A$ are
strictly speaking written as $op(S)_z^(A) tp II: cal(H)_A tp cal(H)_B to cal(H)_A tp cal(H)_B$.
However, for simplicity, we omit this writing.
For simplicity, we will also write product state without tensor product, that is
$ ket(phi) tp ket(psi) equiv ket(phi) ket(psi) $
== Identical and Indistinguishable Particles#footnote[Much of this section is inspired by @littlejohn[Notes 29]. I added
symmetrization of operator though.]
Sometimes, the two quantum system we consider are *identical*#footnote[We will have different meaning for "indistinguishable" and "identical".],
that is $cal(H)_A = cal(H)_B = cal(H)$.
#def[Identical System][
Two quantum systems $A,B$ are identical if $cal(H)_A = cal(H)_B$.
]<identical-system>
Now, we introduce an exchange operator $op(Pi)$.
#def[Exchange Operator][
Given two identical quantum system $A, B$, let ${ket(alpha_i)}$ be a basis for $cal(H)$ (remember $cal(H)_A =cal(H)_B$).
Define the exchange operator $op(Pi): cal(H) tp cal(H) to cal(H) tp cal(H)$ such
that
$ op(Pi) ket(alpha_i) tp ket(alpha_j) = ket(alpha_j) tp ket(alpha_i) $
for all $i,j$ and use linearity.
]
#thm[$op(Pi)$ is well defined][
The definition of $op(Pi)$ doesn't depend on basis ${ket(alpha_i)}$.
]
#proof[
Let ${ket(beta_j)}$ be another basis of $cal(H)$. Let $a_(j,i)$ be such that
$ ket(beta_j) = sum_i a_(j,i) ket(alpha_i) $
#pfstep(
finished: true,
)[$op(Pi) ket(beta_k) tp ket(beta_l) = ket(beta_l) tp ket(beta_k)$][
$ op(Pi) ket(beta_k) tp ket(beta_l) &= op(Pi) (sum_i a_(k,i) ket(alpha_i)) tp (sum_j a_(l,j) ket(alpha_j)) \
&= sum_i sum_j a_(k,i) a_(l,j) op(Pi) ket(alpha_i) tp ket(alpha_j) \
&= sum_i sum_j a_(k,i) a_(l,j) ket(alpha_j) tp ket(alpha_i) \
&= (sum_j a_(l,j) ket(alpha_j)) tp (sum_i a_(k,i) ket(alpha_i)) \
&= ket(beta_k) tp ket(beta_l) $
]
Since $op(Pi)$ is linear, definition of $op(Pi)$ using ${ket(alpha_i)}$ is
equivalent to definition using ${ket(beta_j)}$.
]
#thm[$op(Pi)^2 = II$]
#proof[By direct verification]
#thm[$op(Pi)$ is unitary]
#proof[
#pfstep(
finished: true,
)[$op(Pi)^dagger op(Pi) = II$][
We have $ (ket(alpha_j) tp ket(alpha_i))^+ = (op(Pi) ket(alpha_i) tp ket(alpha_j))^+ = bra(alpha_i) tp bra(alpha_j) op(Pi)^dagger $
And $ (bra(alpha_k) tp bra(alpha_l)) op(Pi)^dagger op(Pi) (ket(alpha_i) tp ket(alpha_j)) &= (op(Pi) ket(alpha_k) tp ket(alpha_l))^+ op(Pi) (ket(alpha_i) tp ket(alpha_j)) \
&= bra(alpha_l) tp bra(alpha_k) (ket(alpha_j) tp ket(alpha_i)) \
&= delta_(l,j) delta_(k,i) $
which means $op(Pi)^dagger op(Pi) = II$.
]
]
#def[Indistinguishable System][
Two systems are indistinguishable if they are identical _and_ their Hamiltonian
commutes with $op(Pi)$. That is
$ [op(H), op(Pi)] = 0 $
]<indistinguishable-system>
#eg[
Consider two electrons, and their Hamiltonian being
$ op(H) = vecop(p_1)^2 / (2m) + vecop(p_2)^2 / (2m) + V(|vecop(x_1) - vecop(x_2)|) $
This is indistinguishable as the Hamiltonian commutes with $op(Pi)$.
Specifically, for any product state $ket(phi_1) tp ket(phi_2)$,
$ bra(vb(a)) tp bra(vb(b)) V(|vecop(x_1) - vecop(x_2)|) op(Pi) ket(phi_1) tp ket(phi_2) &= bra(vb(a)) tp bra(vb(b)) V(|vecop(x_1) - vecop(x_2)|) ket(phi_2) tp ket(phi_1) \
&= V(|vb(a) - vb(b)|) bra(vb(a)) tp bra(vb(b)) (ket(phi_2) tp ket(phi_1)) \
&= V(|vb(a) - vb(b)|) phi_2(vb(a)) phi_1(vb(b)) $
$ bra(vb(a)) tp bra(vb(b)) op(Pi) V(|vecop(x_1) - vecop(x_2)|) ket(phi_1) tp ket(phi_2) &= bra(vb(a)) tp bra(vb(b)) op(Pi)^+ V(|vecop(x_1) - vecop(x_2)|) ket(phi_1) tp ket(phi_2) \
&= bra(vb(b)) tp bra(vb(a)) V(|vecop(x_1) - vecop(x_2)|) ket(phi_1) tp ket(phi_2) \
&= V(|vb(b) - vb(a)|) bra(vb(b)) tp bra(vb(a)) (ket(phi_1) tp ket(phi_2)) \
&= V(|vb(a) - vb(b)|) phi_2(vb(a)) phi_1(vb(b)) $
Thus the potential part commutes for basis elements in particular (use the
product basis constructed out of basis of individual system). And the kinetic
part also commutes for similar reason.
]
#eg[
Consider two electrons with Hamiltonian
$ op(H) = vecop(p_1)^2 / (2m) + vecop(p_2)^2 / (2m) + V(vecop(x_1)) + 2V(vecop(x_2)) $
This is *not* indistinguishable _despite two systems are identical (@identical-system)_ for
their individual Hilbert space.
]<identical-but-distinguishable-eg>
#eg[
Consider one spin-1 boson and one spin-$1/2$ fermion with Hamiltonian
$ op(H) = vecop(p_1)^2 / (2m) + vecop(p_2)^2 / (2m) $
This is *not* indistinguishable and Hamiltonian doesn't commute actually (*even
if it looks like so!*).
This is because bosons have integer spin while fermions have half integer spin,
and if we write out, for boson
$ cal(H)_1 = L^2(RR^3) tp CC^3 $
and for fermion
$ cal(H)_2 = L^2(RR^3) tp CC^2 $
And if we define exchange operators as before, $op(Pi): cal(H)_1 tp cal(H)_2 to cal(H)_2 tp cal(H)_1$,
And $op(H): cal(H)_1 tp cal(H)_2 to cal(H)_1 tp cal(H)_2$. So $[op(Pi), op(H)]$ doesn't
even make sense in terms of type.
]
Often it's easier to consider effect of exchange operator on other operators.
Consider $vecop(x)_1 tp II$. We have for any product state $ket(phi_1) ket(phi_2)$ and $vb(a), vb(b)$,
$ bra(vb(a)) bra(vb(b)) (vecop(x_1) tp II) compose op(Pi) (ket(phi_1) ket(phi_2)) &= bra(vb(a)) bra(vb(b)) (vecop(x_1) tp II) ket(phi_2) ket(phi_1)\
&= vb(a) phi_2(vb(a)) phi_1(vb(b)) \
&= bra(vb(a)) bra(vb(b)) op(Pi) compose (II tp vecop(x_2)) (ket(phi_1) ket(phi_2)) $
So $vecop(x_1) compose op(Pi) = op(Pi) compose vecop(x_2)$.
For a similar calculation (actually redundant),
$ bra(vb(a)) bra(vb(b)) op(Pi) compose (vecop(x_1) tp II) (ket(phi_1) ket(phi_2)) &= bra(vb(b)) bra(vb(a)) (vecop(x_1) tp II) ket(phi_1) ket(phi_2)\
&= vb(b) phi_2(vb(a)) phi_1(vb(b)) \
&= bra(vb(a)) bra(vb(b)) (II tp vecop(x_2)) compose op(Pi) (ket(phi_1) ket(phi_2)) $
So $op(Pi) compose vecop(x_1) = vecop(x_2) compose op(Pi) $.
And by $op(Pi)^2 = II$ and $op(Pi)^+ = op(Pi)$, we have
$ vecop(x_1) compose op(Pi) = op(Pi) compose vecop(x_2) implies vecop(x_1) = op(Pi)^+ compose vecop(x_2) compose op(Pi) $
That is, $vecop(x_2)$ transforms $vecop(x_1)$ under symmetrization, as expected.
Following the same argument, we have $vecop(p_1) = op(Pi)^+ compose vecop(p_2) compose op(Pi)$
Moreover, $ op(Pi)^+ vecop(p_1)_x compose vecop(p_1)_x compose op(Pi) &= vecop(p_2)_x compose op(Pi) compose op(Pi) compose vecop(p_2)_x \
&= vecop(p_2)_x compose II compose vecop(p_2)_x = vecop(p_2)_x^2 $
This means $ op(Pi)^+ vecop(p_1)^2 op(Pi) = vecop(p_2)^2 $ as we would expect.
As a rule of thumb, $op(Pi)^+ op(O) op(Pi)$ swaps the label $1,2$ in $op(O)$.
== Symmetrization Postulate
We are at the position to state the postulate
#postl[Symmetrization Postulate][
Let the total system consists of $N$ (non-composite#footnote[Saying protons or nucleus being "non-composite" is sort of wrong as they consist
of quarks. But they are fundamental enough for us. In fact _it matters little_ as
we later discuss fermionic/bosonic property of composite particles.])
particles. #underline[Any] physically realizable state of the system must be
- symmetric under exchange operator of _any indistinguishable_ pair of bosons
- anti-symmetric under exchange operator of _any indistinguishable_ pair of
fermions
And any physically realizable operators must be invariant under the $cal(H)_"phys"$,
subspace of states with correct symmetry. That is, any physical operators cannot
map physical state into unphysical state.
]<symmetrization-postulate>
#info[
This postulate is used _in reverse_ to _define_ the fermionic or bosonic
property of two indistinguishable #underline[composite] particles. More on this
later.
]
#warning[
It should be clear about what this postulate actually applies to:
indistinguishable particles.
Consider the Hamiltonian in @identical-but-distinguishable-eg, the two electrons
are distinguishable and the symmetrization postulate is empty: it says nothing
about symmetry of physical states.
]
@symmetrization-postulate makes the physical Hilbert space a subspace $cal(H)_("phys")$ of
the $cal(H)_1 tp dots.c tp cal(H)_N = cal(H)_"tot"$, and you can construct that
subspace by taking eigenstates of individual particle and tensor them up while
keeping in mind the symmetry (see also Slater determinant).
One caveats is that the postulate cannot guarantee#footnote[Simultaneous diagonalization doesn't work if we have say $N=3$ indistinguishable
particles as $[op(Pi)_12, op(Pi)_23] eq.not 0$] (at least from what literally
displayed) the existence of eigenstates of the total system with required
symmetry.
Nevertheless, it would be quite unphysical if we cannot. The reason is
Hamiltonian as a physical operator should map physical state to physical state,
which means it must be invariant under subspace $cal(H)_"phys"$, so we can write
the restriction:
$ op(H): cal(H)_"phys" subset.eq cal(H)_"tot" to cal(H)_"phys" $
Now since $op(H)$ is Hermitian in the total space, it's Hermitian in the
subspace as well, so it can be diagonalized in the subspace $cal(H)_"phys"$ and
thus admit eigenstates of correct symmetry.
We can now consider consequence of @symmetrization-postulate. For simplicity, we
will mainly discuss $N=2$ case.
== Pauli Exclusion Principle
Consider two identical and indistinguishable fermions (say electrons) under
Hamiltonian
$ op(H) = op(H)_1 + op(H)_2 $
where $op(H)_1, op(H)_2$ are actually the same except that they are acting on
different space (one for each electron). Let ${ket(phi_i)}$ be the eigenstates
of $op(H)_1, op(H)_2$, then Pauli exclusion principle is a consequence of
@symmetrization-postulate, saying
$ ket(phi_i) tp ket(phi_i) $
is not a physical state because this state is symmetric under exchange operator
of two indistinguishable _fermions_.
One natural question is then what the eigenspaces of $op(H)$ under $cal(H)_"phys"$ restriction
are. For this, let's construct the $cal(H)_"phys"$ explicitly first.
#thm[Symmetric and Anti-symmetric subspace][
Given $cal(H) tp cal(H)$ and ${ket(alpha_i)}$ being basis fo $cal(H)$, the space $cal(H) tp cal(H)$ can
be decomposed into dirac sum of two subspaces
$ epsilon_"even" := span { cases(
ket(alpha_i) tp ket(alpha_j) "if" i=j, 1/sqrt(2) (ket(alpha_i) tp ket(alpha_j) + ket(alpha_j) tp ket(alpha_i)) "if" i eq.not j,
) } $
and
$ epsilon_"odd" := span {
1/sqrt(2) (ket(alpha_i) tp ket(alpha_j) - ket(alpha_j) tp ket(alpha_i)), i eq.not j
} $
]<construction-of-symmetry-subspace>
#proof[
We can directly verify that $epsilon_"even"$ is exchange symmetric and $epsilon_"odd"$ is
anti-symmetric.
For the proof of being a basis, notice for any $i eq.not j$,
$ ket(alpha_i) tp ket(alpha_j) = 1/sqrt(2) (1/sqrt(2) (ket(alpha_i) tp ket(alpha_j) - ket(alpha_j) tp ket(alpha_i)) + 1/sqrt(2) (ket(alpha_i) tp ket(alpha_j) + ket(alpha_j) tp ket(alpha_i))) $
So these two spaces are generating, and their dimensions add up to the total
dimension.
]
With @construction-of-symmetry-subspace, we can just use the eigenstates of $op(H)_1$ as $ket(alpha_i)$.
And since we are dealing with electron (fermion), we take the $epsilon_"odd"$ as $cal(H)_"phys"$.
If the Hamiltonian commutes#footnote[Actually, on the ground of angular momentum conservation of the total system,
this must be the case.] with $op(J^2)^"tot", op(J_z)^"tot"$, then we can have
a Hamiltonian eigenbasis:
- of right symmetry
- with well defined total angular momentum magnitude and $z$ component
As $op(J^2)^"tot", op(J_z)^"tot"$ commutes with $op(Pi)$. In fact, the usual
addition of angular momentum result for spin-1/2 particles (i.e. the "triplet" "singlet")
are automatically having well-defined symmetry.
To obtain such basis, just use the textbook-style "matching spatial symmetric
with spin anti-symmetric" and "spatial anti-symmetric with spin symmetric". To
prove we indeed have a basis, observe we have the right number of linearly
independent vector.
It should be stressed that *usually system are not in states with so much
well-defined observables*. For example, consider an empty Hamiltonian and two
electrons, then
$ 1/sqrt(2) (underbrace((ket(vb(a)) tp ket(spinup)), "\"first\" electron") tp underbrace((ket(vb(b)) tp ket(spindown)), "\"second\" electron") - underbrace((ket(vb(b)) tp ket(spindown)), "\"first\" electron") tp underbrace((ket(vb(a)) tp ket(spinup)), "\"second\" electron")) $<non-entangled-state>
is a state satisfying the symmetrization postulate. I have added "first" "second"
in quote to emphasize the notion of first or second is nominal and physical
state space has symmetry between first and second.
=== Entanglement or Not? Operator Symmetrization
This state (@non-entangled-state) _seems to be_ a non-product space: we cannot
write it into the form
$ ket(phi) tp ket(psi), ket(phi) in cal(H) $
But in fact it's not an entangled state _with respect to our usual measurement_.
This again means our naive space $cal(H) tp cal(H)$ isn't really a very
favorable one as it doesn't describe our physics obviously.
The physical meaning of @non-entangled-state is quite simple: an#footnote[Notice saying _an_ electron instead of _first_ or _the_ electron is a
non-redundant description of the total system.] electron with $hbar/2$ in spin $z$ direction
at position $vb(a)$ and another electron with spin $-hbar/2$ in spin $z$ direction
at position $vb(b)$.
We _expect_, because of such simple physical interpretation, that we should be
able to measure the spin-$z$ of particle at $vb(a)$ and get a definite answer,
irrespective of how particle at $vb(b)$ behaves -- after all their physical
description look quite unentangled.
So how to measure the spin-$z$ of the particle at $vb(a)$?
For an operator to be physical, we demand it must be invariant under $cal(H)_"phys"$ by
@symmetrization-postulate. A _sufficient_ condition for this to hold is
#thm[$op(O)$ is physical if $[op(O), op(Pi)] = 0$]
#proof[
#pfstep[$op(O)$ is physical $iff$ $op(Pi) op(O) ket(phi) = lambda op(O) ket(phi)$ for
all $ket(phi) in cal(H)_"phys"$ where $lambda = plus.minus 1$ depending $cal(H)_"phys"$.][
A state $ket(phi) in cal(H)_"phys"$ if and only if
$ op(Pi) ket(phi) = plus.minus ket(phi) $
where $plus.minus$ depends on whether symmetrical or anti-symmetrical state are
physical (c.f. @symmetrization-postulate).
So for $op(O) ket(phi) in cal(H)_"phys"$,
$ op(Pi) op(O) ket(phi) = plus.minus op(O) ket(phi) $
]
#pfstep(
finished: true,
)[$[op(O), op(Pi)] = 0 implies op(Pi) op(O) ket(phi) = lambda op(O) ket(phi)$ for
all eigenvector $ket(phi)$ of $op(O)$][
$ op(Pi) op(O) ket(phi) &= op(O) op(Pi) ket(phi) \
&= lambda op(O) ket(phi) $
for any eigenvector $ket(phi)$ of $op(Pi)$.
]
]
#remark[If multiple exchange symmetry is required by @symmetrization-postulate, just
make $op(O)$ commutes with all of them.]
Clearly
$ (ketbra(vb(a), vb(a)) tp op(S_z)) tp overbrace(II, "on" cal(H)) $
doesn't work because it's not of correct symmetry. We can verify that
$ op(Pi)^+ (ketbra(vb(a), vb(a)) tp op(S_z)) tp II op(Pi) = II tp (ketbra(vb(a), vb(a)) tp op(S_z)) $
However, the operator
$ op(S_z^vb(a)) := (ketbra(vb(a), vb(a)) tp op(S_z)) tp II + II tp (ketbra(vb(a), vb(a)) tp op(S_z)) $ is
exchange symmetric. And apply it on @non-entangled-state. Part by part:
$ op(S_z^vb(a)) 1/sqrt(2) (ket(vb(a)) tp ket(spinup)) tp (ket(vb(b)) tp ket(spindown)) &= 1/sqrt(2) ((underbrace(braket(vb(a), vb(a)), 1) ket(vb(a)) tp hbar/2 ket(spinup)) tp (ket(vb(b)) tp ket(spindown)) \
& - cancel(
(ket(vb(a)) tp ket(spinup)) tp (underbrace(braket(vb(a), vb(b)), 0) ket(vb(a)) tp -hbar / 2ket(spindown))
)) \
&= hbar /2 1/sqrt(2) (ket(vb(a)) tp ket(spinup)) tp (ket(vb(b)) tp ket(spindown)) $
Similar to the other half,
$ op(S_z^vb(a)) 1/sqrt(2) (ket(vb(b)) tp ket(spindown)) tp (ket(vb(a)) tp ket(spinup)) = hbar/2 1/sqrt(2) (ket(vb(b)) tp ket(spindown)) tp (ket(vb(a)) tp ket(spinup)) $
So together @non-entangled-state is an eigenstate of $op(S_z^vb(a))$ with
eigenvalue $hbar /2$.
Notice our operator works however $vb(b)$ changes (as long as $vb(a) eq.not vb(b)$)
and the spin state of the other electron changes.
#info[
This is why electron spin measurement at lab isn't influenced by
anti-symmetrization with some other random electron light years away. Despite
@non-entangled-state looks entangled.
]
To really have some entanglement, consider the following state (also an
eigenstate of total angular momentum magnitude and component):
$ ket(Psi):= 1/2 overbrace(
(underbrace(ket(vb(a)), "1st") underbrace(ket(vb(b)), "2nd") + ket(vb(b)) ket(vb(a))), "spatial parts of two electrons",
) tp (ket(spinup) tp ket(spindown) - ket(spindown) tp ket(spinup)) $
Here I shifted position of different vectors when they get tensored together, so
product state is now in the format
$ ket("spatial of 1st") tp ket("spatial of 2nd") tp ket("spin of 1st") tp ket("spin of 2nd") $
instead of
$ ket("spatial of 1st") tp ket("spin of 1st") tp ket("spatial of 2nd") tp ket("spin of 2nd") $
If we apply $op(S_z^vb(a))$ to this state, we find at the end
$ 1/2 hbar /2 ket(vb(a)) ket(vb(b)) tp (ket(spinup) tp ket(spindown) + ket(spindown) tp ket(spinup)) &- 1/2 hbar /2 ket(vb(b)) ket(vb(a)) tp (ket(spinup) tp ket(spindown) + ket(spindown) tp ket(spinup)) \
&= 1/2 hbar /2 (ket(vb(a)) ket(vb(b)) - ket(vb(b)) ket(vb(a))) tp (ket(spinup) tp ket(spindown) + ket(spindown) tp ket(spinup)) $
So it's not an eigenstate of $op(S_z^vb(a))$.
The probability of measuring $spinup$ for the electron at $vb(a)$ is usually
given by projecting to the subspace. However, here it's not really convenient to
do this, we'd better proceed by using density operator.
We know that $ expval(op(S_z^(a))) = Tr(op(rho) op(S_z^vb(a))) $
#text(
red,
)[It's getting actually not easy at this point. Partial tracing $op(rho)$ with "first"/"second"
subspace doesn't seem to be physically meaningful to me. Partial tracing out the
position subspace of the total system doesn't give very useful information about "spin
of particle at specific location" either. Can we get to an elegant solution?]
#conclusion[
At the end of the day, all these formalism about identical particle basically
says our $cal(H)_1 tp dots.c tp cal(H)_N$ is too large. There should be a more
natural space to work with, and it's related to Fock's space and relativistic
quantum field theory.
]
== Composite Particle and Exchange Symmetry
Consider two identical and indistinguishable composite system, say two hydrogen
but _mutually not interacting_. Each hydrogen consists of one proton and one
electron where within each hydrogen the proton and electron are apparently
neither identical nor indistinguishable.
The total Hilbert space of this case is $ underbrace((cal(H)^1_e tp cal(H)^1_p), "space of hydrogen 1") tp (cal(H)^2_e tp cal(H)^2_p) $
Again "$1,2$" labeling here are nominal but not physical.
And Hamiltonian for each Hydrogen is
$ op(H)_"hydrogen" = (vecop(p)_p)^2 / (2m_p) + (vecop(p)_e)^2 / (2m_e) - 1/(4pi epsilon_0) e^2 /( |vecop(x)_p - vecop(x)_e|) $
The total Hamiltonian is two copy of $op(H)_"hydrogen"$. Clearly it's commuting
with:
- exchanging electron of hydrogen 1 with electron of hydrogen 2, denote as $op(Pi)_e$
- exchanging proton of hydrogen 1 with proton of hydrogen 2, denote as $op(Pi)_p$
Since both proton and electron are fermion, by @symmetrization-postulate, we
must have anti-symmetry on each of the above two exchanges.
*The important thing* is we can define a composite exchange that exchange two
hydrogen by performing $op(Pi)_e, op(Pi)_p$ at once. That is
$ op(Pi)_H := op(Pi)_e compose op(Pi)_p $
Clearly total Hamiltonian commutes with $op(Pi)_H$. So Hydrogen as a composite
subsystem of the total system is identical and indistinguishable according to
@indistinguishable-system.
And since any physical state $ket(phi)$ must be anti-symmetric about $op(Pi)_e, op(Pi)_p$ separately,
if we apply both, $ket(phi)$ will behave indeed symmetrically. And this means
any physical state is symmetric under $op(Pi)_H$.
By _reversing_ the @symmetrization-postulate, we _define_ Hydrogen to be a
bosonic composite particle as it behaves like a boson upon $op(Pi)_H$.
#conclusion[In general, for a composite system, we can just count the number of fermion $f$ in
the system and the particle has symmetry $(-1)^f$ and is bosonic if $f$ is even
and fermionic if $f$ is odd.]
#eg[Helium-3 is a fermionic particle][
Helium-3 has 2 protons, 1 neutron, 2 electrons, which are all fermions. So it
has fermionic exchange symmetry.
]
== Applications to Statistical Mechanics
Counting eigenstate correctly is important for statistical mechanics. We will
work through a few common examples about how exchange symmetry affect how we
count states. And in the framework of statistical mechanics, Gibbs paradox is
inherently quantum#footnote[If chambers are filled with identical particles, then the direct reason entropy
doesn't increase is increased anti-symmetry of the final eigenstates (we can
swap particles between chamber as they are indistinguishable in the final
Hamiltonian).].
=== Fermionic Harmonic Oscillator For the sake of simplicity,
Consider $N=2$ case. We are considering two spin-$1/2$ particles each
independently in a Harmonic potential. So individually the Hamiltonian is
$ op(H)_"each" = vecop(p)^2 / (2m) + 1/2 m omega^2 |vecop(x) - vb(a)|^2 $
where $vb(a)$ will be different for these two fermions as they are spatially
localized.
And we have two copy of this:
$ op(H) = op(H)_1 + op(H)_2 $
One important consequence of $vb(a)$ is that *two fermions are by definition
distinguishable!* Hamiltonian doesn't commute with exchange operator because $vb(a)$ will
be different for the two.
And in this case, we have no Pauli-exclusion whatsoever at all as
@symmetrization-postulate is empty. The whole space $cal(H)_1 tp cal(H)_2$ is
all physical.
Pauli-exclusion will take effect if two particles are in the _same_ potential
well.
=== Diatomic Gas#footnote[This example is partially studied in @littlejohn[Notes 29] as well.]
Consider a "gas" consisting of two non-interacting "molecules" each consists of
two identical spin-$1/2$ fermion. The Hilbert space of this problem is
$ underbrace((cal(H) tp cal(H)), "of a molecule") tp cal(H) tp cal(H) $
We will see despite in this problem all particles are identical, not all pairs
of particles are indistinguishable.
Each molecule has a Hamiltonian
$ op(H)_"molecule" = vecop(p_1)^2 / (2m) + vecop(p_2)^2 / (2m) + V(|vecop(x_1) -vecop(x_2)|) $
And total Hamiltonian is two copies of each molecule. Notice Hamiltonian
commutes with:
- exchanging two particles in molecule 1, denote as $op(Pi)_1$
- exchanging two particles in molecule 2, denote as $op(Pi)_2$
- exchanging two molecules, denote as $op(Pi)_m$
Commuting with $op(Pi)_m$ is ubiquitous in any ideal gas problem (this is the
origin of $N!$ in derivation of classical ideal gas partition function).
We could temporarily assume the exchange symmetry $op(Pi)_m$ doesn't exist, then
all we need to consider is eigenstates situation of each individual molecule and
multiply them together (essentially squared as they are the same). And apply
then the $N!$ approximation at the outcast.
The essential idea is we could deal with each level of symmetry individually.
Within the molecule, the symmetry is explained in more detail in
@littlejohn[Notes 29]. The result is different $l$ will give different
multiplicity#footnote[See also "spin isomer" of Hydrogen, and different multiplicity gives so-called "parahydrogen"
or "orthohydrogen".], odd $l$ state will have an additional degeneracy of $3$ and
even $l$ only has $1$. This wouldn't be the case if two particles in the
molecule are non-identical (thus distinguishable) or distinguishable in
Hamiltonian.
This affects the thermodynamic property of the molecule gas, for detail, #link(
"https://en.wikipedia.org/wiki/Spin_isomers_of_hydrogen",
)[see this Wikipedia page].
Just one thing to notice, $2l+1$ degeneracy we usually write is due to the
molecule rotation or due to $m$, whereas the degeneracy difference from exchange
symmetry is due to the spin triplet/singlet. So they are completely different,
despite all depends on $l$.
=== Gibbs Paradox
= Simple Problems and Famous Examples
== 1D Potential Problems
== 1D Harmonic Oscillators
== Central Potential Problem, 3D Harmonic Oscillator
== Hydrogen-like Atoms
= Perturbation Theory
== Time-independent Perturbation Theory
== Variation Approximation
== Sudden Limits
== Adiabatic Theorem
== Time-dependent Perturbation Theory
=== Selection Rule
#pagebreak()
#bibliography("./bib.yaml", style: "ieee")
|
https://github.com/rdboyes/resume | https://raw.githubusercontent.com/rdboyes/resume/main/modules_fr/projects.typ | typst | // Imports
#import "@preview/brilliant-cv:2.0.2": cvSection, cvEntry
#let metadata = toml("../metadata.toml")
#let cvSection = cvSection.with(metadata: metadata)
#let cvEntry = cvEntry.with(metadata: metadata)
#cvSection("Projets & Associations")
#cvEntry(
title: [Analyste de Données Bénévole],
society: [ABC Organisation à But Non Lucratif],
date: [2019 - Présent],
location: [New York, NY],
description: list(
[Analyser les données de donateurs et de collecte de fonds pour identifier les tendances et les opportunités de croissance],
[Créer des visualisations de données et des tableaux de bord pour communiquer des insights au conseil d'administration],
),
)
|
|
https://github.com/fenjalien/metro | https://raw.githubusercontent.com/fenjalien/metro/main/tests/num/bracket-ambiguous-numbers/test.typ | typst | Apache License 2.0 | #import "/src/lib.typ": num, metro-setup
#set page(width: auto, height: auto)
#num(1.2, e: 4, pm: 0.3)
#num(1.2, e: 4, pm: 0.3, bracket-ambiguous-numbers: false) |
https://github.com/storopoli/graphs-complexity | https://raw.githubusercontent.com/storopoli/graphs-complexity/main/README-pt.md | markdown | Creative Commons Zero v1.0 Universal | # Teoria dos Grafos e Complexidade Computacional
[](https://creativecommons.org/publicdomain/zero/1.0/)
[](./code/c)
[](./code/zig)
[](https://repl.it/github/storopoli/grafos-complexidade)
[](https://gitpod.io/#https://github.com/storopoli/grafos-complexidade)
> [!NOTE]
>
> For English version, please check the [README.md](README.md) file.
>
> Para a versão em inglês, por favor, confira o [README.md](README.md).
<!-- markdownlint-disable no-inline-html -->
<div class="figure" style="text-align: center">
<img src="slides/images/algorithm_analysis_meme.jpg"
alt="Algorithm meme" width="500" />
</div>
<!-- markdownlint-enable no-inline-html -->
## Conteúdo
1. Por que estudar Teoria dos Grafos e Complexidade Computacional?;
1. Grafos, Caminhos e Ciclos;
1. Árvores;
1. Complexidade Computacional;
1. Problemas P, NP-Completo, e NP-Difícil.
1. Análise de Algoritmos;
1. Algoritmos de Busca e Ordenação;
1. Recursividade;
1. Divisão e Conquista; e
1. Algoritmos Gulosos.
## Exemplos de Código
A principal linguagem de programação usada para os exemplos é C.
Também há exemplos em Zig.
Confira-os nos diretórios `code/c/` e `code/zig/`, respectivamente.
## Dependências
- Compilador C/C++;
- (Opcional) compilador [Zig](https://ziglang.org); e
- [`typst`](https://typst.app) para os slides.
Os slides são gerados usando [Typst](https://typst.app) com GitHub Actions
e podem ser encontrados na
[versão `latest`](https://github.com/storopoli/graphs-complexity/releases/latest/download/slides-pt.pdf).
## Licença
Este conteúdo é licenciado sob uma
[Creative Commons Public Domain CC0 1.0 License](https://creativecommons.org/publicdomain/zero/1.0/).
[](https://creativecommons.org/publicdomain/zero/1.0/)
|
https://github.com/typst/packages | https://raw.githubusercontent.com/typst/packages/main/packages/preview/unichar/0.1.0/ucd/block-0800.typ | typst | Apache License 2.0 | #let data = (
("SAMARITAN LETTER ALAF", "Lo", 0),
("SAMARITAN LETTER BIT", "Lo", 0),
("SAMARITAN LETTER GAMAN", "Lo", 0),
("SAMARITAN LETTER DALAT", "Lo", 0),
("SAMARITAN LETTER IY", "Lo", 0),
("SAMARITAN LETTER BAA", "Lo", 0),
("SAMARITAN LETTER ZEN", "Lo", 0),
("SAMARITAN LETTER IT", "Lo", 0),
("SAMARITAN LETTER TIT", "Lo", 0),
("SAMARITAN LETTER YUT", "Lo", 0),
("SAMARITAN LETTER KAAF", "Lo", 0),
("SAMARITAN LETTER LABAT", "Lo", 0),
("SAMARITAN LETTER MIM", "Lo", 0),
("SAMARITAN LETTER NUN", "Lo", 0),
("SAMARITAN LETTER SINGAAT", "Lo", 0),
("SAMARITAN LETTER IN", "Lo", 0),
("SAMARITAN LETTER FI", "Lo", 0),
("SAMARITAN LETTER TSAADIY", "Lo", 0),
("SAMARITAN LETTER QUF", "Lo", 0),
("SAMARITAN LETTER RISH", "Lo", 0),
("SAMARITAN LETTER SHAN", "Lo", 0),
("SAMARITAN LETTER TAAF", "Lo", 0),
("SAMARITAN MARK IN", "Mn", 230),
("SAMARITAN MARK IN-ALAF", "Mn", 230),
("SAMARITAN MARK OCCLUSION", "Mn", 230),
("SAMARITAN MARK DAGESH", "Mn", 230),
("SAMARITAN MODIFIER LETTER EPENTHETIC YUT", "Lm", 0),
("SAMARITAN MARK EPENTHETIC YUT", "Mn", 230),
("SAMARITAN VOWEL SIGN LONG E", "Mn", 230),
("SAMARITAN VOWEL SIGN E", "Mn", 230),
("SAMARITAN VOWEL SIGN OVERLONG AA", "Mn", 230),
("SAMARITAN VOWEL SIGN LONG AA", "Mn", 230),
("SAMARITAN VOWEL SIGN AA", "Mn", 230),
("SAMARITAN VOWEL SIGN OVERLONG A", "Mn", 230),
("SAMARITAN VOWEL SIGN LONG A", "Mn", 230),
("SAMARITAN VOWEL SIGN A", "Mn", 230),
("SAMARITAN MODIFIER LETTER SHORT A", "Lm", 0),
("SAMARITAN VOWEL SIGN SHORT A", "Mn", 230),
("SAMARITAN VOWEL SIGN LONG U", "Mn", 230),
("SAMARITAN VOWEL SIGN U", "Mn", 230),
("SAMARITAN MODIFIER LETTER I", "Lm", 0),
("SAMARITAN VOWEL SIGN LONG I", "Mn", 230),
("SAMARITAN VOWEL SIGN I", "Mn", 230),
("SAMARITAN VOWEL SIGN O", "Mn", 230),
("SAMARITAN VOWEL SIGN SUKUN", "Mn", 230),
("SAMARITAN MARK NEQUDAA", "Mn", 230),
(),
(),
("SAMARITAN PUNCTUATION NEQUDAA", "Po", 0),
("SAMARITAN PUNCTUATION AFSAAQ", "Po", 0),
("SAMARITAN PUNCTUATION ANGED", "Po", 0),
("SAMARITAN PUNCTUATION BAU", "Po", 0),
("SAMARITAN PUNCTUATION ATMAAU", "Po", 0),
("SAMARITAN PUNCTUATION SHIYYAALAA", "Po", 0),
("SAMARITAN ABBREVIATION MARK", "Po", 0),
("SAMARITAN PUNCTUATION MELODIC QITSA", "Po", 0),
("SAMARITAN PUNCTUATION ZIQAA", "Po", 0),
("SAMARITAN PUNCTUATION QITSA", "Po", 0),
("SAMARITAN PUNCTUATION ZAEF", "Po", 0),
("SAMARITAN PUNCTUATION TURU", "Po", 0),
("SAMARITAN PUNCTUATION ARKAANU", "Po", 0),
("SAMARITAN PUNCTUATION SOF MASHFAAT", "Po", 0),
("SAMARITAN PUNCTUATION ANNAAU", "Po", 0),
)
|
https://github.com/jneug/schule-typst | https://raw.githubusercontent.com/jneug/schule-typst/main/tests/ka/test.typ | typst | MIT License | #import "@local/schule:1.0.0": ka
#import ka: *
#import mathe: *
#show: klassenarbeit.with(
autor: (name: "<NAME>", kuerzel: "Ngb"),
titel: "2. Mathearbeit",
reihe: "Zuordnungen",
nummer: "2",
fach: "Mathematik",
kurs: "07c",
version: "2023-11-25",
variante: "A",
fontsize: 11pt,
dauer: 45,
datum: "27.11.2023",
loesungen: "seite",
)
#let vielErfolg = {
/* @typstyle:off */
let mojis = (
emoji.heart, emoji.hands.heart, emoji.arm.muscle,
emoji.heart.box, emoji.frog.face, emoji.dog.face,
emoji.monkey.face, emoji.hamster.face,
)
align(right, text(
1.4em, theme.primary, weight: "bold", font: "Comic Neue",)[
Viel Erfolg #mojis.at(calc.rem(datetime.today().day(), mojis.len()))
],)
}
#let lsg(x) = math.underline(math.underline(math.bold(x)))
#aufgabe(titel: "Rechnen mit rationalen Zahlen")[
Berechne die Lösung der Aufgaben. Rechengesetze können Dir helfen.
#unteraufgaben(cols: 2)[
- #vari[
$0,8 dot (-3) + 4,2 dot (-3)$
][
$0,6 dot (-5) + 2,4 dot (-5)$
][
$-2,3 dot 8,8 - 2,3 dot (-10,8)$
]
- #vari[
$(-20 + 21) dot (8 : (-4))$
][
$((-9) : 3) dot (45 + (-46))$
][
$(5 dot (-9)) : (-13 + 28)$
]
- #vari[
$0,25 dot 3 / 25 + (-2 / 5) dot 0,75 : 2,5$
][
$5 / 8 dot 3,5 : 1,4 + (-1,25) dot 3 / 20$
][
$0,25 dot 3 / 25 + (-2 / 5) dot 0,75 : 2,5$
]
]
#erwartung([berechnet das korrekte Ergebnis der Terme.], 9)
#loesung[
+ #vari[$
&quad 0,8 dot (-3) + 4,2 dot (-3) \
&= (0,8 + 4,2) dot (-3)\
&= 5,0 dot (-3)\
&= -15
$][$
&quad 0,6 dot (-5) + 2,4 dot (-5)\
&= (0,6 + 2,4) dot (-5)\
&= 3,0 dot (-5)\
&= -15
$][$
&quad -2,3 dot 8,8 - 2,3 dot (-10,8)\
&= -2,3 dot (8,8 - 10,8)\
&= -2,3 dot (-2)\
&= 4,6
$]
+ #vari[$
&quad (-20 + 21) dot (8 : (-4))\
&= 1 dot (-2)\
&= -2
$][$
&quad ((-9) : 3) dot (45 + (-46))\
&= (-3) dot (-1)\
&= 3
$][$
&quad (5 dot (-9)) : (-13 + 28)\
&= -45 : 15\
&= -3
$]
+ #vari[$
&quad 0,25 dot 3 / 25 + (-2 / 5) dot 0,75 : 2,5\
&= 1 / 4 dot 3 / 25 + (-2 / 5) dot 3 / 4 : 5 / 2\
&= 3 / 100 + (-2 / 5) dot 3 / 4 dot 2 / 5\
&= 3 / 100 + (-(2 dot 3 dot 2) / (5 dot 4 dot 5))\
&= 3 / 100 + (-12 / 100) \
&= -9 / 100 = -0,09
$][$
&quad 5 / 8 dot 3,5 : 1,4 + (-1,25) dot 3 / 20 \
&= 5 / 8 dot 7 / 2 : 7 / 5 + (-5 / 4) dot 3 / 20\
&= 5 / 8 dot 7 / 2 dot 5 / 7 + (-(5 dot 3) / (4 dot 20))\
&= (5 dot cancelup(7,1) dot 5) / (8 dot 2 dot canceldown(7,1)) + (-(5 dot 3) / (4 dot 20))\
&= 25 / 16 + (-cancelup(15, 3) / canceldown(80,16)) \
&= cancelup(28,7) / canceldown(16,4) = 1,75
$][$
&quad 0,25 dot 3 / 25 + (-2 / 5) dot 0,75 : 2,5\
&= 1 / 4 dot 3 / 25 + (-2 / 5) dot 3 / 4 : 5 / 2\
&= 3 / 100 + (-2 / 5) dot 3 / 4 dot 2 / 5\
&= 3 / 100 + (-(2 dot 3 dot 2) / (5 dot 4 dot 5))\
&= 3 / 100 + (-12 / 100) \
&= -9 / 100 = -0,09
$]
]
]
#aufgabe(titel: "Zuordnungen erkennen I")[
#operator[Entscheide] für die Zuordnungen, ob sie _proportional_, _antiproportional_ oder _nichts von beidem_ sind. Notiere deine Antwort im Heft und #operator[begründe] deine Entscheidung jeweils.
#unteraufgaben(cols: 2)[
- #vari[
Alter #sym.arrow.r Intelligenz][
Anzahl Handwerker #sym.arrow.r Benötigte Arbeitszeit][
Körpergröße #sym.arrow.r Intelligenz
]
- #vari[
Anzahl Spinnen #sym.arrow.r Anzahl Spinnenbeine][
Umdrehungen des Rades #sym.arrow.r Gefahrene Strecke][
Anzahl Autos #sym.arrow.r Anzahl Autoreifen
]
- #vari[
Anzahl Kinder #sym.arrow.r Anteil vom Geburtstagskuchen][
Dicke eines Buches #sym.arrow.r Anzahl Bücher im Regal][
Anzahl Personen #sym.arrow.r Anteil von einer Pizza
]
- #vari[
Mehl in kg #sym.arrow.r Preis in Euro][
Länge des Schulwegs #sym.arrow.r Zeit für den Schulweg][
Liter Milch #sym.arrow.r Preis in Euro
]
- #vari[
Körpergröße #sym.arrow.r Alter][
Alter #sym.arrow.r Körpergröße][
Intelligenz #sym.arrow.r Schulabschluss
]
- #vari[
Dicke einer Brotscheibe #sym.arrow.r Anzahl an Brotscheiben][
Intelligenz #sym.arrow.r Alter][
Volumen eines Glases #sym.arrow.r Anzahl Gläser, um einen Liter Cola komplett einzuschütten
]
]
#erwartung([entscheidet sich jeweils für eine Zuordnungsart.], 6)
#erwartung([begründet jede Entscheidung nachvollziehbar.], 6)
#loesung[
- #vari[
*Alter #sym.arrow.r Intelligenz* #h(1em) nichts
][
*Anzahl Handwerker #sym.arrow.r Benötigte Arbeitszeit* #h(1em) antiproportional (aber nicht unbegrenzt; mit Begründung auch nichts)
][
*Körpergröße #sym.arrow.r Intelligenz* #h(1em) nichts
]
- #vari[
*Anzahl Spinnen #sym.arrow.r Anzahl Spinnenbeine*: proportional (falls alle Spinnen acht Beine haben)
][
*Umdrehungen des Rades #sym.arrow.r Gefahrene Strecke*: proportional
][
*Anzahl Autos #sym.arrow.r Anzahl Autoreifen Strecke*: proportional
]
- #vari[
*Anzahl Kinder #sym.arrow.r Anteil vom Geburtstagskuchen*: antiproportional (aber irgendwann werden die Stücke zu klein)
][
*Dicke eines Buches #sym.arrow.r Anzahl Bücher im Regal*: antipropotional
][
*Anzahl Personen #sym.arrow.r Anteil von einer Pizza*: antiproportional
]
- #vari[
*Mehl in kg #sym.arrow.r Preis in Euro*: proportional (sofern es keine Rabatte gibt)
][
*Länge des Schulwegs #sym.arrow.r Zeit für den Schulweg*: proportional (mit Begründung auch nichts)
][
*Liter Milch #sym.arrow.r Preis in Euro*: proportional (sofern es keine Rabatte gibt)
]
- #vari[
*Körpergröße #sym.arrow.r Alter*: nichts
][
*Alter #sym.arrow.r Körpergröße*: nichts
][
*Intelligenz #sym.arrow.r Schulabschluss*: nichts
]
- #vari[
*Dicke einer Brotscheibe #sym.arrow.r Anzahl an Brotscheiben*: antiproportional
][
*Intelligenz #sym.arrow.r Alter*: nichts
][
*Volumen eines Glases #sym.arrow.r Anzahl Gläser, um einen Liter Cola komplett einzuschütten*: antiproportional
]
]
]
#aufgabe(titel: "Zuordnungen erkennen II")[
#operator[Entscheide] für die Zuordnungen, ob sie _proportional_ oder _antiproportional_ sind. (Sie sind auf jeden Fall eines von beidem!) Ergänze dann jeweils die fehlenden Werte in den Tabellen.
#unteraufgaben(cols: 2)[
- #vari[#table(
columns: (1cm,) * 7,
rows: 1cm,
align: center + horizon,
fill: (c, r) => if c == 0 {
luma(244)
},
[*x*],
[0,5],
[2],
[3],
[5],
[],
[],
[*y*],
[36],
[],
[6],
[],
[2],
[1],
)][#table(
columns: (1cm,) * 7,
rows: 1cm,
align: center + horizon,
fill: (c, r) => if c == 0 {
luma(244)
},
[*x*],
[0,25],
[2],
[4],
[],
[8],
[],
[*y*],
[56],
[],
[3,5],
[2],
[],
[1],
)][#table(
columns: (1cm,) * 7,
rows: 1cm,
align: center + horizon,
fill: (c, r) => if c == 0 {
luma(244)
},
[*x*],
[0,25],
[2],
[4],
[],
[8],
[],
[*y*],
[56],
[],
[3,5],
[2],
[],
[1],
)]
- #vari[#table(
columns: (1cm,) * 7,
rows: 1cm,
align: center + horizon,
fill: (c, r) => if c == 0 {
luma(244)
},
[*x*],
[3],
[6],
[],
[13],
[15],
[],
[*y*],
[],
[14],
[$56 / 3$],
[],
[35],
[70],
)][#table(
columns: (1cm,) * 7,
rows: 1cm,
align: center + horizon,
fill: (c, r) => if c == 0 {
luma(244)
},
[*x*],
[3],
[4],
[],
[13],
[16],
[],
[*y*],
[25],
[],
[75],
[],
[$400 / 3$],
[175],
)][#table(
columns: (1cm,) * 7,
rows: 1cm,
align: center + horizon,
fill: (c, r) => if c == 0 {
luma(244)
},
[*x*],
[3],
[4],
[],
[13],
[16],
[],
[*y*],
[25],
[],
[75],
[],
[$400 / 3$],
[175],
)]
]
#erwartung([entscheidet sich jeweils für eine Zuordnungsart.], 2)
#erwartung([berechnet jeweils die fehlenden Werte.], 8)
#loesung[
#unteraufgaben(cols: 2)[
- #vari[#table(
columns: (1cm,) * 7,
rows: 1cm,
align: center + horizon,
fill: (c, r) => if c == 0 {
luma(244)
},
[*x*],
[0,5],
[2],
[3],
[5],
[*9*],
[*18*],
[*y*],
[36],
[*9*],
[6],
[*3,6*],
[2],
[1],
)][#table(
columns: (1cm,) * 7,
rows: 1cm,
align: center + horizon,
fill: (c, r) => if c == 0 {
luma(244)
},
[*x*],
[0,25],
[2],
[4],
[*7*],
[8],
[*14*],
[*y*],
[56],
[*7*],
[3,5],
[2],
[*1,75*],
[1],
)][antiproportional#table(columns: (1cm,)*7, rows: 1cm, align: center+horizon, fill:(c,r) => if c == 0 {luma(244)},
[*x*], [0,25], [2], [4], [8], [*7*], [*14*],
[*y*], [56], [*7*], [3,5], [*1,75*], [2], [1]
)]
- #vari[#table(
columns: (1.3cm,) * 7,
rows: 1cm,
align: center + horizon,
fill: (c, r) => if c == 0 {
luma(244)
},
[*x*],
[3],
[6],
[*8*],
[13],
[15],
[*30*],
[*y*],
[*7*],
[14],
[$56 / 3$],
[*30 $1/3$*],
[35],
[70],
)][#table(
columns: (1.3cm,) * 7,
rows: 1cm,
align: center + horizon,
fill: (c, r) => if c == 0 {
luma(244)
},
[*x*],
[3],
[4],
[*9*],
[13],
[16],
[*21*],
[*y*],
[25],
[*33 $1/3$*],
[75],
[*108 $1/3$*],
[$400 / 3$],
[175],
)][proportional#table(columns: (1.3cm,)*7, rows: 1cm, align: center+horizon, fill:(c,r) => if c == 0 {luma(244)},
[*x*], [3], [4], [*9*], [13], [16], [*21*],
[*y*], [25], [*33$1/3$*], [75], [*108$1/3$*], [133$1/3$], [175]
)]
]
]
]
#aufgabe(titel: "Dreisatz")[
#operator[Berechne] falls möglich die Antwort mit Hilfe des Dreisatzes.
#enuma[
+ #vari[
Aus 250 kg Äpfeln erhält man 120 l Apfelsaft. Wie viel Saft erhält man aus 20 kg Äpfeln?
][
12 Brötchen kosten 3,84 €. Wie viele Brötchen kosten 2,24 €?
][
Aus 250 kg Äpfeln erhält man 120 l Apfelsaft. Wie viel Saft erhält man aus 20 kg Äpfeln?
]
+ #vari[
Zwei Maler brauchen 53 Minuten, um ein Zimmer mit 28 m#super[2] zu streichen. Dabei verbrauchen sie 8 l Farbe. Wie lange brauchen 5 Maler für ein Zimmer der gleichen Größe und wie viel Farbe brauchen sie?
][
Vier Freunde fahren in den Urlaub. Sie wechseln sich beim Fahren so ab, dass jeder 93,5 km fährt und sie brauchen 4 Stunden. Wie viele Kilometer müsste jeder fahren, wenn noch zwei Freunde mehr mitkommen? Wie lange brauchen sie dann für den Weg?
][
Drei Bagger brauchen 1,8 Stunden, um eine Grube auszugraben. Sie schichten dabei einen Erdhügel von 2,3 Meter auf. Wie lange brauchen 8 Bagger und wie hoch ist der Erdhügel dann?
]
]
#erwartung([berechnet die Lösung (#vari[9,6 Liter][2,24 €][9,6 Liter]) mit dem Dreisatz.], 3)
#erwartung([berechnet die Lösung (#vari[21,2 Minuten][62 $1/3$ km][0,675 Stunden]) mit dem Dreisatz.], 3)
#erwartung([erkennt, dass sich die zweite Größe nicht ändert.], 1)
#loesung[
+ #vari[$
250 "kg" &arrow.r 120 "liter" \
10 "kg" &arrow.r 4,8 "liter" \
20 "kg" &arrow.r 9,6 "liter" \
$][$
12 &arrow.r 3,84 €\
1 &arrow.r 0,32 €\
7 &arrow.r 2,24 €
$][$
250 "kg" &arrow.r 120 "liter" \
10 "kg" &arrow.r 4,8 "liter" \
20 "kg" &arrow.r 9,6 "liter" \
$]
+ #vari[$
2 &arrow.r 53 "min" \
1 &arrow.r 106 "min" \
5 &arrow.r 21,2 "min" \
$
Die Menge an Farbe ändert sich nicht, da die zu streichende Fläche gleich bleibt.
][$
4 &arrow.r 93,5 "km"\
1 &arrow.r 374 "km"\
6 &arrow.r 62 1 / 3 "km"\
$
Die Fahrzeit ändert sich nicht, da die Fahrtstrecke gleich bleibt.
][$
3 &arrow.r 1,8\
1 &arrow.r 5,4\
8 &arrow.r 0,675\
$
Die Höhe des Berges ändert sich nicht, da die Gleiche Menge an Erde ausgehoben wird.
]
]
]
#aufgabe(titel: "Personenaufzug")[
Bei der Planung von Aufzügen geht man meist von einem Durchschnittsgewicht von 80 kg pro Person aus. Der Aufzug eines Kinos ist für #vari[8][12][9] Personen zugelassen.
Eine Schulklasse mit 30 Kindern, die im Durchschnitt #vari[45][45][48] kg wiegen, möchte mit dem Fahrstuhl in den zweiten Stock fahren. (Die Lehrerinnen nehmen die Treppe.)
Wie oft muss der Fahrstuhl bei Einhaltung der Vorschriften nach oben fahren, bis alle Kinder im zweiten Stock angekommen sind?
#erwartung([findet eine passende Rechnung zur Aufgabe.], 1)
#erwartung([berechnet die Lösung der Aufgabe.], 1)
#erwartung([formuliert einen passenden Antwortsatz.], 1)
#loesung[
Für die Lösung reicht es, die Anzahl der Kinder durch die Anzahl zulässiger Personen pro Fahrt zu teilen und aufzurunden.
#vari[
$ 30 : 8 = 3 "R"6 arrow.r 4 "Fahrten" $
][
$ 30 : 12 = 2 "R"6 arrow.r 4 "Fahrten" $
][
$ 30 : 9 = 3 "R"3 arrow.r 4 "Fahrten" $
]
]
]
|
https://github.com/sartimo/template | https://raw.githubusercontent.com/sartimo/template/main/template.typ | typst | #let bibfile = "quellen.bib"
#let studysubject = "fach"
#let documenttitle = "titel"
#let author = "autor"
#let email = "email"
#let location = "ort"
#let abstract = "beschreibung"
#let today = datetime.today()
#set document(title: documenttitle, author: author)
#set par(justify: true)
#set page(numbering: none, margin: (left: 2in))
#set quote(block: true)
#line(start: (0%, 5%), end: (8.5in, 5%), stroke: (thickness: 2pt))
#align(horizon + left)[
#text(size: 24pt, [#studysubject \ #documenttitle]) \ \
#author \ \
#email \ \
#location, #today.display("[month repr:long] [day], [year]") \ \
#abstract
]
#set heading(numbering: "1.")
#set page(fill: white, margin: (auto))
#pagebreak(weak: true)
#outline(title: "Inhaltsverzeichnis", indent: auto)
#pagebreak(weak: true)
#set page(
numbering: "1",
header: context {
if counter(page).get().first() > 1 [
#documenttitle
#h(1fr)
#author
]
},
footer: context {
align(center, ("Seite " + str(counter(page).get().first())))
})
#counter(page).update(1)
// Content Starts here
= First title
#lorem(100) @WebsiteReference
== Subtitle
=== Sub subject
==== Sub sub subject
= Simple equation
$ x = (2pi*d) / 10 $
== Footnotes
Check the docs for more details.
#footnote[https://typst.app/docs]
== Quotes
#quote(attribution: [Plato], "... ἔοικα γοῦν τούτου γε σμικρῷ τινι αὐτῷ τούτῳ σοφώτερος εἶναι, ὅτιἃ μὴ οἶδα οὐδὲ οἴομαι εἰδέναι.")
== SVG Drawings with Captions
#lorem(100) @Meier2020
#figure(
supplement: "Abbildung",
image("image.svg", width: 20%),
caption: "imageCaptionHere",
)
= Glossar
Begriff: asasasas
\ Begriff2: asasasasasa
#pagebreak(weak: true)
#bibliography(bibfile, title: "Quellenverzeichnis", full: true)
#outline(target: figure.where(kind: image), title: "Abbildungsverzeichnis", indent: auto)
|
|
https://github.com/GuTaoZi/SUSTech-thesis-typst | https://raw.githubusercontent.com/GuTaoZi/SUSTech-thesis-typst/main/template/decl_zh.typ | typst | MIT License | #import "../utils/style.typ" : *
#let decl_zh(
anonymous: false
) = {
if anonymous{
return
}
set align(center)
text("诚信承诺书",size: FSIZE.二号,font: FONTS.黑体, weight: "bold")
set align(left)
set text(size: FSIZE.四号,font: FONTS.宋体)
par(first-line-indent: 2em)[
\
\
1\. 本人郑重承诺所呈交的毕业设计(论文),是在导师的指导下,独立进行研究工作所取得的成果,所有数据、图片资料均真实可靠。
2\. 除文中已经注明引用的内容外,本论文不包含任何其他人或集体已经发表或撰写过的作品或成果。对本论文的研究作出重要贡献的个人和集体,均已在文中以明确的方式标明。
3\. 本人承诺在毕业论文(设计)选题和研究内容过程中没有抄袭他人研究成果和伪造相关数据等行为。
4\. 在毕业论文(设计)中对侵犯任何方面知识产权的行为,由本人承担相应的法律责任。
\
\
\
\
]
align(right)[
#block(width: 11em)[
#align(left)[
#text("作者签名:")
\
#text("________年____月____日")
]
]
]
} |
https://github.com/azduha/akordy | https://raw.githubusercontent.com/azduha/akordy/main/template.typ | typst | #let removeDiacritics(str) = {
str
.replace(regex("[\u0041\u24B6\uFF21\u00C0\u00C1\u00C2\u1EA6\u1EA4\u1EAA\u1EA8\u00C3\u0100\u0102\u1EB0\u1EAE\u1EB4\u1EB2\u0226\u01E0\u00C4\u01DE\u1EA2\u00C5\u01FA\u01CD\u0200\u0202\u1EA0\u1EAC\u1EB6\u1E00\u0104\u023A\u2C6F]"), "A")
.replace(regex("[\uA732]"), "AA")
.replace(regex("[\u00C6\u01FC\u01E2]"), "AE")
.replace(regex("[\uA734]"), "AO")
.replace(regex("[\uA736]"), "AU")
.replace(regex("[\uA738\uA73A]"), "AV")
.replace(regex("[\uA73C]"), "AY")
.replace(regex("[\u0042\u24B7\uFF22\u1E02\u1E04\u1E06\u0243\u0182\u0181]"), "B")
.replace(regex("[\u0043\u24B8\uFF23\u0106\u0108\u010A\u010C\u00C7\u1E08\u0187\u023B\uA73E]"), "C")
.replace(regex("[\u0044\u24B9\uFF24\u1E0A\u010E\u1E0C\u1E10\u1E12\u1E0E\u0110\u018B\u018A\u0189\uA779]"), "D")
.replace(regex("[\u01F1\u01C4]"), "DZ")
.replace(regex("[\u01F2\u01C5]"), "Dz")
.replace(regex("[\u0045\u24BA\uFF25\u00C8\u00C9\u00CA\u1EC0\u1EBE\u1EC4\u1EC2\u1EBC\u0112\u1E14\u1E16\u0114\u0116\u00CB\u1EBA\u011A\u0204\u0206\u1EB8\u1EC6\u0228\u1E1C\u0118\u1E18\u1E1A\u0190\u018E]"), "E")
.replace(regex("[\u0046\u24BB\uFF26\u1E1E\u0191\uA77B]"), "F")
.replace(regex("[\u0047\u24BC\uFF27\u01F4\u011C\u1E20\u011E\u0120\u01E6\u0122\u01E4\u0193\uA7A0\uA77D\uA77E]"), "G")
.replace(regex("[\u0048\u24BD\uFF28\u0124\u1E22\u1E26\u021E\u1E24\u1E28\u1E2A\u0126\u2C67\u2C75\uA78D]"), "H")
.replace(regex("[\u0049\u24BE\uFF29\u00CC\u00CD\u00CE\u0128\u012A\u012C\u0130\u00CF\u1E2E\u1EC8\u01CF\u0208\u020A\u1ECA\u012E\u1E2C\u0197]"), "I")
.replace(regex("[\u004A\u24BF\uFF2A\u0134\u0248]"), "J")
.replace(regex("[\u004B\u24C0\uFF2B\u1E30\u01E8\u1E32\u0136\u1E34\u0198\u2C69\uA740\uA742\uA744\uA7A2]"), "K")
.replace(regex("[\u004C\u24C1\uFF2C\u013F\u0139\u013D\u1E36\u1E38\u013B\u1E3C\u1E3A\u0141\u023D\u2C62\u2C60\uA748\uA746\uA780]"), "L")
.replace(regex("[\u01C7]"), "LJ")
.replace(regex("[\u01C8]"), "Lj")
.replace(regex("[\u004D\u24C2\uFF2D\u1E3E\u1E40\u1E42\u2C6E\u019C]"), "M")
.replace(regex("[\u004E\u24C3\uFF2E\u01F8\u0143\u00D1\u1E44\u0147\u1E46\u0145\u1E4A\u1E48\u0220\u019D\uA790\uA7A4]"), "N")
.replace(regex("[\u01CA]"), "NJ")
.replace(regex("[\u01CB]"), "Nj")
.replace(regex("[\u004F\u24C4\uFF2F\u00D2\u00D3\u00D4\u1ED2\u1ED0\u1ED6\u1ED4\u00D5\u1E4C\u022C\u1E4E\u014C\u1E50\u1E52\u014E\u022E\u0230\u00D6\u022A\u1ECE\u0150\u01D1\u020C\u020E\u01A0\u1EDC\u1EDA\u1EE0\u1EDE\u1EE2\u1ECC\u1ED8\u01EA\u01EC\u00D8\u01FE\u0186\u019F\uA74A\uA74C]"), "O")
.replace(regex("[\u01A2]"), "OI")
.replace(regex("[\uA74E]"), "OO")
.replace(regex("[\u0222]"), "OU")
.replace(regex("[\u0050\u24C5\uFF30\u1E54\u1E56\u01A4\u2C63\uA750\uA752\uA754]"), "P")
.replace(regex("[\u0051\u24C6\uFF31\uA756\uA758\u024A]"), "Q")
.replace(regex("[\u0052\u24C7\uFF32\u0154\u1E58\u0158\u0210\u0212\u1E5A\u1E5C\u0156\u1E5E\u024C\u2C64\uA75A\uA7A6\uA782]"), "R")
.replace(regex("[\u0053\u24C8\uFF33\u1E9E\u015A\u1E64\u015C\u1E60\u0160\u1E66\u1E62\u1E68\u0218\u015E\u2C7E\uA7A8\uA784]"), "S")
.replace(regex("[\u0054\u24C9\uFF34\u1E6A\u0164\u1E6C\u021A\u0162\u1E70\u1E6E\u0166\u01AC\u01AE\u023E\uA786]"), "T")
.replace(regex("[\uA728]"), "TZ")
.replace(regex("[\u0055\u24CA\uFF35\u00D9\u00DA\u00DB\u0168\u1E78\u016A\u1E7A\u016C\u00DC\u01DB\u01D7\u01D5\u01D9\u1EE6\u016E\u0170\u01D3\u0214\u0216\u01AF\u1EEA\u1EE8\u1EEE\u1EEC\u1EF0\u1EE4\u1E72\u0172\u1E76\u1E74\u0244]"), "U")
.replace(regex("[\u0056\u24CB\uFF36\u1E7C\u1E7E\u01B2\uA75E\u0245]"), "V")
.replace(regex("[\uA760]"), "VY")
.replace(regex("[\u0057\u24CC\uFF37\u1E80\u1E82\u0174\u1E86\u1E84\u1E88\u2C72]"), "W")
.replace(regex("[\u0058\u24CD\uFF38\u1E8A\u1E8C]"), "X")
.replace(regex("[\u0059\u24CE\uFF39\u1EF2\u00DD\u0176\u1EF8\u0232\u1E8E\u0178\u1EF6\u1EF4\u01B3\u024E\u1EFE]"), "Y")
.replace(regex("[\u005A\u24CF\uFF3A\u0179\u1E90\u017B\u017D\u1E92\u1E94\u01B5\u0224\u2C7F\u2C6B\uA762]"), "Z")
.replace(regex("[\u0061\u24D0\uFF41\u1E9A\u00E0\u00E1\u00E2\u1EA7\u1EA5\u1EAB\u1EA9\u00E3\u0101\u0103\u1EB1\u1EAF\u1EB5\u1EB3\u0227\u01E1\u00E4\u01DF\u1EA3\u00E5\u01FB\u01CE\u0201\u0203\u1EA1\u1EAD\u1EB7\u1E01\u0105\u2C65\u0250]"), "a")
.replace(regex("[\uA733]"), "aa")
.replace(regex("[\u00E6\u01FD\u01E3]"), "ae")
.replace(regex("[\uA735]"), "ao")
.replace(regex("[\uA737]"), "au")
.replace(regex("[\uA739\uA73B]"), "av")
.replace(regex("[\uA73D]"), "ay")
.replace(regex("[\u0062\u24D1\uFF42\u1E03\u1E05\u1E07\u0180\u0183\u0253]"), "b")
.replace(regex("[\u0063\u24D2\uFF43\u0107\u0109\u010B\u010D\u00E7\u1E09\u0188\u023C\uA73F\u2184]"), "c")
.replace(regex("[\u0064\u24D3\uFF44\u1E0B\u010F\u1E0D\u1E11\u1E13\u1E0F\u0111\u018C\u0256\u0257\uA77A]"), "d")
.replace(regex("[\u01F3\u01C6]"), "dz")
.replace(regex("[\u0065\u24D4\uFF45\u00E8\u00E9\u00EA\u1EC1\u1EBF\u1EC5\u1EC3\u1EBD\u0113\u1E15\u1E17\u0115\u0117\u00EB\u1EBB\u011B\u0205\u0207\u1EB9\u1EC7\u0229\u1E1D\u0119\u1E19\u1E1B\u0247\u025B\u01DD]"), "e")
.replace(regex("[\u0066\u24D5\uFF46\u1E1F\u0192\uA77C]"), "f")
.replace(regex("[\u0067\u24D6\uFF47\u01F5\u011D\u1E21\u011F\u0121\u01E7\u0123\u01E5\u0260\uA7A1\u1D79\uA77F]"), "g")
}
#let song(
title: "",
artist: "",
sections,
) = {
context({
let letter = removeDiacritics(title).at(0)
let letterId = (letter.to-unicode() - "A".to-unicode());
if letterId < 0 {
letterId = -1
letter = "#"
}
let isR = calc.rem(here().page(), 2)
let alignm = top + right
let offsetX = page.margin
let radii = (
top-left: 1em, bottom-left: 1em
)
if (isR == 0) {
alignm = top + left
offsetX = -page.margin
radii = (
top-right: 1em, bottom-right: 1em
)
}
let clr = rgb(color.hsl((letterId / 26) * 360deg, 55%, 45%))
let clrLight = rgb(color.hsl((letterId / 26) * 360deg, 55%, 70%))
place(
alignm,
box(
fill: clr,
radius: radii,
width: 2em,
height: 3.2em,
align(
center + horizon,
text(
size: 1.5em,
fill: white,
weight: "bold",
letter
)
)
),
dx: offsetX,
dy: 1em + (letterId * 28pt),
)
text(fill: clr, heading(title, level: 1))
text(artist, size: 12pt, weight: "bold", fill: clrLight)
v(1em)
columns(1, {
// Check if sections is an array or content
if (type(sections) == array) {
for s in sections {
s
}
} else {
sections
}
})
})
}
#let songSection(
name: "",
body,
) = {
table(
columns: (7%, 93%),
inset: 0em,
align: top,
stroke: none,
text(name, weight: "bold"), {
// Check if body is an array or content
if (type(body) == array) {
for s in body {
s
}
} else {
body
}
}
)
v(0.7em)
}
#let chord(value) = {
context({
let res = query(selector(heading).before(here()))
let lastHeading = res.at(-1)
let shift = 0pt
if (
lastHeading.level == 10 and
calc.abs(here().position().y - lastHeading.location().position().y) < 1em.to-absolute()
) {
let lastX = lastHeading.location().position().x + measure(lastHeading).width + 0.3em
let currentX = here().position().x
shift = calc.max(0em.to-absolute(), (lastX - currentX).to-absolute())
}
box(width: shift, height: 1.6em,
text(
weight: "bold", size: 0.9em, {
table(
columns: (shift, 20pt),
gutter: 0pt,
inset: 0pt,
stroke: none,
"",
heading(level:10, {
text(value)
})
)
}
)
)
// super(text(weight: "bold", size: 1.5em, value))
})
}
#let songbook(
title: "",
subtitle: "",
author: "",
songs: ()
) = {
// Set the document's basic properties.
set document(author: author, title: title)
// Set body font family.
set text(lang: "cs", 12pt)
show heading: it => {
if (it.level < 10) {
text(it.body, weight: "bold", size: 18pt)
v(0em)
} else {
it
}
}
set page(
margin: (
top: 2cm,
bottom: 2cm,
left: 2cm,
right: 2cm
),
paper: "a4",
)
place(
dx: -100%,
box(width: 300%, {
align(right, image(fit: "contain", width: 200%, height: 6em, "media/titlebar.png"))
v(16em)
align(center, text(size: 4em, weight: "bold", upper(title)))
v(-2em)
align(center, text(size: 3em, weight: "bold", upper(subtitle)))
v(16em)
align(left, image(fit: "contain", width: 200%, height: 6em, "media/titlebar.png"))
})
)
pagebreak()
// Set styles
set page(
margin: (
top: 2.5cm,
bottom: 2cm,
left: 2cm,
right: 2cm
),
paper: "a4",
header: {
place(top + right, dy: 4em, text(fill: rgb("#999") , weight: "bold", upper(title)))
},
numbering: "1"
)
set par(justify: false)
v(-0.5em)
outline(target: heading.where(level: 1), title: [
Obsah
#v(0.5em)
])
set page(
margin: (
top: 2cm,
bottom: 2cm,
left: 2cm,
right: 2cm
)
)
let find-child(elem, tag) = {
elem.children
.find(e => "tag" in e and e.tag == tag)
}
// Load songs and render them.
let songs = songs.map(file => {
xml(file).first()
}).map(xml => {
(
title: find-child(xml, "title").children.first(),
noDiacriticsTitle: removeDiacritics(find-child(xml, "title").children.first()),
artist: find-child(xml, "artist").children.first(),
sections: find-child(xml, "sections").children.filter(e => "tag" in e and e.tag == "section")
)
}).sorted(key: object => { object.noDiacriticsTitle }).map(contents => {
pagebreak()
song(
title: contents.title,
artist: contents.artist,
{
contents.sections.map(section => {
let name = ""
if ("name" in section.attrs) {
name = section.attrs.name
}
let first = section.children.remove(0)
first = first.slice(1)
section.children.insert(0, first)
let body = section.children.map(child => {
if ("tag" in child and child.tag == "chord") {
chord(child.attrs.value)
} else {
child.split("\n").map(row => row.trim(regex("\s\s"))).join("\n")
}
})
songSection(name: name, body)
})
}
)
})
for s in songs {
s
}
} |
|
https://github.com/HarryLuoo/sp24 | https://raw.githubusercontent.com/HarryLuoo/sp24/main/math321/hw11.typ | typst | = HW 11 <NAME> <EMAIL>\
\
+ recall stokes theorem $integral.double_(S) (nabla times arrow(F)) dot arrow(n) dif S= integral.cont_(C) arrow(F) dot dif arrow(r)$.\ Let the surface bound by $C$ be a simple disk $x^2+y^2 <=4, z=7$. Unit normal vector of this surface is $arrow(n) = (0,0,1) $ \
$
nabla times arrow(F) = det display(mat(
i,j,k;
(diff )/(diff x) ,(diff )/(diff y) ,(diff )/(diff z);
3x ln(z), 2y z^2, sqrt(x y +e^(x) )))
= display(mat((x)/(2sqrt(x y + e^(x) ) )- 4 y z;(3x)/(z)- (y+e^x )/(2sqrt(x y + e^x) );0))
$
Thus, $(nabla times arrow(F)) dot arrow(n) = 0$.
This implies that $ integral.double_(S) (nabla times arrow(F)) dot arrow(n) dif S= 0$ \
#rect(inset: 8pt)[Thus the result of the given line integral is 0]
+ Recall stokes' theorem, $
integral_(C) arrow(F) dot dif arrow(r) = integral.double_(S) "curl"(arrow(F)) dot arrow(n) dif A = integral.double_(S) "curl" (arrow(F)) dot hat(n) dif S
$ for $A$ s.t. $dif arrow(S) = norm(arrow(r)_(u) times arrow(r)_(v)) dif A$ , $A$ being the projection of $S$ onto the ${u,v}$ plane.
Choose S as the triangle with vertices $(1,0,0),(0,1,0),(0,0,1)$ as suggested, and S follows the equation $x+y+z=1$.
Normal vector to S is $arrow(n)= arrow(r)_(x) times arrow(r)_(y) = (1,1,1) $ Unit normal vector to S is $hat(n) = (1/sqrt(3) , 1/sqrt(3) , 1/sqrt(3) )$
$
nabla times arrow(F) = det display(mat(i,j,k; (diff )/(diff x) ,(diff )/(diff y) ,(diff )/(diff z); x+y^2,y+z^2,z+x^2)) = display(mat(-2z;-2x;-2y))
$
Thus, $(nabla times arrow(F)) dot arrow(n) = -2(x+y+z)$.
$
integral.double_(S) (nabla times arrow(F)) dot arrow(n) dif A
&= -2integral.double_(S) x+y+z dif A \
& = -2integral.double_(S) x+y+1-x-y dif A \
& = -2integral.double_(S) 1 dif A \
& = -2 times "Area: projection of 3d triangle on the xy plane" \
& = -2 times 1/2 \
& = -1
$
Alternatively, we can find this without doing the projection of S onto the $x,y$ plane:
$(nabla times arrow(F)) dot hat(n) = -2/(sqrt(3)) (x+y+z)$
$
integral.double_(S) "curl"(arrow(F)) dot hat(n) dif S &= integral.double_(S) -2/(sqrt(3)) (x+y+z) dif S \
& = -2/(sqrt(3)) integral.double_(S) (x+y + 1 -x -y) dif S \
& = -2/(sqrt(3)) integral.double_(S) 1 dif S \
& = -2/(sqrt(3)) * "Area: 3d triangle" \
& = -2/(sqrt(3)) dot (1/2 * norm( (1,0,-1) times (-1,1,0)) ) \
& = -1
$
+ #rect($
"Re"(z) = sqrt(2); quad "Im" = -pi
$ )
+
(a) $ (2+i)+(sqrt(3)+8i ) = #rect(inset: 8pt)[ $(2+sqrt(3)) +9 i$] $ \
(b) $ (3-6-6i) =
#rect(inset: 8pt)[
$ display( (-3-6i))$
]
$\
(c) $ 16 +2i -24i -3 i ^2 =
#rect(inset: 8pt)[
$ display( (19 -22i))$
]
$
#line(length: 100%)
+
#figure(
grid(
columns: 2,
gutter: 1mm,
rect(inset: 8pt)[
$ display( abs(z) = sqrt((-2)^2+3^2) = sqrt(13) ) $
],image("assets/2024-04-16-16-51-03.png", width: 70%)
))
//6
+ recall triangle inequality $|z_1+z_2| <= |z_1|+|z_2|$.
$
abs(3 + cos(5)i) <= |3|+|cos(5)i|=3+|cos(5)| <= 4\
abs(3 + cos(5)i) = sqrt(3^2+cos^2(5)) >= sqrt(9-1) = sqrt(8) >=2 \
$ #rect[therefore $2<=abs(3 + cos(5)i)<= 4$]
+ #rect(inset: 8pt)[
$ display( z^* = 3-8i)$
]
+ (a) $
((1-i)(1-i))/((1-i)(1+i)) = (1-2i-1)/(2) =
#rect(inset: 8pt)[
$ display( 0+i(-1))$
]
$
(b) $
((1+i)(1-sqrt(2)i ))/((1+sqrt(2)i)(1-sqrt(2)i ) ) = (1-i sqrt(2) +i+sqrt(2) )/(3) = (1+sqrt(2)+(1-sqrt(2) )i )/(3)
#rect(inset: 8pt)[
$ display( = (1+sqrt(2) )/(3) + i (1-sqrt(2) )/(3))$
]
$
(c) $ -i -1 -4 =
#rect(inset: 8pt)[
$ display( -5 +i(-1))$
]
$
+ let $z = a + b i; w = c + d i$. It follows that $
(z w)^* &= (a c - b d) - i (a d + b c) \
z^* w^* &= (a - b i)(c - d i) = (a c - b d) - i (a d + b c) \ &
#rect(inset: 8pt)[
$ display( => (z w)^*=z^* w^*)$
]
$
|
|
https://github.com/weeebdev/cv | https://raw.githubusercontent.com/weeebdev/cv/main/modules/professional.typ | typst | Apache License 2.0 | #import "../brilliant-CV/template.typ": *
#cvSection("Professional Experience")
#cvEntry(
title: [Teaching Assistant],
society: [Nazarbayev University],
logo: "../src/logos/xyz_corp.png",
date: [Apr 2023 - Dec 2023],
location: [Astana, Kazakhstan],
description: list(
[Assisted with teaching and grading for undergraduate courses in CSCI 111 Web Development course, supervised student projects and provided feedback on assignments],
),
)
#cvEntry(
title: [Language Consultant],
society: [what3words],
logo: "../src/logos/abc_company.png",
date: [Jun 2023 - Aug 2023],
location: [London, UK],
description: list(
[Assisted with translation and localization of the what3words app into Kazakh language, provided feedback on language-specific issues and cultural nuances],
),
)
#cvEntry(
title: [Software Engineer],
society: [DAR Tech],
logo: "../src/logos/pqr_corp.png",
date: [Jan 2021 - Apr 2023],
location: [Almaty, Kazakhstan],
description: list(
[Developed and supported communication system called "Mattermost" on all platforms: Web, Desktop, Android, IOS],
[Developed PMS system like Jira and Trello with BPM capabilities],
[Setup pipelines for CI/CD across all projects],
[Developed inner tools for the company],
[Mentored young developers]
),
tags: ("Nest", "Angular", "React")
)
#cvEntry(
title: [Go Developer Apprentice],
society: [JumysBar, Halyk Bank],
logo: "../src/logos/pqr_corp.png",
date: [Sep 2021 - Jan 2022],
location: [Almaty, Kazakhstan],
description: list(
[Developed a microservice for the company],
),
)
#cvEntry(
title: [Information Security Intern],
society: [Beeline],
logo: "../src/logos/pqr_corp.png",
date: [Jun 2020 - Aug 2020],
location: [Almaty, Kazakhstan],
description: list(
[Built an experimental polygon for pentesting],
[Developed a web server for pentesting]
),
)
#cvEntry(
title: [Frontend Developer Intern],
society: [ONE Technologies],
logo: "../src/logos/pqr_corp.png",
date: [Jun 2020 - Aug 2020],
location: [Almaty, Kazakhstan],
description: list(
[Developed lab.one.kz as a final project, the platform for finding internships],
),
)
#cvEntry(
title: [System Administrator Intern],
society: [IT Support Group],
logo: "../src/logos/pqr_corp.png",
date: [May 2020 - Jun 2020],
location: [Almaty, Kazakhstan],
description: list(
[Exchanged data between branches of the company with a help of 1C v8.3],
[Maintained office computers and factory servers],
),
)
#cvEntry(
title: [Teaching Assistant],
society: [Suleyman Demirel University],
logo: "../src/logos/pqr_corp.png",
date: [Oct 2018 - May 2019],
location: [Almaty, Kazakhstan],
description: list(
[Assisted in Information and Communications Technologies practice lessons],
[Assisted in Linear Algebra practice lessons],
[Assisted in Fundamentals of Information Systems practice lessons],
),
)
|
https://github.com/typst/packages | https://raw.githubusercontent.com/typst/packages/main/packages/preview/polytonoi/0.1.0/polytonoi.typ | typst | Apache License 2.0 | // assigns a Roman character to a code point representing its Greek equivalent
// anything not in this list (and not handled elsewhere) will be rendered literally
#let letterDictionary = (
// lower-case letters
a: 0x03B1,
b: 0x03B2,
g: 0x03B3,
d: 0x03B4,
e: 0x03B5,
z: 0x03B6,
h: 0x03B7,
q: 0x03B8,
i: 0x03B9,
k: 0x03BA,
l: 0x03BB,
m: 0x03BC,
n: 0x03BD,
// ksi is handled in the function
o: 0x03BF,
p: 0x03C0,
r: 0x03C1,
// sigma is handled in the function
t: 0x03C4,
u: 0x03C5,
f: 0x03C6,
x: 0x03C7,
// psi is handled in the function
w: 0x03C9,
// upper-case letters. Could do this programatically, but that'd actually be more work
A: 0x0391,
B: 0x0392,
G: 0x0393,
D: 0x0394,
E: 0x0395,
Z: 0x0396,
H: 0x0397,
Q: 0x0398,
I: 0x0399,
K: 0x039A,
L: 0x039B,
M: 0x039C,
N: 0x039D,
// ksi is handled in the function
O: 0x039F,
P: 0x03A0,
R: 0x03A1,
S: 0x03A3, // no capital final sigma, so can just render it normally
T: 0x03A4,
U: 0x03A5,
F: 0x03A6,
X: 0x03A7,
// psi is handled in the function
W: 0x03A9,
// accent marks, return a combining diacritical (which typist handles properly)
"/": 0x0301,
"\\": 0x0300,
"=": 0x0303,
"|": 0x0345,
":": 0x0308,
// rough breathing mark is handled directly in the function
// punctuation
";": 0x0387, // high dot
"?": 0x037E,
)
#let vowelList = (
"a", "e", "i", "o", "u", "w",
"A", "E", "I", "O", "U", "W"
)
#let ptgk(txt) = {
let i = 0
while i < txt.len() {
let ltr = txt.at(i)
// rough breathing mark
if ltr == "(" and vowelList.contains(txt.at(i + 1)) {
let code = letterDictionary.at(txt.at(i + 1))
let brMark = 0x0314
str.from-unicode(code)
str.from-unicode(brMark)
i = i + 2
// apply smooth breathing mark if previous character is a space or this vowel is the first letter of the string, but not if next character is a vowel
} else if vowelList.contains(ltr) {
let prev
if (i == 0) {
prev = " "
} else {
prev = txt.at(i - 1)
}
let next = txt.at(i + 1, default: "")
if prev == " " and next not in vowelList and next != "(" and next != ")" {
let code = letterDictionary.at(ltr)
let brMark = 0x0313
str.from-unicode(code)
str.from-unicode(brMark)
i = i + 1
} else {
let code = letterDictionary.at(ltr)
str.from-unicode(code)
i = i + 1
}
// allow manual addition of smooth breathing mark (e.g. for diphthongs)
} else if ltr == ")" and vowelList.contains(txt.at(i + 1)) {
let code = letterDictionary.at(txt.at(i + 1))
let brMark = 0x0313
str.from-unicode(code)
str.from-unicode(brMark)
i = i + 2
// combining characters (ksi and psi), plus final vs. non-final sigma
} else if ltr == "k" {
let next = txt.at(i + 1, default: "")
if next == "s" {
str.from-unicode(0x03BE)
i = i + 2
} else {
let code = letterDictionary.at(ltr)
str.from-unicode(code)
i = i + 1
}
} else if ltr == "K" {
let next = txt.at(i + 1, default: "")
if next == "s" or next == "S" {
str.from-unicode(0x039E)
i = i + 2
} else {
let code = letterDictionary.at(ltr)
str.from-unicode(code)
i = i + 1
}
} else if ltr == "p" {
let next = txt.at(i + 1, default: "")
if next == "s" {
str.from-unicode(0x03C8)
i = i + 2
} else {
let code = letterDictionary.at(ltr)
str.from-unicode(code)
i = i + 1
}
} else if ltr == "P" {
let next = txt.at(i + 1, default: "")
if next == "s" or next == "S" {
str.from-unicode(0x03A8)
i = i + 2
} else {
let code = letterDictionary.at(ltr)
str.from-unicode(code)
i = i + 1
}
} else if ltr == "s" { // see if we're at the end of a word, in which case render the final sigma
let next = txt.at(i + 1, default: "")
if next == "." or next == "," or next == " " or next == "?" or next == ";" or next == "" or next == "\n" {
str.from-unicode(0x03C2) // final sigma
i = i + 1
} else {
str.from-unicode(0x03C3)
i = i + 1
}
} else {
let code = letterDictionary.at(ltr, default: -2)
if (code != -2 ) {
str.from-unicode(code)
} else {
ltr
}
i = i + 1
}
}
}
|
https://github.com/Area-53-Robotics/53E-Notebook-Over-Under-2023-2024 | https://raw.githubusercontent.com/Area-53-Robotics/53E-Notebook-Over-Under-2023-2024/giga-notebook/entries/build-intake/entry.typ | typst | Creative Commons Attribution Share Alike 4.0 International | #import "/packages.typ": notebookinator
#import notebookinator: *
#import themes.radial.components: *
#create-body-entry(
title: "Build: Intake",
type: "build",
date: datetime(year: 2023, month: 8, day: 18),
author: "<NAME>",
witness: "<NAME>",
)[
#grid(
columns: (1fr, 1fr),
gutter: 10pt,
[
Once the design for the intake was done we could start building it. We completed
the following steps on the first day of building the intake:
1. We gathered all materials specified by the BOM.
2. We cut the aluminum angles down to size. We cut 4 10 long ones, and 2 15 long
ones.
3. We attached the bearings to each of the angles, 1 on each end.
5. We mounted the angles to the drivetrain with the pillow bearings.
6. We then assembled the axles and spacing. We took the two axles, and inserted
them into the 10 long angles.
7. We slid the spacers, sprockets, and locking collars onto each axle.
8. We mounted the motor cap to its axle.
9. We attached the chain to the inner sprockets to bind the two rollers together.
10. We got started on the bracing, screwing the standoffs together in order to get
them to the required length.
11. We then added collars to the end of the standoffs, and then mounted one collar
to one of the 15 long angles, and the other collar to the other one.
#admonition(type: "note")[
We still need to finish the following things:
- Mount the motor
- Add the rubber bands
- Finish the cross bracing
]
],
[
#image("./day1_iso.jpg")
#image("./day1_top.jpg")
#image("./day1_side.jpg")
],
)
]
#create-body-entry(
title: "Build: Intake",
type: "build",
date: datetime(year: 2023, month: 8, day: 19),
author: "<NAME>",
witness: "Violet Ridge",
)[
#grid(
columns: (1fr, 1fr),
gutter: 10pt,
[
The build today was relatively simple. We completed the following steps:
1. Assembled the other half of cross bracing.
#admonition(
type: "note",
)[
We originally planned to have a flexible standoff used in order to not have to
change the height of the second bracing, but this ended up not being
structurally sound. We mirrored the same bracing we build yesterday, but used
more spacers for the mounting in order to bring it above the first one.
]
2. We added a ziptie to the crossbracing to hold the two halves together.
3. We mounted the motor to the motor cap with rubber bands.
4. We added the rubber bands to the outer sprockets, completing the intake rollers.
5. We ziptied mesh to the bottom of the intake to act as an intake surface.
#admonition(
type: "note",
)[
We decided to hold off on full scale testing of the intake subsystem until our
catapult subsystem is complete. The two systems are too integrated to be able to
test them separately.
]
],
[
#image("./day2_iso.jpg")
#image("./day2_top.jpg")
#image("./day2_front.jpg")
],
)
]
|
https://github.com/optimizerfeb/MathScience | https://raw.githubusercontent.com/optimizerfeb/MathScience/main/셀룰러 오토마타를 이용한 게임 컨텐츠 자동생성.typ | typst | #set text(font: "Noto Serif KR")
#align(center, text(17pt)[
*셀룰러 오토마타를 이용한 게임 컨텐츠 자동생성*
])
#align(right, text(10pt)[
한남대학교 수학과
20172581 김남훈
])
= 1. 게임 컨텐츠 자동생성
게임 속에는 맵, NPC, 퀘스트, 던전 등 다양한 컨텐츠가 존재한다. 이러한 컨텐츠들은 개발자가 직접 만들기도 하지만, 때로는 자동생성을 통해 만들기도 한다. 자동생성으로 만들어진 컨텐츠는 단조로운 패턴 등으로 비판받기도 하지만, 매 플레이시마다 다른 맵을 제공하는 게임에는 자동생성이 사실상 필수라고 할 수 있다.
#figure(
image("images/Minecraft.png"),
caption: [마인크래프트의 모든 맵은 자동생성을 통해 만들어진다.]
)
= 2. 셀룰러 오토마타
*셀룰러 오토마타* 는 게임 컨텐츠, 그중 맵을 자동생성하는데 가장 널리 이용된다. 셀룰러 오토마타를 이용한 맵 제작 방법에 대해 알아보기 전에, 먼저 셀룰러 오토마타의 정의를 알아보자.
*오토마타* 는 상태의 집합 $Q$ 와 입력의 집합 $Sigma$, 입력에 따른 상태 변화를 나타내는 함수 $delta$
$ delta : Q times Sigma arrow.r Q $
와 처음 상태 $q_0$, 최종 상태 $q_omega$ 로 이루어진 수학적 구조 $cal(A) = (Q, Sigma, delta, q_0, q_omega)$ 이다.
*셀룰러 오토마타* 는 주변의 다른 오토마타들의 상태를 입력으로 받는 오토마타이다. 셀룰러 오토마타의 대표적인 예시로, *콘웨이의 생명 게임* 이 있다.
#figure(
image("images/Game of Life.svg", width: 90%),
caption: [콘웨이의 생명 게임\ 각각의 격자가 셀룰러 오토마타이다.]
)
콘웨이의 생명 게임은 다음과 같은 규칙으로 진행된다. 주변에 존재하는 상태 $1$ 의 갯수를 입력이라 할 때
#figure(
table(
columns: (auto, auto, auto, auto, auto),
$delta$, [$0 ~ 1$ 개], [$2$ 개], [$3$ 개], [$4 ~ 8$ 개],
$1$, $0$, $1$, $1$, $0$,
$0$, $0$, $0$, $1$, $0$
),
caption: [생명 게임의 규칙]
)
와 같으며, 실제로 그림에서는 표와 같은 규칙으로 각 격자의 상태가 변화함을 확인할 수 있다.
== 엄밀한 정의
+ $A, B$ 가 집합일 때, $A^B$ 는 $B$ 에서 $A$ 로의 모든 함수의 집합을 나타낸다.
+ $A, B, C$ 가 집합이고 $A subset B$ 이며 $f : A arrow.r C$ 라 할 때, $f bar_B$ 는 모든 $x in B$ 에 대해
$
f(x) = f bar_B (x)
$
인 $B$ 에서 $C$ 로의 함수를 나타낸다.
+ $G$ 가 군, $A$ 가 집합이고 $sigma : G arrow.r A$ 이며 $g in G$ 일 때, $g sigma$ 는, 모든 $h$ 에 대해
$
g sigma(h) = sigma(g^(-1) h)
$
인 $G$ 에서 $A$ 로의 함수를 나타낸다.
$G$ 를 군, $S$ 를 $G$ 의 어떤 유한 부분집합, $Sigma$ 를 오토마타가 가질 수 있는 상태의 집합이라 하자. 그리고 $mu$ 를 $Sigma^S$ 에서 $Sigma$ 로의 임의의 함수(함수를 값으로 받는 함수)라 하자. 이제 $tau$ 를, 다음 성질을 만족하는 $Sigma^G$ 에서 $Sigma^G$ 로의 함수라 하면, $cal(C) = (G, Sigma, tau)$ 를 군 $G$ 와 상태 $Sigma$ 위의 *셀룰러 오토마타* 라고 한다.
$
forall x in Sigma^G, forall g in G\
[tau(x)](g) = mu[(g^(-1)x) bar_S]
$
= 3. 셀룰러 오토마타를 이용한 게임 컨텐츠 자동생성
셀룰러 오토마타를 이용해 게임의 맵을 자동생성하는 두 가지 방법을 알아보자.
=== 다수의 섬으로 이루어진 지형 자동생성
첫번째로, 셀룰러 오토마타를 이용해 랜덤 노이즈로부터 여러개의 섬이 존재하는 맵을 생성하는 방법이다.
#figure(
image("images/Islands.svg"),
caption: [랜덤 노이즈로부터 섬 생성]
)
여기에서는, 각 픽셀은 주변 여덟 픽셀의 색깔을 입력으로 받아, 흰 픽셀이 4개 이상이면 자신의 색을 흰색으로, 3개 이하이면 자신의 색깔을 검정색으로 변경한다. 이것을 11회 반복하여 랜덤 노이즈로부터 섬을 생성할 수 있다.
=== WFC 알고리즘
WFC(Wave Function Collapse) 알고리즘은 비교적 최근인 2016년 발표된 알고리즘으로, 셀룰러 오토마타를 이용해 보다 복잡하고 일관성 있는 맵을 생성하는 알고리즘이다. Wave Function Collapse 라는 이름은 양자역학적 현상인 *파동함수 붕괴* 에서 따온 이름으로, 관측 전까지 파동함수의 형태로 확률로서만 존재하던 각 입자의 상태가 관측 순간 파동함수가 붕괴하여 확정되는 양자역학의 법칙과 유사하여 지어진 이름이다.
셀룰러 오토마타가 가질 수 있는 상태, 즉 타일의 집합 $S$ 와 미리 상태가 정해진 몇 개의 타일이 주어졌을 때, WFC 알고리즘은 상태가 정해진 타일의 주변 좌표들을 *관측* 한다. 주위에 어떤 타일이 있는지에 따라 각 좌표의 타일의 확률 분포가 정해지며, 각 좌표를 관측할 때마다 확률 분포에 따라 각 위치의 타일이 *확정* 된다. 이러한 과정은 맵 위의 모든 좌표에서 타일이 확정될때까지 반복된다.
각 오토마타가 $0$ 과 $1$ 만을 상태로 갖는 위의 방법과 달리, WFC 알고리즘은 다양한 상태를 가질 수 있는 오토마타를 사용하며, 타일이 보다 일관적이도록 배치하기 때문에 다음과 같은 자연스러운 맵을 생성할 수 있다.
#figure(
image("images/wavemap.png"),
caption: [WFC 알고리즘으로 생성한 맵]
)
WFC 알고리즘을 이용해 다음과 같은 전자 회로도 그릴 수 있다.
#figure(
image("images/wavecircuit.png"),
caption: [WFC 알고리즘을 이용해 그린 회로]
)
= 참고문헌
#align(left, text(9pt)[
Ceccherini-Silberstein, Tullio, et al. Cellular Automata and Groups. Springer Berlin Heidelberg, 2010.\
<NAME>., & <NAME>. (Eds.). (2017). Procedural generation in game design. CRC Press.\
<NAME>. (2016). Wave Function Collapse Algorithm (Version 1.0) [Computer software]. https://github.com/mxgmn/WaveFunctionCollapse
]) |
|
https://github.com/Myriad-Dreamin/typst.ts | https://raw.githubusercontent.com/Myriad-Dreamin/typst.ts/main/fuzzers/corpora/layout/transform-layout_01.typ | typst | Apache License 2.0 |
#import "/contrib/templates/std-tests/preset.typ": *
#show: test-page
// Test relative sizing in rotated boxes.
#set page(width: 200pt, height: 200pt)
#set text(size: 32pt)
#let rotated(body) = box(rotate(
90deg,
box(stroke: 0.5pt, height: 20%, clip: true, body)
))
#set rotate(reflow: false)
Hello #rotated[World]!\
#set rotate(reflow: true)
Hello #rotated[World]!
|
https://github.com/Drodt/clever-quotes | https://raw.githubusercontent.com/Drodt/clever-quotes/main/src/clever-quotes.typ | typst | #import "predefined.typ": default-quote-styles, default-quote-aliases, get-default-style
#let quote-style = state("quote-style", "en/US")
#let quote-max-level = state("quote-max-level", 2)
#let quote-level = counter("quote-level")
#let _get-style(s) = {
let sty = s
if type(s) == "string" {
sty = get-default-style(s)
}
if sty == none {
panic("Unknown quotation style: ", s)
}
sty
}
/// Sets up the parameters for the quotation functions.
///
/// Use this function like so:
///
/// ```typ
/// #show: clever-quotes.with(style: "de")
/// ```
///
/// - style (string, dictionary): The quotation style to use.
/// - max-level (integer, none): Maximal level of quote-nesting. `none` disables the limit.
/// - body (content): The content to render.
#let clever-quotes(
style: "en/US",
max-level: 2,
body
) = {
let sty = _get-style(style)
quote-style.update(sty)
quote-max-level.update(max-level)
body
}
/// Put some text in context-sensitive quotes, using the currently active style.
/// If this is used in some other `quote` call and that is a outer quote, the
/// inner call will produce an inner quote. Analagously, if the outer call produced
/// inner quotes, we produce outer quotes.
///
/// - inner (boolean): Whether to start with an inner quote.
/// - style (string, dictionary, auto): The style to use for this quote. If `auto`, it will use the global style.
/// - cite (content, none): Optional citation content at the end of the quote.
/// - body (content): Content inside the quotation marks.
#let quote(inner: false, style: auto, cite: none, body) = {
locate(loc => {
let style = if style == auto {
quote-style.at(loc)
} else {
_get-style(style)
}
let max-level = quote-max-level.at(loc)
let incr = if inner {
quote-level.step() + quote-level.step()
} else {
quote-level.step()
}
let content = quote-level.display(lvl => {
let is-inner = calc.even(lvl)
let (open, close) = if is-inner {
(style.at("inner-open"), style.at("inner-close"))
} else {
(style.at("outer-open"), style.at("outer-close"))
}
let citation = if cite == none {
none
} else {
[ #cite]
}
open + body + close
})
incr + content + quote-level.update(0)
})
}
/// Cites a source and gives a quotation.
///
/// - inner (boolean): Whether to start with an inner quote.
/// - style (string, dictionary, auto): The style to use for this quote. If `auto`, it will use the global style.
/// - cite (content): The citation to be inserted after the quote.
/// - body (content): Content inside the quotation marks.
#let citequote(inner: false, style: auto, cite, body) = quote(inner: inner, style: style, cite: cite, body)
/// Produces a block quote.
///
/// - cite (content, none): Optional citation content at the end of the quote.
/// - inset (length, dictionary): How much to pad the block. A passed length will be used as left-padding.
/// - font-size (length): Font size of the block content.
/// - body (content): Content for the blockquote.
#let blockquote(
cite: none,
inset: 2em,
font-size: 1em,
body
) = {
let inset = if type(inset) == "dictionary" {
inset
} else {
(left: inset)
}
let citation = if cite == none {
none
} else {
[ #cite]
}
set text(size: font-size)
quote-level.display() + block(width: 100%, inset: inset, body + citation) + quote-level.display()
}
/// Produces a block quote with a citation.
///
/// - inset (length, dictionary): How much to pad the block. A passed length will be used as left-padding.
/// - font-size (length): Font size of the block content.
/// - cite (content): Optional citation content at the end of the quote.
/// - body (content): Content for the blockquote.
#let blockcitequote(
inset: 2em,
font-size: 1em,
cite,
body
) = blockquote(cite: cite, inset: inset, font-size: font-size, body)
/// Adds insertion marks (`[]`) around some text in the quote to denote
/// it was added.
///
/// - body (content): The added content in the quote.
#let text-ins(body) = [[#body]]
/// Adds inserted elipsis `[...]` and the inserted content in brackets.
///
/// If the body is `none`, only elipsis are added.
/// - inverted (boolean): If true, inserts the body first, then elipsis.
/// - body (content, none): The content added to the quote.
#let text-elp-ins(inverted: false, body) = if body == none {
text-ins[...]
} else if inverted {
text-ins(body) + text-ins[...]
} else {
text-ins[...] + text-ins(body)
}
/// Adds `[...]` to the text.
#let text-elp = text-elp-ins(none)
/// Outputs `[...]`; the body is not displayed.
///
/// - body (content): The body which was deleted from the quote.
#let text-del(body) = text-elp
|